Knuth's Algorithm X / DLX

JaehyeokSong0·2022년 2월 16일
DLXalgorithm
2

Algorithm

목록 보기
1/1

본 포스트는 기본적으로 이 포스트와 위키피디아 문서 등을 바탕으로 공부한 내용을 최대한 쉽게 풀어서 개인적으로 정리해보고자 작성되었습니다.
충분한 알고리즘 지식이 있다면 앞서 명시된 포스트를 참고하시는 게 더 빠를 수 있습니다!

개요

Knuth's Algorithm X는 Exact Cover 문제를 해결하기 위해 Donald E. Knuth가 제시한 알고리즘이다.

Dancing Links 테크닉을 사용하여 구현한 Algorithm X를 DLX라고 한다.

Exact Cover

집합 U = {1, 2, 3, 4, 5, 6, 7}이고, U의 부분집합 S = {A, B, C, D, E, F}이다.

  • A = {1, 4, 7};
  • B = {1, 4};
  • C = {4, 5, 7};
  • D = {3, 5, 6};
  • E = {2, 3, 6, 7};
  • F = {2, 7};
    라고 할 때, 다음 조건을 만족하는 S의 부분집합을 구하는 문제를 Exact Cover라고 한다.
    1. S를 구성하는 원소들끼리의 교집합은 비어 있어야 한다.
    2. S를 구성하는 원소들끼리의 합집합은 U가 되어야 한다.

즉, A ~ F 집합을 각 원소가 한 번씩만 사용되도록 구성해서 U의 모든 원소가 나타나게 하면 된다.
위의 예시에서는 S = {B, D, F}가 Exact Cover를 만족한다.

Knuth's Algorithm X

앞서 Exact Cover에서 설명했던 예제를 기준으로 Knuth's Algorithm X를 적용해본다.
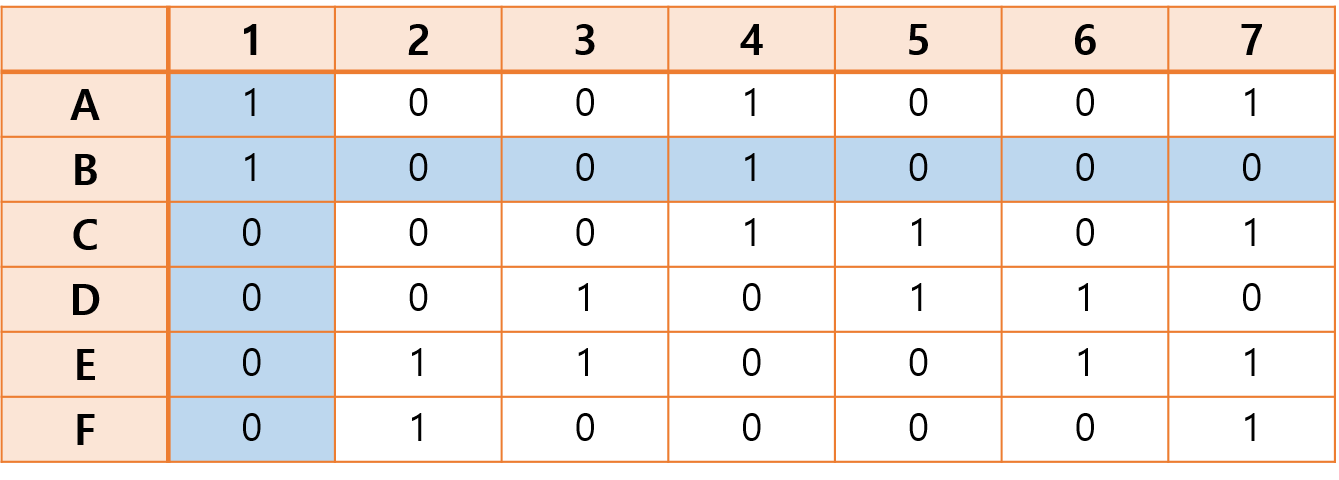
각 집합 A~F가 어떤 원소를 가지고 있다면 1, 그렇지 않다면 0으로 표기하여 행렬을 생성했다.

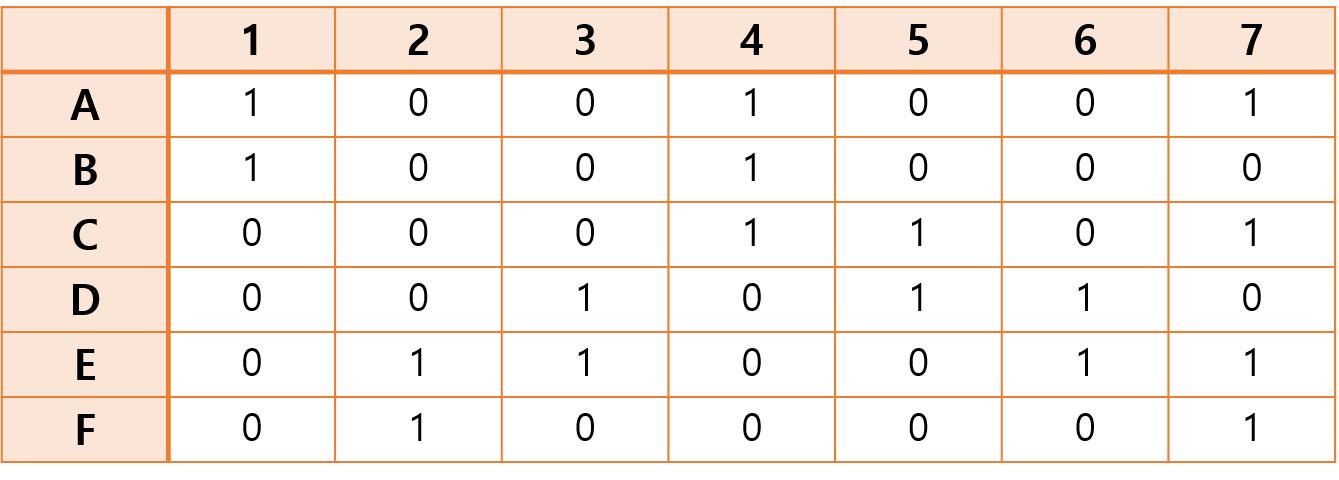
들어가기에 앞서, 알고리즘의 전체적인 흐름은 다음과 같다.

  1. 만약 행렬이 비어있지 않다면, 알고리즘을 계속 진행한다.
  2. 1의 개수가 가장 적은 열을 하나 선택한다. 만약, 1이 하나도 없는 열이 존재한다면 알고리즘이 실패했음을 의미하므로 해당 분기를 종료한다.
  3. 2에서 선택한 열에서 1이 있는 행을 partial solution에 포함 후 제거한다. (nondeterministically)
  4. 3에서 선택한 행에서 1이 속한 열을 모두 제거한다.
  5. 4에서 선택한 열에서 1이 속한 행을 모두 제거한다.
  6. 남은 행렬에 대해서 앞선 과정을 반복한다.

예제 적용

예제에 이를 적용하여 차근차근 이해해보자.

  1. 1의 개수가 가장 적은 열을 하나 선택한다. 만약, 1이 하나도 없는 열이 존재한다면 알고리즘이 실패했음을 의미하므로 해당 분기를 종료한다.

각 열이 가지는 1의 개수는 순서대로 2, 2, 2, 3, 2, 2, 4이다.
따라서 1의 개수가 2개로 가장 적은 1열을 선택한다.

  1. 2에서 선택한 열에서 1이 있는 행을 partial solution에 포함 후 제거한다. (nondeterministically)

1열에서 1이 있는 행은 A행, B행이다.
이 중 A행을 선택하기로 하고, 이를 solution에 포함 후 제거한다.
(현재 solution = { A })

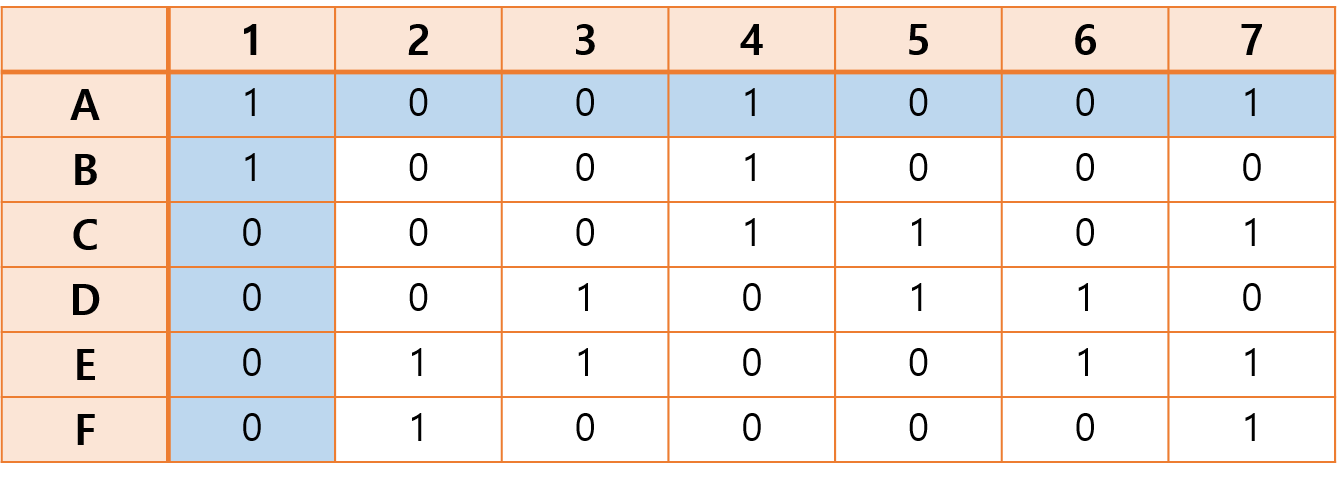
  1. 3에서 선택한 행에서 1이 속한 열을 모두 제거한다.

A행에서 1이 속한 열은 4, 7열이므로 4, 7열을 제거한다.

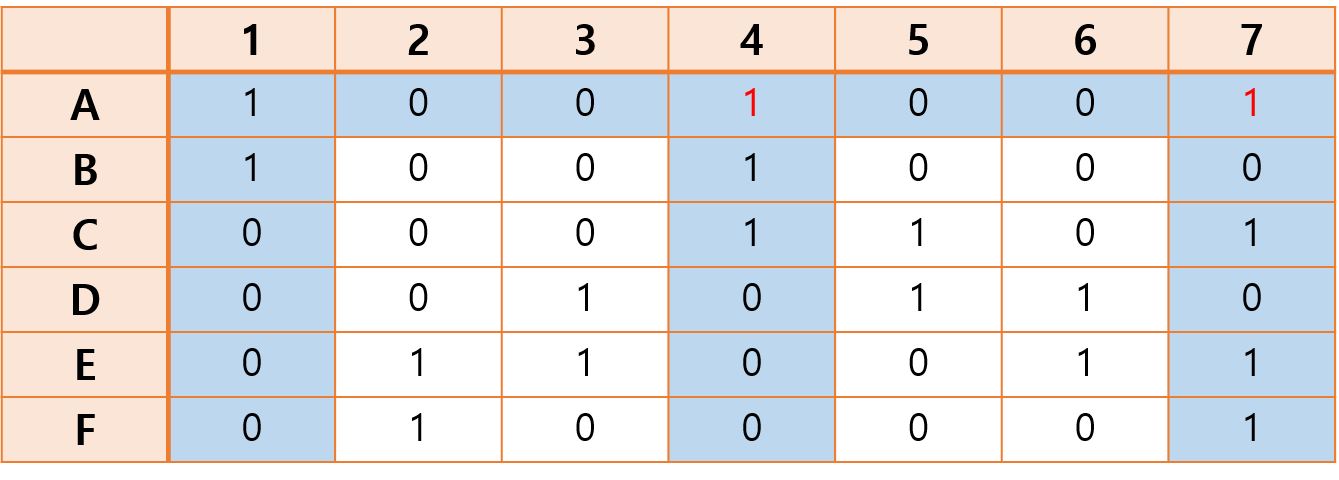
  1. 4에서 선택한 열에서 1이 속한 행을 모두 제거한다.

4열에서 1이 속한 행은 B, C행이고 7열에서 1이 속한 행은 C, E, F행이다.
따라서 B, C, E, F행을 제거한다.

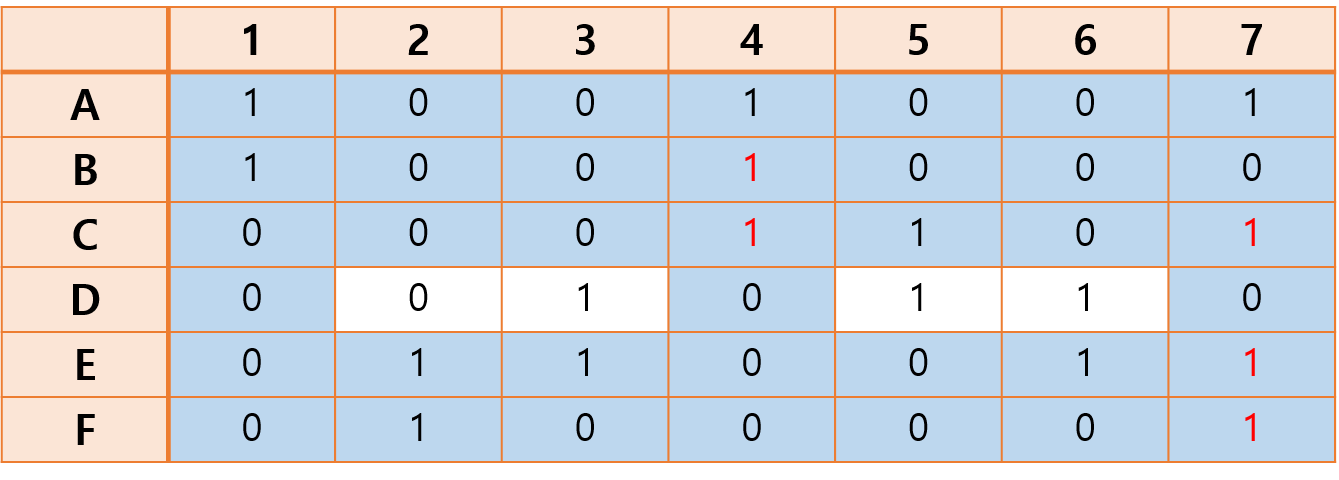
그 결과 남은 행렬은 다음과 같다.

  1. 만약 행렬이 비어있지 않다면, 알고리즘을 계속 진행한다.
  2. 1의 개수가 가장 적은 열을 하나 선택한다. 만약, 1이 하나도 없는 열이 존재한다면 알고리즘이 실패했음을 의미하므로 해당 분기를 종료한다.

남은 행렬은 비어있지 않기 때문에 [과정 1]을 만족한다. 그러나 [과정 2]에서 2열이 1을 하나도 가지고 있지 않아 해당 분기에서의 알고리즘이 실패했음을 알 수 있다.

따라서 앞서 [과정 3]에서 solution에 포함했던 A를 제거하고, 또 다른 분기점이었던 B행에 대해서 같은 알고리즘 과정을 진행한다.
(현재 solution = { B })

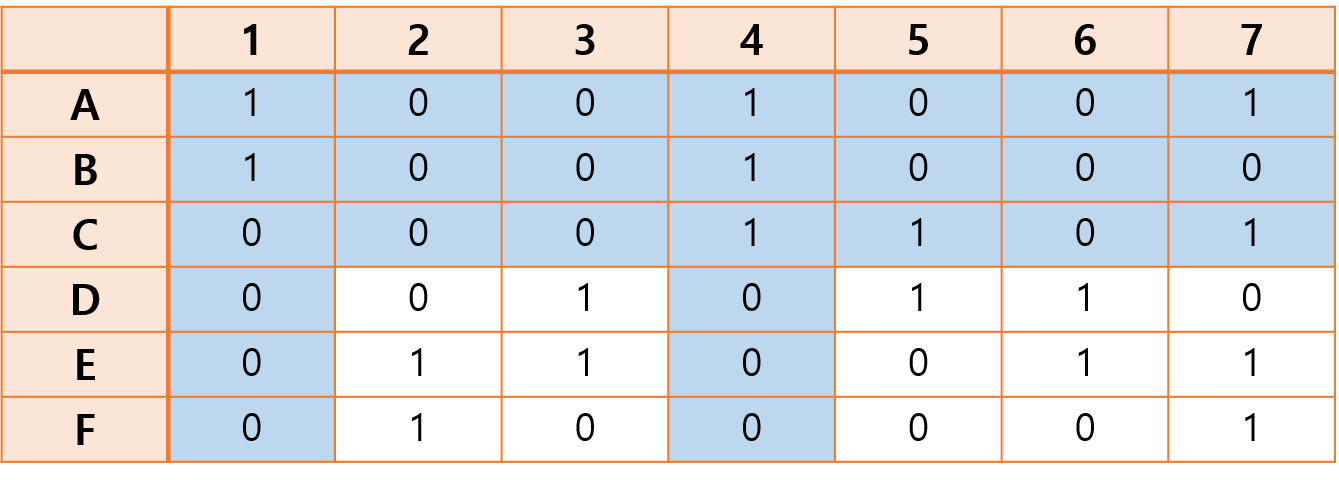
  1. 3에서 선택한 행에서 1이 속한 열을 모두 제거한다.
  2. 4에서 선택한 열에서 1이 속한 행을 모두 제거한다.

[과정 4]에서 4열을 제거하고, [과정 5]에서 A, C행을 제거함으로써 알고리즘을 수행한다.

그 결과 다음과 같은 남은 행렬을 얻을 수 있다.

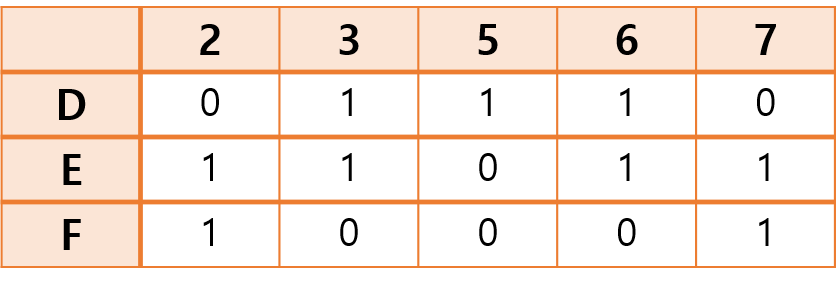
남은 행렬이 비어있지 않고, 모든 열에 적어도 하나의 1이 존재하므로 [과정 1]과 [과정 2]에서의 조건을 모두 만족한다. 따라서 남은 행렬에 대해서 앞선 알고리즘을 계속 수행한다.

위 [과정 3]에서 현재 solution에 D를 추가하여 solution = {B, D}가 된다.

앞선 과정을 통해 위와 같은 남은 행렬을 얻을 수 있다.
이 역시 마찬가지로 [과정 1]과 [과정 2]에서의 조건을 만족하므로 알고리즘을 이어 수행할 수 있다.

결과

이 행렬에 대해 다시 한번 알고리즘을 수행하게 되면(과정 생략) 그 결과로 빈 행렬과 solution = {B, D, F}를 얻을 수 있다. 빈 행렬이 return되었으므로 해당 알고리즘은 성공했다! 이를 통해 문제에서 주어진 Exact Cover를 이루기 위해서는 B, D, F가 필요하다는 사실을 알 수 있다.

Dancing Links는 circular doubly linked list에서 노드를 삽입하고 제거하는 기술이다.

노드의 제거

노드의 제거는 다음과 같이 진행할 수 있다.

x.left.right <- x.right;
x.right.left <- x.left;


x.left.right <- x.right;이 실행된다면, x의 left인 L이 가리키는 right 포인터가 x의 right인 R을 가리키게 된다.
그 결과 L이 X를 가리키던 link가 사라졌다.

같은 방식으로 코드의 둘째 줄을 마저 실행하게 되면, 결과적으로 아래 그림과 같이 X를 가리키는 양 옆 노드의 포인터가 제거되어 X에 접근할 수 없어진다.
이 때 X의 left, right 포인터에는 변화가 없으므로 여전히 각각 L과 R를 가리키고 있다.

노드의 삽입

노드의 삽입은 다음과 같이 진행할 수 있다.

x.left.right <- x;
x.right.left <- x;

사실 노드의 삽입이라기보다는 제거된 노드의 복원restore에 더 가깝다.

앞선 그림에서 X는 여전히 각각 L과 R을 가리키는 left, right 포인터를 가지고 있으므로
x.left.right 는 L의 right포인터이다. (현재 가리키는 대상 : R)
이를 다시 x.left.right <- x; 명령어를 통해 X를 가리키도록 수정한다.

노드의 삽입 과정에서 주의할 점이 있는데, 삭제가 이루어진 역순으로 진행해야 완전한 노드의 복원이 가능하다. 순서가 지켜지지 않는다면 오류가 발생하거나 예기치 못한 상황이 일어날 수 있다.

DLX

이제 Knuth's Algorithm X를 Dancing links 테크닉을 이용하여 구현해보자.
예시는 Donald Knuth의 Dancing Links 논문을 바탕으로 한다.
(출처 : https://arxiv.org/pdf/cs/0011047.pdf)
또한, 구현에 사용된 소스코드는 다음 포스트에서 구했다.
(출처 : http://www.secmem.org/blog/2019/12/15/knuths-algorithm-x/)


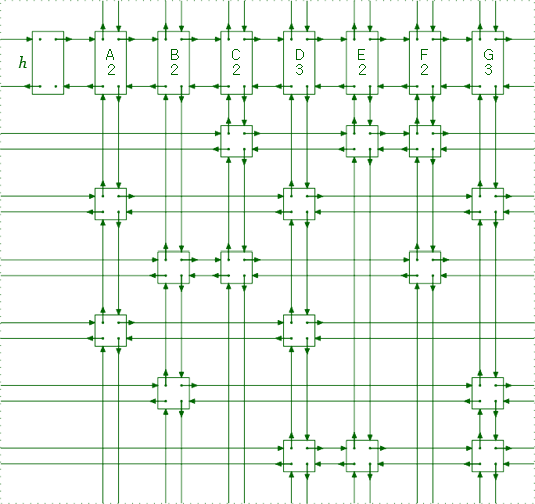
위 그림은 앞선 Exact Cover와 같은 문제에서 사용된 행렬을 2차원 Linked List 형태로 구현한 것이다.
(위에서 들었던 예시와는 다른 예시이니 주의.)

각 집합별 원소는 기존 표에서는 1로 표현되었지만, 여기서는 노드로 구현되어 인접한 노드와 링크를 가진다. 또한 각 column별로 head 노드를 생성하여 column에 현재 속해있는 노드의 개수를 관리한다.

node

DLX를 수행하기 위해 필요한 노드의 구조는 다음과 같이 구현할 수 있다.

struct node
{
	int row;	// 노드의 행 번호. 최종 solution 출력 시 사용
    int size;	// head 노드에서 사용. 현재 column이 가지고 있는 노드(1)의 개수를 저장
    node* col;	// 각 column별 head를 가리키는 포인터
    
    // 인접한 노드를 가리키는 포인터 변수
    node* up;
    node* down;
    node* left;
    node* right;	
}

cover

앞서 algorithm X를 수행할 때 column을 제거했던 작업을 cover라는 함수를 통해 구현하면 다음과 같다.
제거라는 단어를 사용하지만, Dancing links 테크닉을 사용하기 때문에 실제로 노드가 사라지는 것은 아님에 주의하자.

void dlx_cover(node *c) // column head 노드 입력
{
	// dancing links를 통해 c를 가리키는 양 옆의 노드 포인터 제거 (열 제거)
	c->right->left = c->left;
	c->left->right = c->right;
   
    // head로부터 아래 노드로 이동하며 
	for (node* it = c->down; it != c; it = it->down) {
   		// 오른쪽 노드로 이동하며 위 아래 노드 포인터 제거 (행 제거)
		for (node* jt = it->right; jt != it; jt = jt->right) {
			jt->down->up = jt->up;
			jt->up->down = jt->down;
			jt->col->size--; // 제거한 노드의 head의 size 감소
		}
	}
}

이 때 반복문에서 명시된 종료 조건인 it != c;나 jt != it가 성립할 수 있는 이유는 dancing links가 circular linked list 구조 상에서 동작하기 때문이다.
따라서 cover 함수는 column head 노드를 입력받으면 해당 head를 제거하고, 같은 column에 속한 노드들이 속한 행 역시도 제거하는 작업을 수행하게 된다.

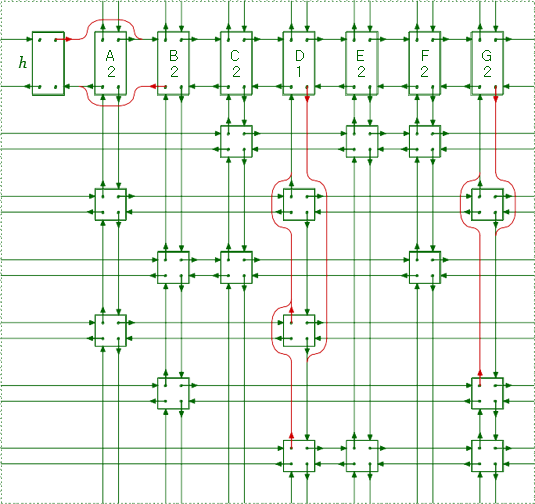
주어진 예시에서 A열을 cover하게 되면 다음과 같은 결과를 얻을 수 있다.

  1. head A 제거
  2. A열에 속한 노드(2, 4행)들에 대해, 같은 행에 속한 노드로 이동하며 위 아래 링크 제거.
    • 2행 : D, G
    • 4행 : D
  3. 결과적으로는 A열과 2, 4행이 제거된 효과를 볼 수 있다.

uncover

uncover는 제거된 노드의 복원이다. cover의 역순으로 수행하면 된다.

void dlx_uncover(node* c) { // column head 노드 입력
    // head로부터 위 노드로 이동하며 
	for (node* it = c->up; it != c; it = it->up) {
       	// 왼쪽 노드로 이동하며 dancing links 통해 위 아래 노드 포인터 복원 (행 복원)
		for (node* jt = it->left; jt != it; jt = jt->left) {
			jt->down->up = jt;
			jt->up->down = jt;
			jt->col->size++;
		}
	}
    // head 노드의 양 옆 포인터 복원 (열 복원)
	c->right->left = c;
	c->left->right = c;
}

search (solve)

최종적으로 구현한 DLX의 코드는 다음과 같다.

bool dlx_search(node* head, int k, vector<int>& solution) {
	if (head->right == head) return 1; // 빈 행렬이면 알고리즘 성공했으므로 종료
    
	node* ptr = nullptr;
	int low = INF; 
    // 가장 작은 size의 column 찾은 후 ptr 포인터로 해당 column head 가리킴
	for (node* it = head->right; it != head; it = it->right) {
		if (it->size < low) {
			if (it->size == 0) return 0; // 노드가 하나도 없는 열이 존재한다면 알고리즘 실패한 것이므로 분기 종료
			low = it->size;
			ptr = it;
		}
	}
    
	dlx_cover(ptr);
    
    // cover된 column head와 같은 열에 속한 노드들에 대해서
	for (node* it = ptr->down; it != ptr; it = it->down) {
		solution.push_back(it->row); // 노드가 속한 행(이미 cover됨)을 solution에 포함
        
        // 해당 행에 속한 노드들의 column head에 대해 cover 수행 (algorithm X의 [과정 4] & [과정 5]에 해당)
		for (node* jt = it->right; jt != it; jt = jt->right) {
			dlx_cover(jt->col);
		}
        
		if (dlx_search(head, k + 1, solution)) return 1; // 알고리즘 성공적으로 수행
		else { // 해당 분기에서 알고리즘 수행 실패
			solution.pop_back(); // 가장 최근에 포함한 solution 원소 제거
            
            // 해당 행에 속한 노드들의 column head에 대해 uncover 수행하여 linked list 구조 복원
			for (node* jt = it->left; jt != it; jt = jt->left) {
				dlx_uncover(jt->col);
			}
		}
	}
	dlx_uncover(ptr); // linked list 구조 복원
	return 0;
}

[부연 설명]
1. 함수에 파라미터로 요구되는 int k는 dfs에서의 depth와 유사하다. dlx_search 함수 호출의 깊이를 나타낸다.
2. 함수가 해당 분기 내에서 성공적으로 수행되는 경우 1을 반환, 그렇지 않다면 0을 반환한다.
if(dlx_search(head, k + 1, solution))에서 현재 분기가 제대로 수행되고 있는지를 검사하며, 0이 반환되었다면 아래의 else 문을 통해 현재 분기를 이전 분기점까지 되돌린다. (백트래킹)
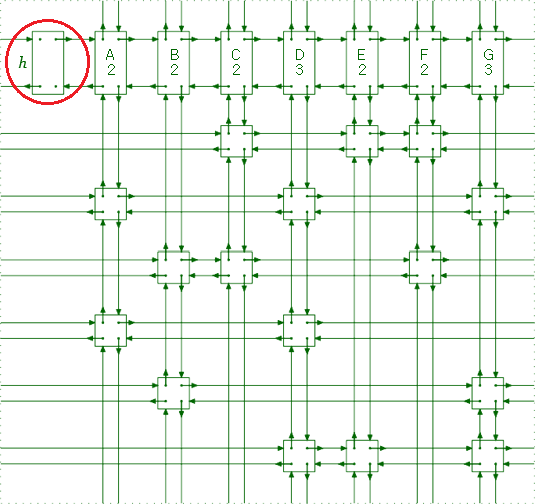
3. 2줄의 if (head->right == head) return 1에서, head->right == head는 빈 행렬을 나타낸다. 이는 아래 그림에서 표시한 base head만 남았기 때문이다.

어디에 사용할까

Exact Cover 문제로 치환될 수 있는 대표적인 유형으로는 펜토미노나 스도쿠가 있다.

스도쿠를 예시로 들어보자.
우선 Column에 들어가야 할 요소를 고려해야 한다.

  1. 스도쿠의 각 칸에는 하나의 숫자밖에 들어갈 수 없다. 이를 위한 81(= 9 * 9)개의 column이 필요하다.
  2. 스도쿠의 각 가로줄, 세로줄, 박스(3 * 3 사각형)에는 1 ~ 9의 숫자가 하나씩만 사용되어야 한다. 이를 위해 243(= 3 * 9 * 9)개의 column이 필요하다.

따라서 324개의 column이 필요하다.

이제 Row에 들어가야 할 요소를 고려한다.

  1. 스도쿠의 각 칸에는 1 ~ 9 사이의 숫자가 하나 들어간다. 따라서 729(= 9 * 9 * 9)개의 row가 필요하다.

만약 (4,5) 위치에 숫자 2가 들어가게 된다면 이는 (4,5,2)로 표현할 수 있을 것이다.

이렇게 고려한 Column과 Row는 간단히 다음과 같은 324 * 729 행렬로 표현할 수 있다.

스도쿠 행렬을 입력받으면서 (4,5) 위치에 2가 들어가게 된다면, 아래 그림과 같이 스도쿠 완성 조건을 만족하는 모든 column과의 교점에 1을 표기하면 된다.

만약 0이 들어가는 스도쿠 칸이 있다면, Exact Cover 형태를 만들기 위해 해당 칸에 들어갈 수 있는 모든 수에 대해서 위 표와 같은 형태로 1을 표기한다.
이를 통해 스도쿠 문제를 Exact Cover 문제로 치환할 수 있다.

Reference

profile
JaehyeokSong0
Hi there :D

0개의 댓글