빅오 표기법 (big-O notation) feat.Algorithm

- 빅오란 입력값이 무한대로 향할때 함수의 상한을 설명하는 수학적 표기 방법이다.

🔎 빅오는 점근적 실행 시간을 표기할때 가장 널리 쓰이는 수학적 표기 방법이다. 여기서 점근적 실행 시간이란 간단하게 n이라는 입력값이 무한대로 커질떄의 실행 시간의 추이를 의미한다.
따라서 충분히 큰 입력값에서의 알고리즘의 효율성에 따라 수행 시간이 크게 차이가 날 수 있다.

---

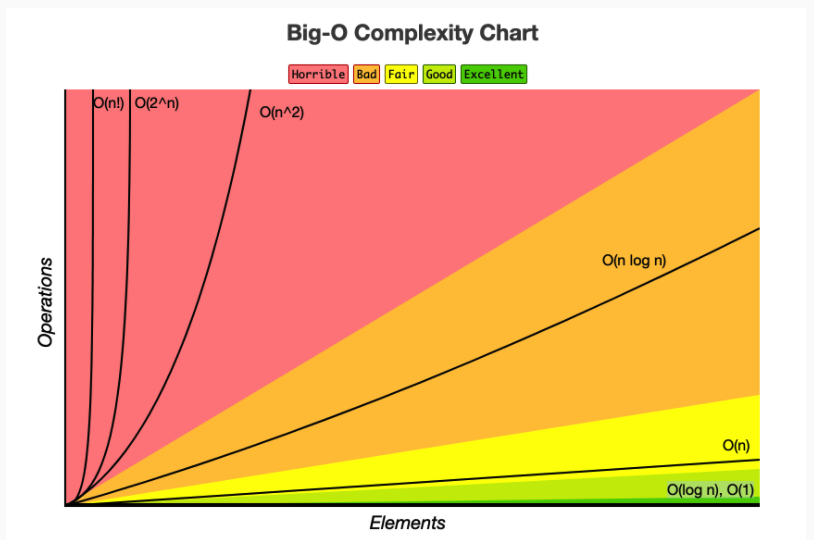
💡 빅오 표기법(big-O notation) 종류

O(1) - 스택에서 Push, Pop

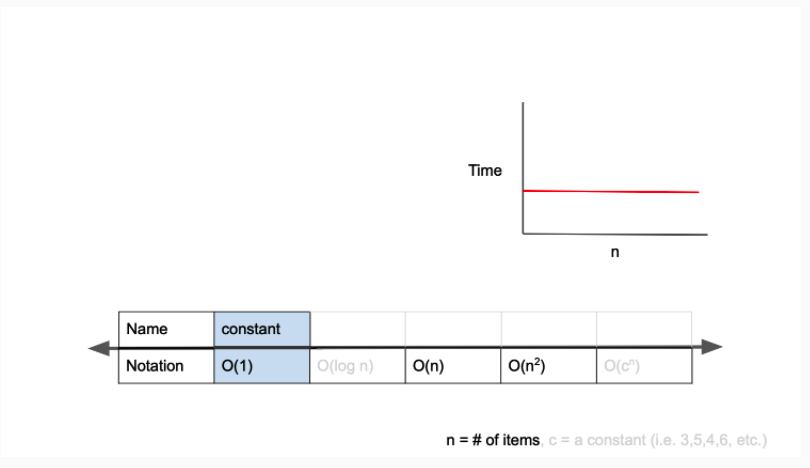
입력값에 상관없이 일정한 실행시간을 최고!의 알고리즘이라 할 수 있다. 하지만 상수 시간에 실행된다 해도 상수값이 상상 이상으로 클 경우 사실상 일정한 시간의 의미가 없다. 최고의 알고리즘이 될 수 있지만 그만큼 신중해야 한다.

• Big-O 표기법은 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?를 표기하는 방법
• O(1)는 constant complexity라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않습니다.
• 즉, 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다.

📌 코드 예시

function O_1_algorithm(arr, index) {
	return arr[index];
}

let arr = [1, 2, 3, 4, 5];
let index = 1;
let result = O_1_algorithm(arr, index);
console.log(result); // 2

O(n) - for 문

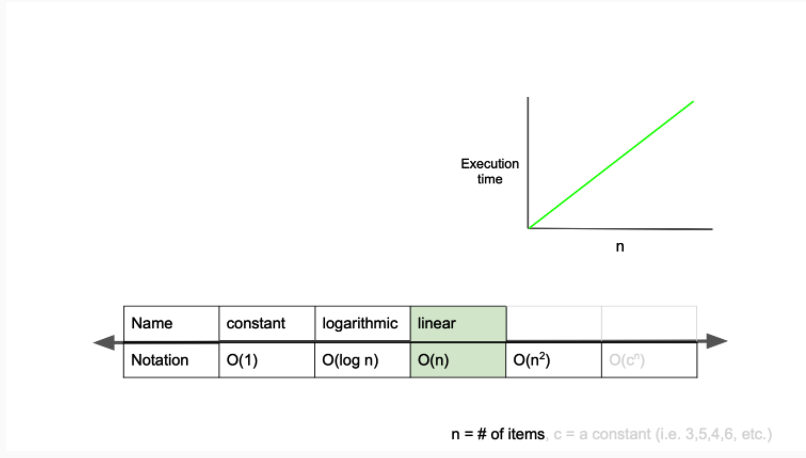
알고리즘을 수행하는데 걸리는 시간은 입력값에 비례한다. 이러한 알고리즘을 선형 시간 알고리즘이라 부른다. 정렬되지 않은리스트에서 최대 또는 최솟값을 찾는 경우가 해당되며 모든 입렵값을 적어도 한 번 이상은 살펴봐야 한다.

• O(n)은 linear complexity라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미합니다.
• 입력값이 1일 때 1초의 시간이 걸리고, 입력값을 100배로 증가시켰을 때 1초의 100배인 100초가 걸리는 알고리즘을 구현했다면, 그 알고리즘은 O(n)의 시간 복잡도를 가진다고 할 수 있습니다.

📌 코드 예시

function O_n_algorithm(n) {
	for (let i = 0; i < n; i++) {
	// do something for 1 second
	}
}

function another_O_n_algorithm(n) {
	for (let i = 0; i < 2n; i++) {
	// do something for 1 second
	}
}

O(log n) - 이진트리

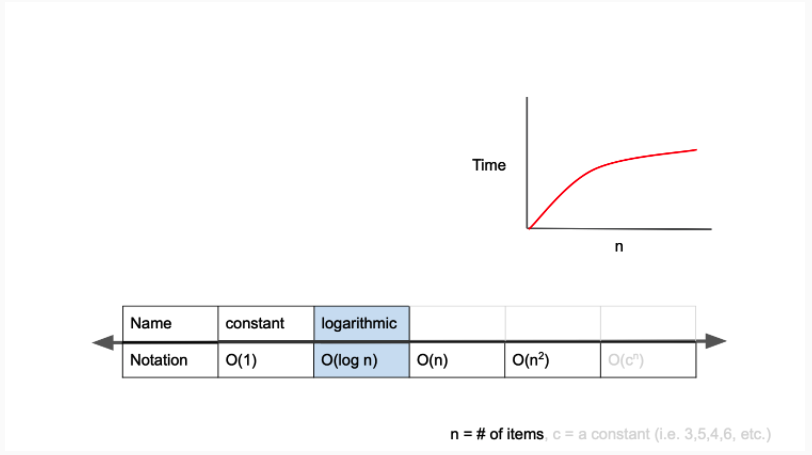
로그는 매우 큰 입력값에서도 크게 영향을 받지 않는 편이다. 매우 견고한 알고리즘으로 이진 탐색의 경우가 이에 해당한다.

• O(log n)은 logarithmic complexity라고 부르며 Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가집니다.
• 자료구조에서 배웠던 BST(Binary Search Tree)의 경우 BST에선 원하는 값을 탐색할 때, 노드를 이동할 때마다 경우의 수가 절반으로 줄어듭니다.

이해하기 쉬운 게임으로 비유해 보자면 up & down을 예로 들 수 있습니다.

1. 1~100 중 하나의 숫자를 플레이어1이 고른다 (30을 골랐다고 가정합니다).
2. 50(가운데) 숫자를 제시하면 50보다 작으므로 down을 외친다.
3. 1~50중의 하나의 숫자이므로 또다시 경우의 수를 절반으로 줄이기 위해 25를 제시한다.
4. 25보다 크므로 up을 외친다.
5. 경우의 수를 계속 절반으로 줄여나가며 정답을 찾는다.
6. 매번 숫자를 제시할 때마다 경우의 수가 절반이 줄어들기 때문에 최악의 경우에도 7번이면 원하는 숫자를 찾아낼 수 있게 됩니다.
7. BST의 값 탐색도 같은 로직으로 O(log n)의 시간 복잡도를 가진 알고리즘(탐색기법)입니다.

O(n2) - 이중 for 문, 삽입정렬(insertion sort), 거품정렬(bubble sort), 선택정렬(selection sort)

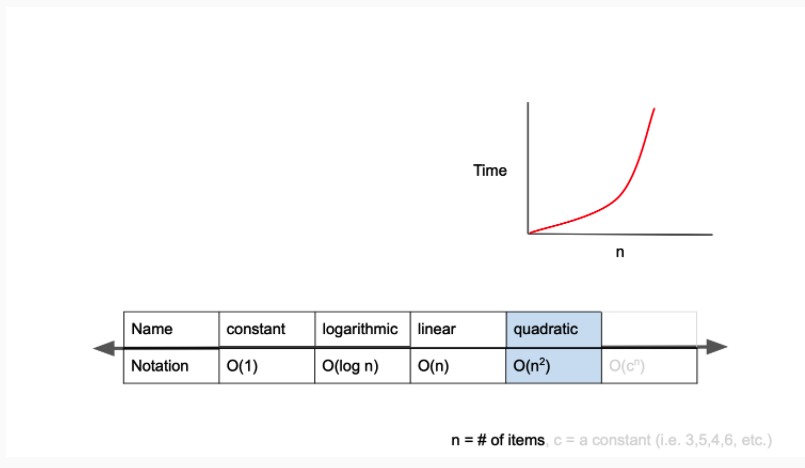
버블 정렬 같은 비효율저긴 정렬 알고리즘이 이에 해당 한다.

• O(n2)은 quadratic complexity라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미합니다.

• 예를 들어 입력값이 1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 된다면, 이 알고리즘의 시간 복잡도는 O(n2)라고 표현합니다.

📌 코드 예시

function O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
		// do something for 1 second
		}
	}
}

function another_O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
			for (let k = 0; k < n; k++) {
			// do something for 1 second
			}
		}
	}
}

O(2n) - 피보나치 수열(재귀)

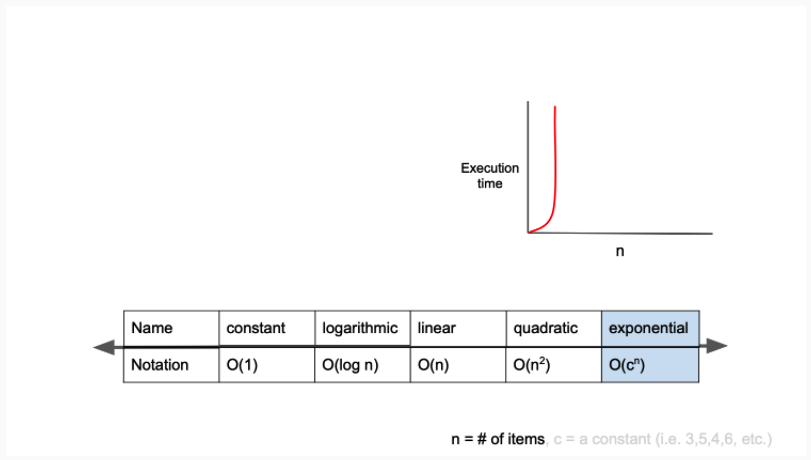
• O(2n)은 exponential complexity라고 부르며 Big-O 표기법 중 가장 느린 시간 복잡도를 가집니다.
• 종이를 42번 접으면 그 두께가 지구에서 달까지의 거리보다 커진다는 이야기를 들어보신 적 있으신가요?
  고작 42번 만에 얇은 종이가 그만한 두께를 가질 수 있는 것은, 매번 접힐 때마다 두께가 2배로 늘어나기 때문입니다.

📌 코드 예시

function fibonacci(n) {
	if (n <= 1) {
		return 1;
	}
	return fibonacci(n - 1) + fibonacci(n - 2);
}