피보나치 수열 효율적으로 구현하기(Dynamic programming)

• 피보나치 수열: n번째 수는 n-1번째와 n-2번째 수를 합하여 수열
  ex)0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

👉 기존 피보나치 수열을 구하는 방식 ( 6번째 수 라고 가정)

function fibonacci(n) {
  // TODO: 여기에 코드를 작성합니다.

  if(n<=1){
	return n;
  }
 return fibonacci(n-1)+fibonacci(n-2)
}

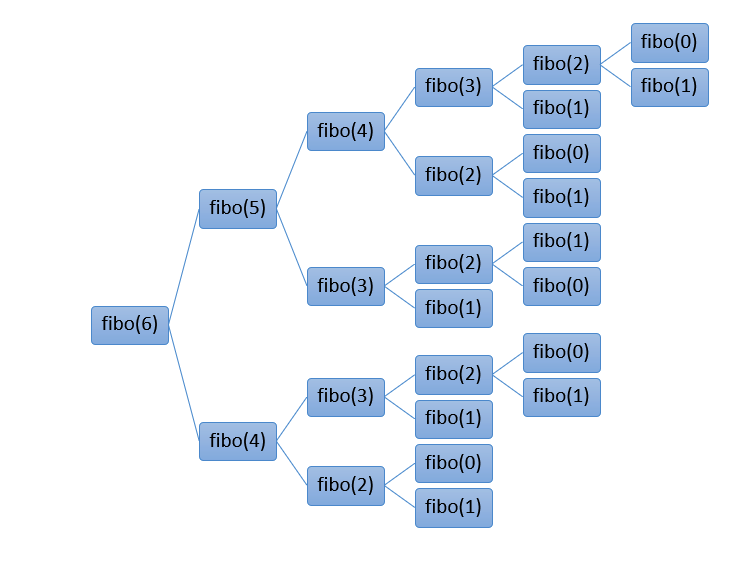
✓ n의 수가 커질수록 함수를 중복적으로 호출 하는 횟수가 점점 커지고 런타임이 매우 길어짐
✓ 이렇게 함수를 수행하는데 걸리는 시간이 증가하는 것을 #시간복잡도가 가파르게 상승

👉 동적 계획법 (Dynamic programming)으로 구현하기

1. 문제를 부분 문제로 나눈다.
2. 가장 작은 문제를 해를 구한 뒤, 테이블에 저장한다.
3. 테이블에 저장되어있는 데이터로 전체의 문제의 해를 구한다.

let fibonacci = function (n) {
    console.log("function start")
    console.time("fibonacci Function")
    const memo = [0, 1];
    const aux = (n) => {
      // 이미 해결한 적이 있으면, 메모해둔 정답을 리턴한다.
      if (memo[n] !== undefined) return memo[n];
      // 새롭게 풀어야하는 경우, 문제를 풀고 메모해둔다.
      memo[n] = aux(n - 1) + aux(n - 2);
      return memo[n];
    };
    console.timeEnd("fibonacci Function")
    return aux(n);
  };

이와 같은 방식으로 접근하여 풀 수 있다.

👉 위 두가지 방식에 console.time과 console.timeEnd를 통해 실제 연산까지 걸리는 런타임을 측정한 결과 약 두 배 정도 속도 차이가 나는 것을 확인할 수 있었다.