최적화 문제를 위한 알고리즘.
동적 프로그래밍과 유사하지만
동적 프로그래밍보다 더 간단하고 효율적인 해가 존재하는 문제에 사용하는 알고리즘
항상 각 단계에 있어서 가장 좋을 것이라 생각되는 선택이
전체적으로 최적해로 안내될 것이라는 바램으로
부분적으로 최적인 선택을 하는 알고리즘이다.
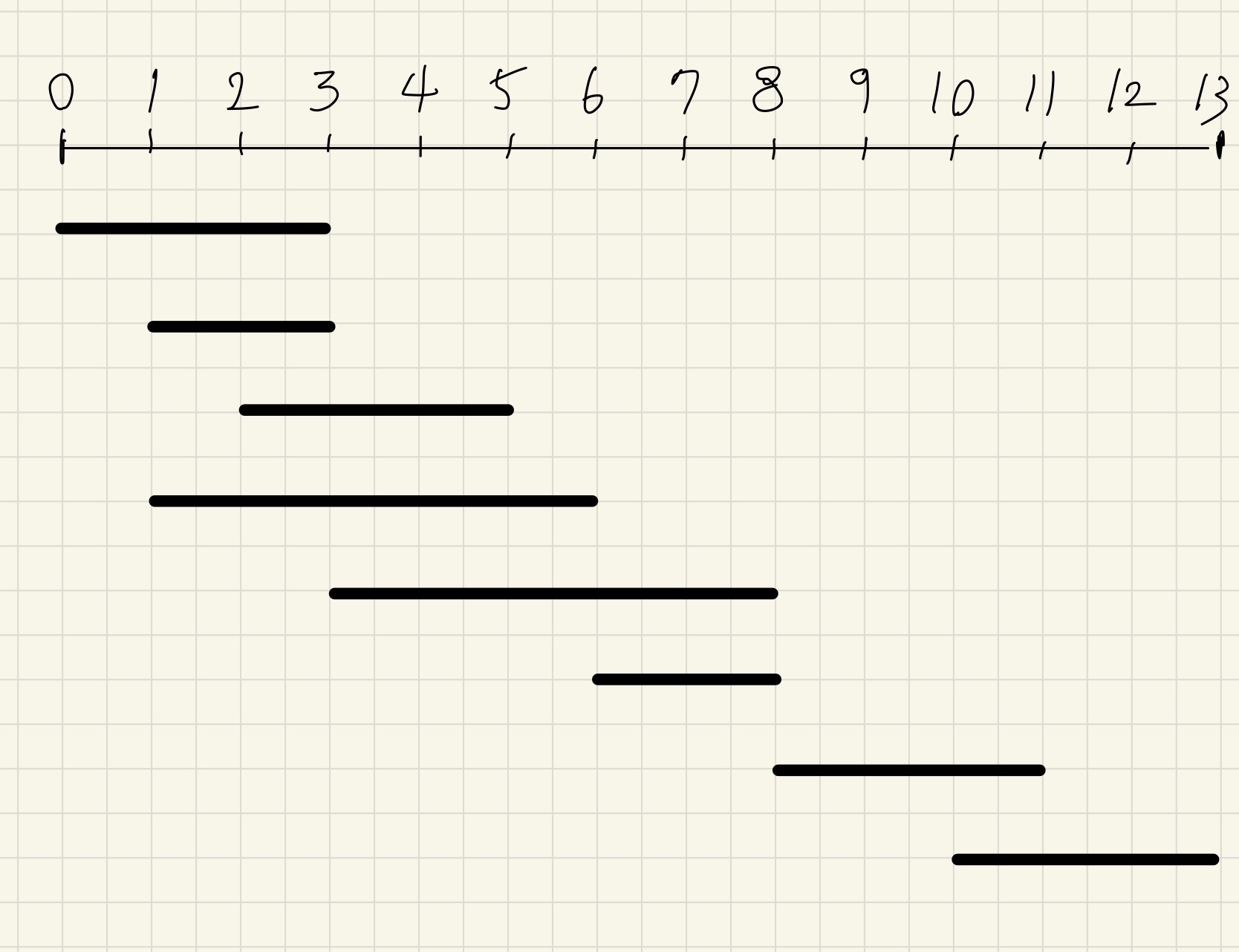
활동 선택 문제
n개의 활동이 공유 자원을 배타적으로 사용해야 할 때
겹치지 않는 활동들(nonoverlapping activities)을 포함하는
가장 큰 가능한 활동 집합을 선택하는 문제.
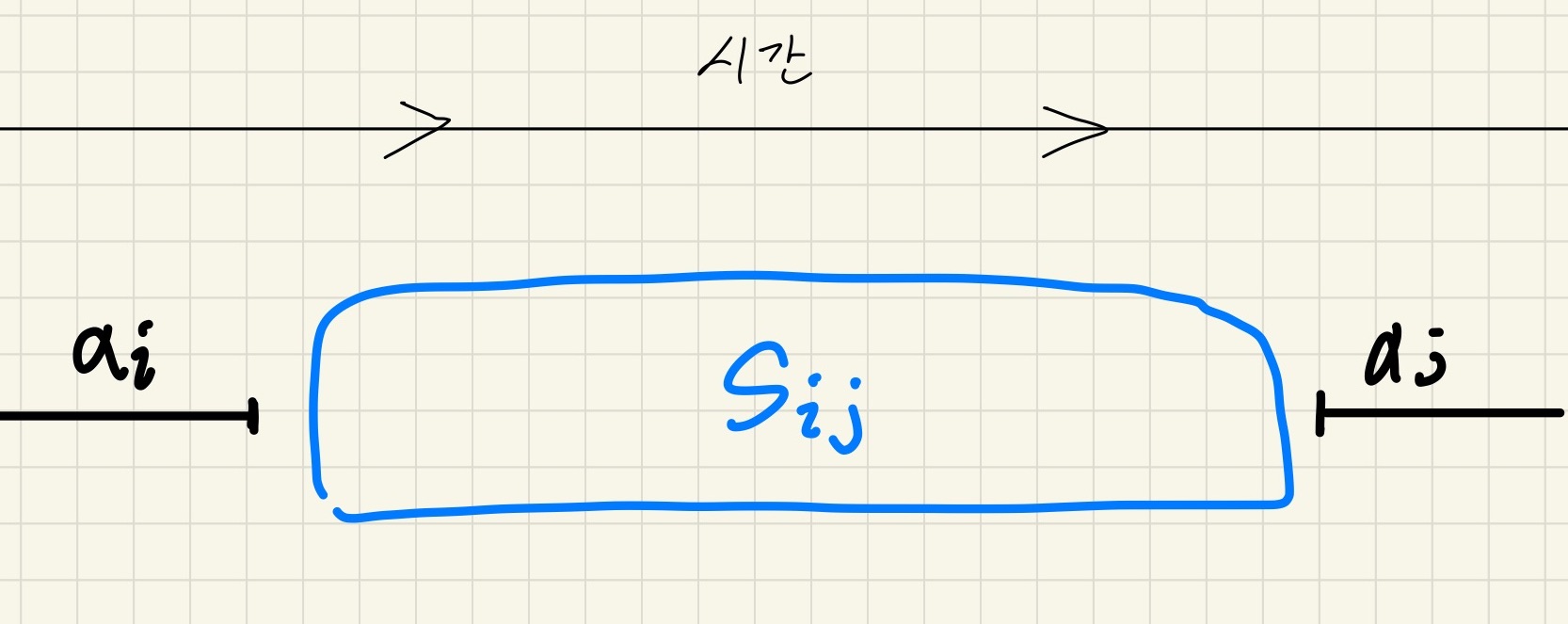
각 활동는 시작시간()과 종료시간()이 있고,
이들은 을 만족한다.
어려운 말을 쓴다.
BOJ 1931 회의실 배정 문제로
바꿔서 표현해보자.
n개의 회의가 한 개의 강의실에 신청되어 있을 때,
최대한 많은 회의를 할 수 있도록 스케줄을 짜는 문제.
편안하다.
📍공유 자원 : 한 개의 강의실
📍n개의 활동 : 신청된 n개의 회의
📍배타적 사용 : 한 강의실에서 여러개의 회의가 동시에 진행될 수 없음
📍가장 큰 가능한 활동 집합 : 최대한 많은 회의를 할 수 있는 스케줄
그리디 선택
✅ 최적 부분 구조(Optimal Substructure)를 갖는지
1.
회의 가 종료한 후에 시작하고, 회의 가 시작하기 전에 종료하는 회의들의 집합을 라고 하자.
에 들어있는, 겹치지 않게 스케줄을 짤 때 최대로 회의를 넣은 집합(스케줄)이
어떤 회의 를 포함하는 라고 가정 하자.
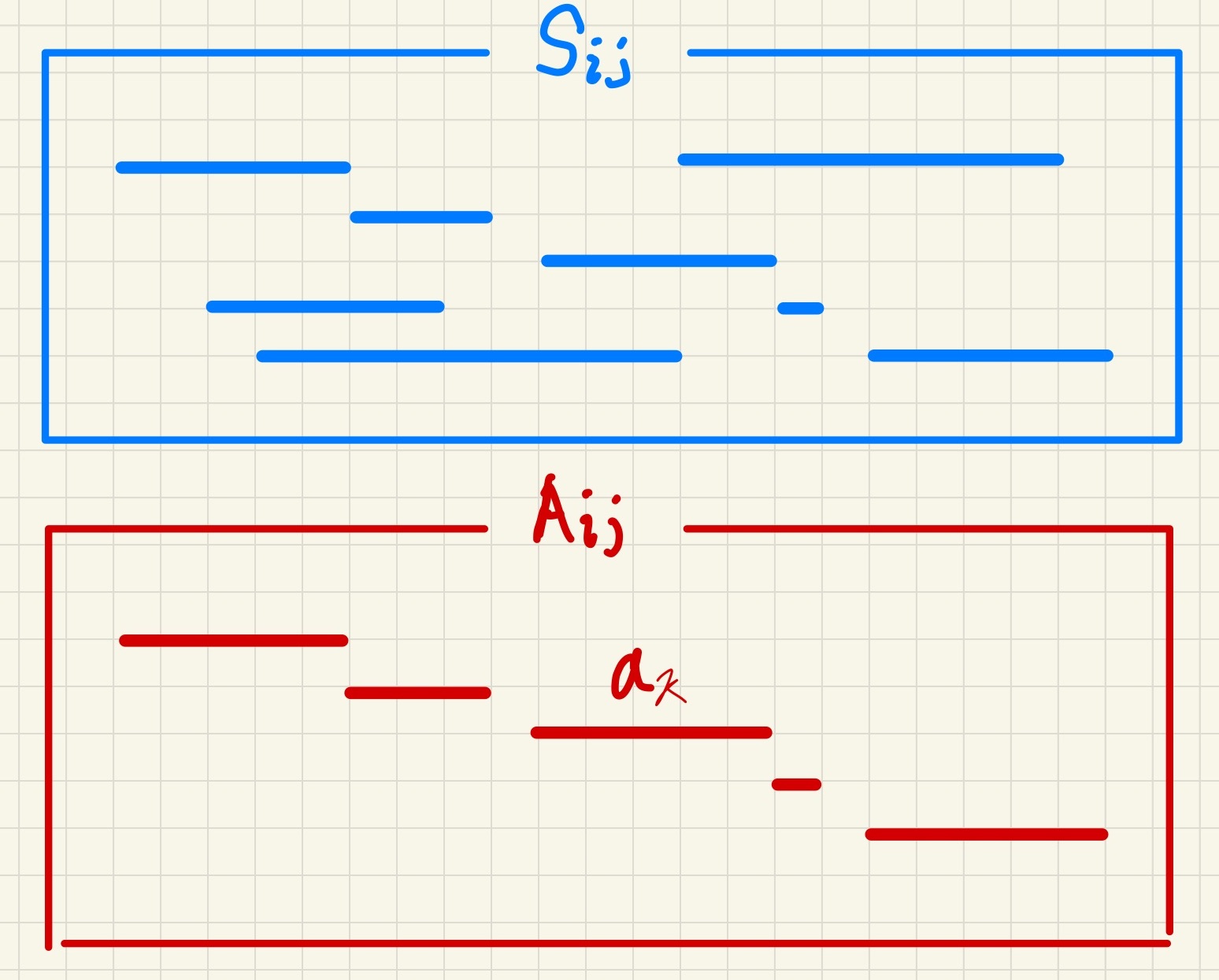
최적해에 를 포함하면
와 에서
각각 겹치지 않게 스케줄을 짤 때, 최대로 회의를 넣은 집합(스케줄)을 찾는
2개의 부분 문제로 나눠진다.
는 회의가 시작되기 전에 종료되는 회의를 포함하고,
는 회의가 끝난 이후에 시작되는 회의를 포함한다.
따라서,
는 개의 회의로 이루어진다.
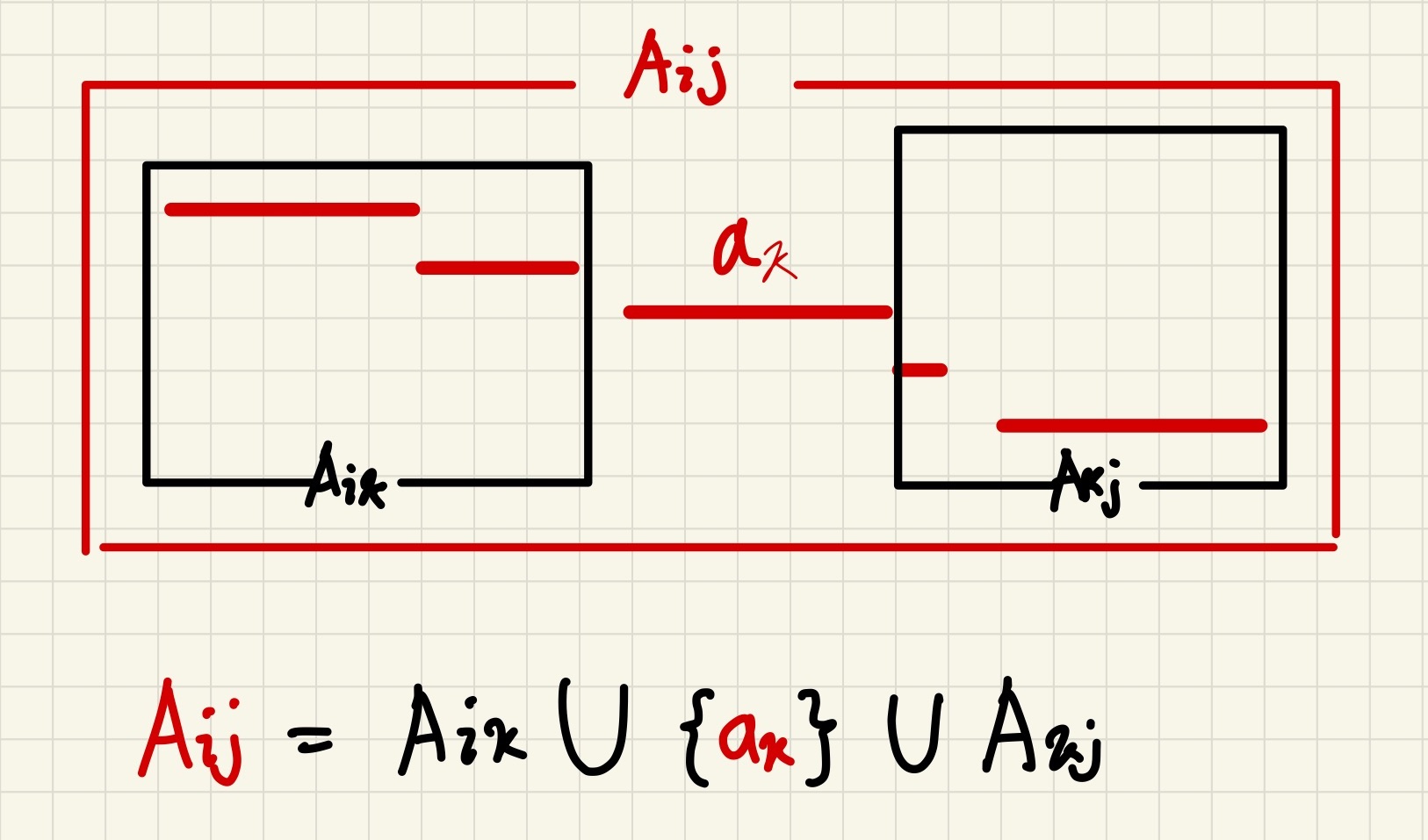
2.
최적해 는 두 부분문제 와 에 대한 최적해를 포함해야 한다.
만약 를 만족하는 를 찾을 수 있다면,
개의 회의를 가지는 집합(스케줄)을 만들게 되는데,
이는 가 최적해 라는 가정에 모순이다.
따라서 활동 문제는 전체 최적해가 부분 문제의 최적해를 포함하는,
최적 부분 구조를 가진다.
✅ 그리디 선택
가능한 최대로 많은 회의를 할 수 있도록 하는 회의를 선택해야한다.
에 들어있는 회의 중 가장 빠른 종료시간을 갖는 회의를 선택해야
그 회의 뒤에 시작하는 회의의 수가 가장 최대가 되도록 해줄 수 있기 때문에,
최종 최적해에 들어있는 회의 중 하나는 반드시 맨 먼저 종료되는 회의이어야 한다.
1.
회의들이 종료 시간에 대해 오름차순으로 정렬되어있다고 한다면,
그리디 선택은 맨 처음으로 끝나는 회의인 을 선택하는 것이다.
을 선택하면,
종료 후에 시작하는 회의들만을 가지고 겹치지 않는 회의를 찾는 부분 문제만 남는다.
(이고, 는 어떤 회의들 중에서도 가장 빠른 종료 시간이므로 어떤 회의도 보다 작거나 같은 종료 시간을 가질 수 없음)
따라서 와 겹치지 않는 회의들은 종료 이후에 시작해야한다.
또한 활동 선택 문제는 최적 부분 구조를 가지는 문제임을 증명했으므로,
회의 이후에 오는 회의들의 집합을 라고 할 때,
를 선택한 뒤에는 이 풀어야 할 유일한 부분문제로 남는다.
최적해에 회의 가 포함되어있다면,
원래 문제에 대한 최적해는
회의 와 부분 문제 에 대한 최적해로 구성된다.
2. 그리디 선택이 언제나 최적해에 포함되는지
부분 문제에서 가장 종료 시간이 빠른 회의를 이라고 하고
에서 종료 시간이 가장 빠른 회의를 라고 하자,
1)
이 에 들어있는 '겹치지 않는 회의들로 구성된 최대 크기의 어떤 부분 집합(스케줄)'에 들어있음
= 부분 문제의 최적해에 포함됨
-> 증명 끝
2)
의 를 으로 바꿔준 집합을 라고 하자,
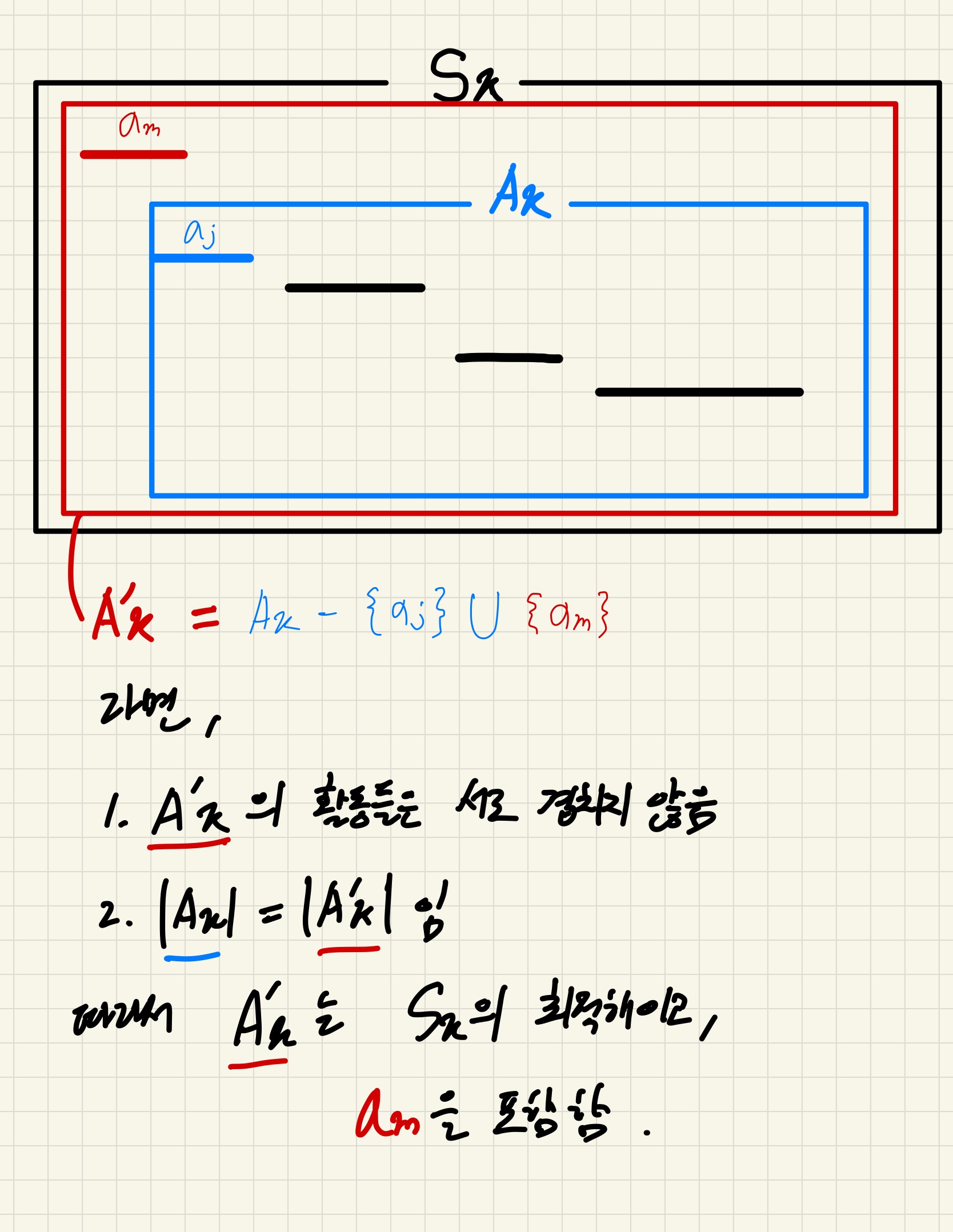
그림에서 설명한 것 처럼
의 회의들은 서로 겹치지 않고
가 에서 가장 빨리 끝나는 회의이므로 이며
이다.
따라서 는 의 서로 겹치지 않는 회의들의 최대 크기 부분 집합 이므로
의 부분 문제의 최적해이고,
의 부분 문제의 최적해가 에서 가장 종료시간이 빠른 회의 을 포함하고 있다.
따라서 그리디 선택은 언제나 최적해에 들어있다.
BOJ 1931 회의실 배정
위 증명에서 알 수 있듯,
주어진 활동(회의)을 종료 시간을 기준으로 오름차순 정렬 후에
처음에는 가장 종료 시간이 빠른 회의를 스케줄에 넣어주고
이후 부터는 최근에 넣은 희의의 종료시간 이후에 시작하는 회의를
스케줄에 넣어주면 된다.
다만 이 문제에서는
끝 시간이 같다면 시작 시간을 기준으로 오름차순 정렬해주어야 하는데
시작 시간을 정렬해주는 이유는
"회의의 시작시간과 끝나는 시간이 같을 수도 있다." 라는 조건 때문이다.
아래 처럼 시작과 동시에 끝나는 회의가 있으면서
시작 지점을 기준으로 한 정렬이 이루어지지 않은 경우 반례가 발생한다.
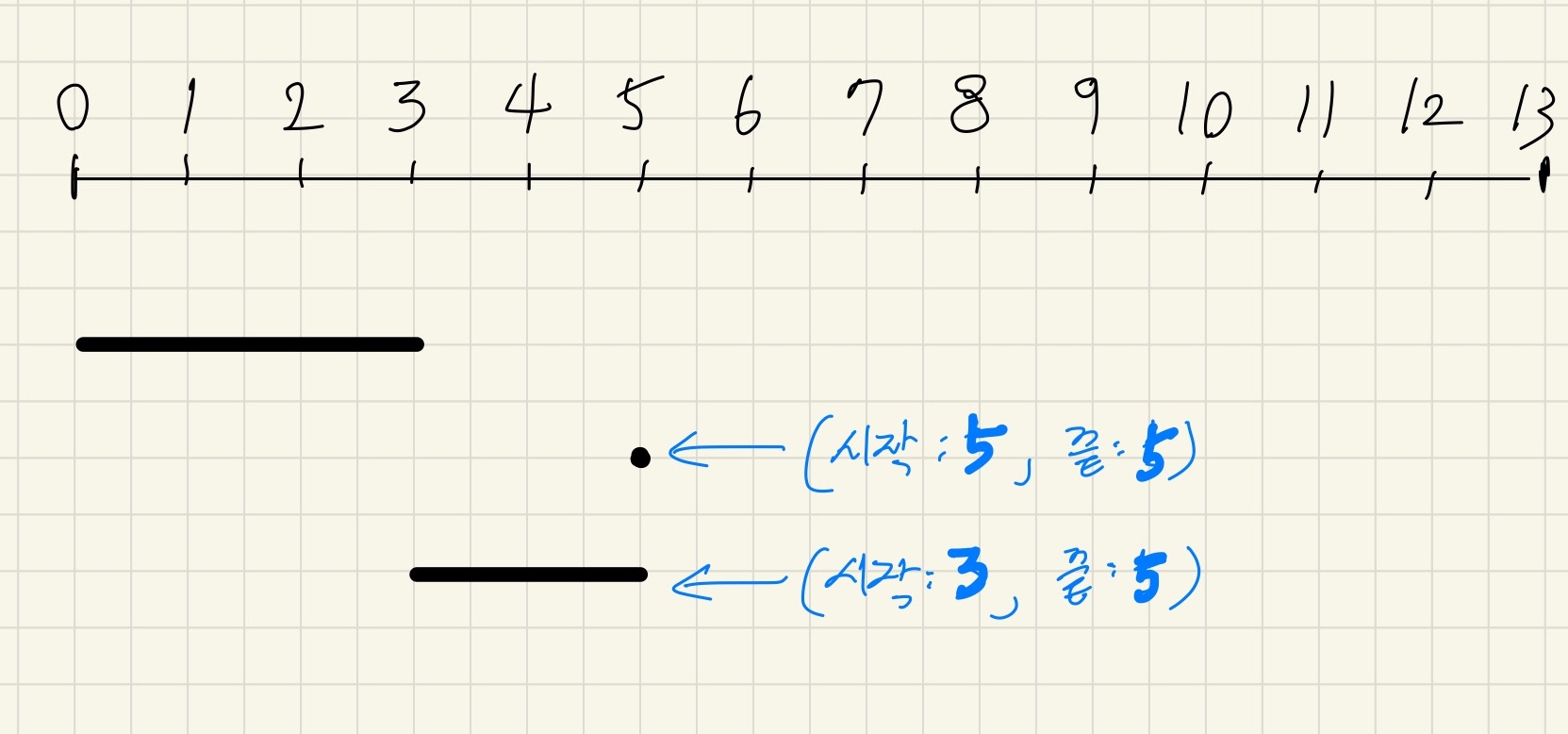
회의를 (시작, 끝)으로 표현할 때,
첫번째 회의인 (0, 3) 는 스케줄에 담을 수 있다.
두번째 회의인 (5, 5) 또한 스케줄에 담을 수 있다.
세번째 회의인 (3, 5) 는 스케줄에 담지 못한다.
( 이 전까지 스케줄에 저장된 마지막 회의가 5시에 끝나는데, 세번째 회의는 3시에 시작하기 때문이다. )
끝 시간이 같을 때 시작 시간으로 오름차순 정렬을 해 줄 경우,
위와 같은 상황을 방지할 수 있다.
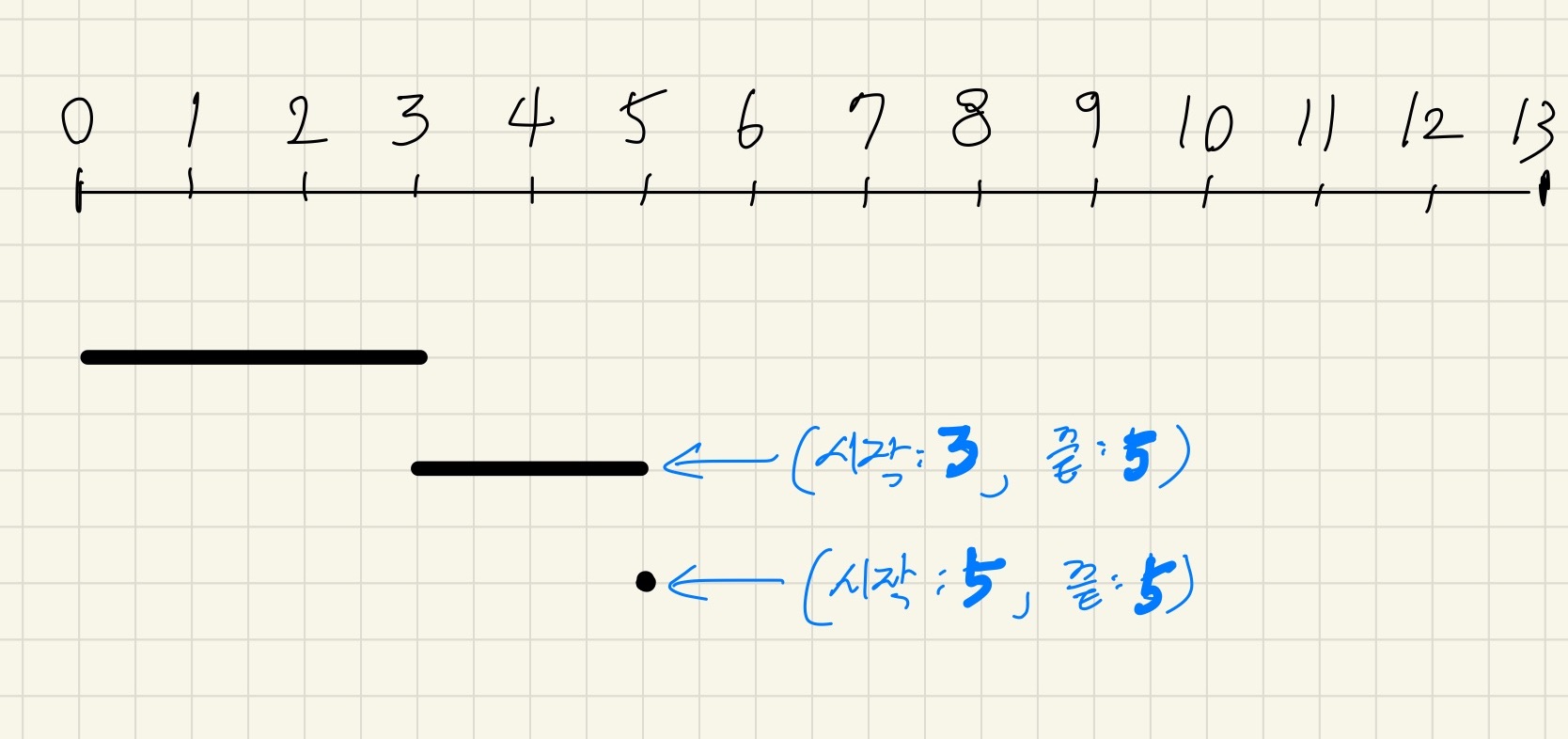
첫번째 회의인 (0, 3) 는 스케줄에 담을 수 있다.
두번째 회의인 (3, 5) 또한 스케줄에 담을 수 있다.
세번째 회의인 (5, 5) 또한 스케줄에 담을 수 있다.
[ 전체 코드 ]
import sys
n = int(sys.stdin.readline().rstrip())
# 끝시간을 기준으로 오름차순 정렬, 끝시간이 같으면 시작 시간으로 오름차순 정렬
time = sorted([tuple(map(int, sys.stdin.readline().split())) for _ in range(n)], key= lambda x: (x[1], x[0]))
end = 0
count = 0
for s, e in time:
if end <= s:
end = e
count += 1
sys.stdout.write(f'{count}')
엠씨그리디