BOJ 1074: Z

문제 : BOJ 1074 Z

크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색한다.

아래는 순서대로 각각 N = 1, N = 2, N = 3 일 때의 예시이다.

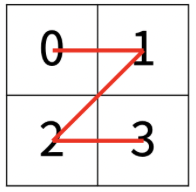
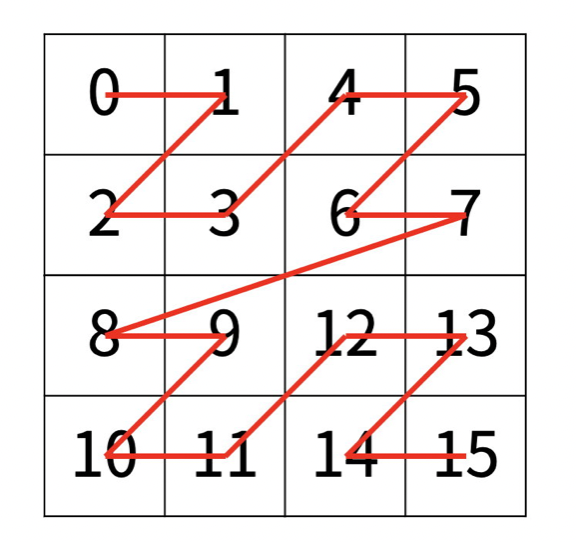
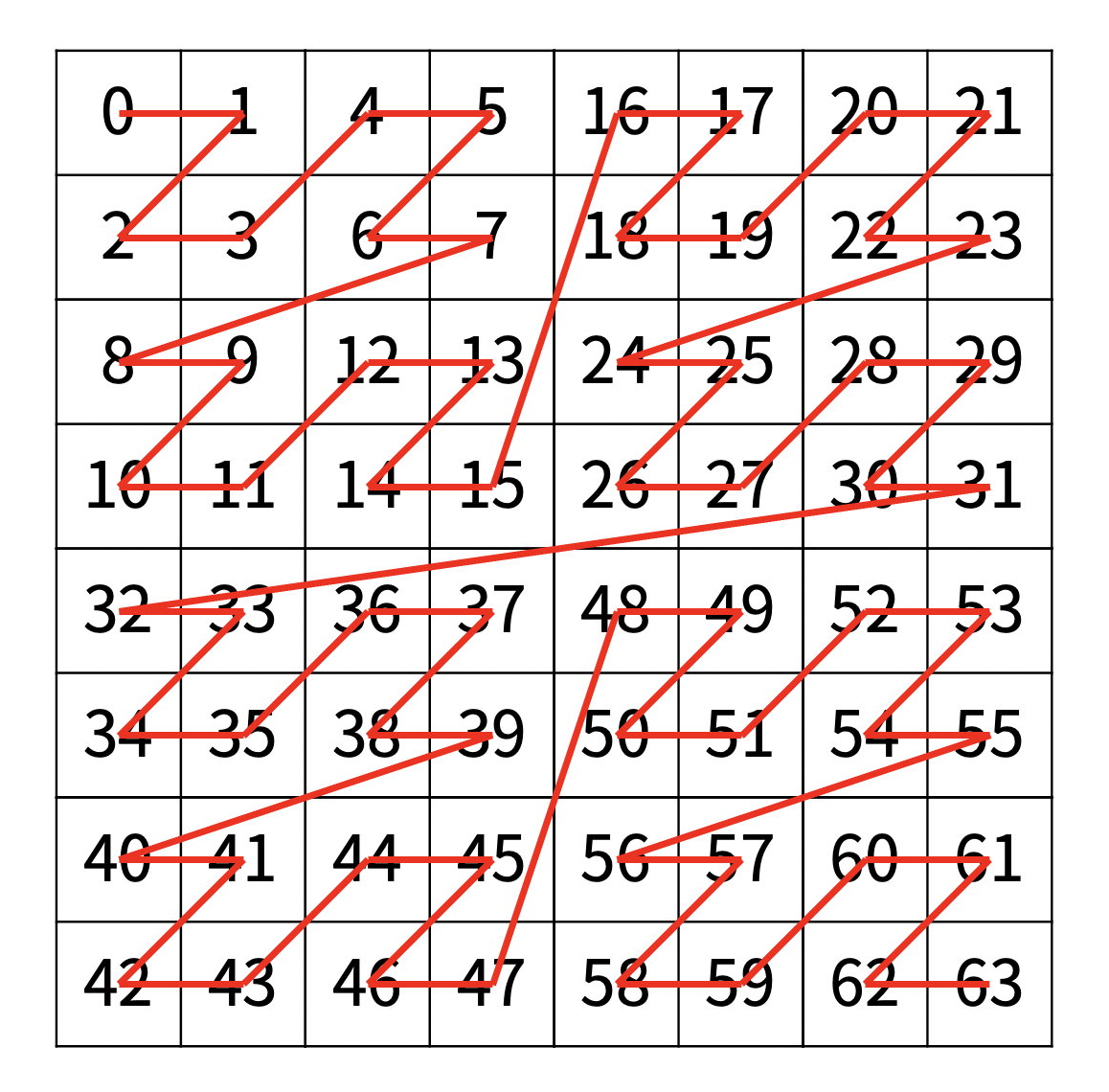
💡아이디어

2차원 배열을 4개로 분할하자

문제에서 다음과 같은 조건이 주어진다.

N > 1 일 때
$2^N \times 2^N$배열을 방문 할 때
$2^{N-1} \times 2^{N-1}$ 배열로 4등분 하여 Z 모양으로 방문한다.

4개로 분할된 4개의 2차원 배열을
Z모양 순서대로 1번, 2번, 3번, 4번 배열이라고 하자.

이 때, 분할된 각 배열 내 행과 열의 방문 순서는 연속적이므로,
각 부분 배열에 존재할 수 있는 행과 열의 방문 순서는 범위로 표현 할 수 있다.

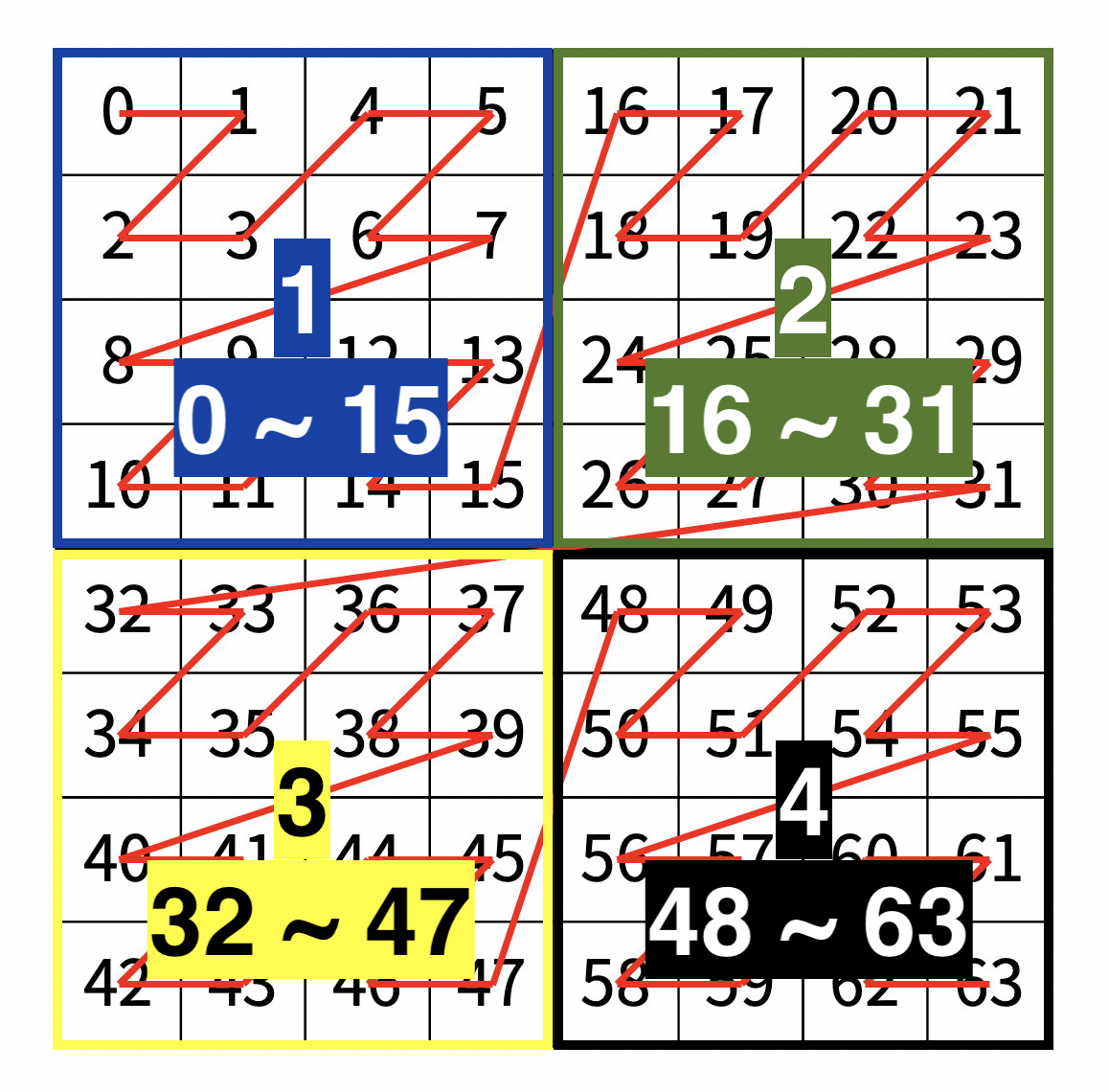
규칙을 찾자

전체 배열의 크기를 $2^N \times 2^N$, 해당 배열의 최소 방문 순서를 m 이라고 할 때,
각 부분 배열이 가질 수 있는 방문 순서의 범위는 아래와 같다.

• 1번 배열 :
  m
  ~ m + $(2^{N-1} \times 2^{N-1}) -1$
• 2번 배열 :
  m + $(2^{N-1} \times 2^{N-1})$
  ~ m + $(2^{N-1} \times 2^{N}) - 1$
• 3번 배열 :
  m + $(2^{N-1} \times 2^{N})$
  ~ m + $(2^{N-1} \times 2^{N-1}) + (2^{N-1} \times 2^{N}) - 1$
• 4번 배열 :
  m + $(2^{N-1} \times 2^{N-1}) + (2^{N-1} \times 2^{N})$
  ~ m + $(2^{N} \times 2^{N})-1$

🧑‍💻구현 해보자

위에서 찾은 규칙을 보면
한번의 분할이 일어날 때 마다
4개의 배열에 존재할 수 있는 방문 순서의 최소값은 각각 다르다.

따라서, 배열을 점점 분할하며
최종 방문 순서를 알아내는데 필요한 값은
입력받은 N, r, c 그리고
각 재귀 호출마다 바뀌는 해당 분할 배열에 존재할 수 있는 방문 순서의 최소값이다.

배열을 더 이상 분할 할 수 없을때까지 분할(재귀 호출)을 반복하면,
마지막에 전달된 최소값은 곧 (r,c)의 방문 순서이다.

[ 전체 코드 ]

N, r, c = map(int, input().split())

def get_num(min, N, r, c):
    if N == 0:
        print(min)
        return

    if r < 2 ** (N-1):
        if c < 2 ** (N-1):
            get_num(min, N-1, r, c)
        else:
            c -= 2 ** (N-1)
            get_num(min + (2 ** (N-1)) ** 2, N-1, r, c)
    else:
        r -= 2 ** (N-1)
        if c < 2 ** (N-1):
            get_num(min + (2 ** (N-1)) * (2 ** (N)), N-1, r, c)
        else:
            c -= 2 ** (N-1)
            get_num(min + (2 ** (N-1)) ** 2 + (2 ** (N-1)) * (2 ** (N)), N-1, r, c)
    

get_num(0, N, r, c)

---