BOJ 8983 사냥꾼

문제 : BOJ 8983 사냥꾼

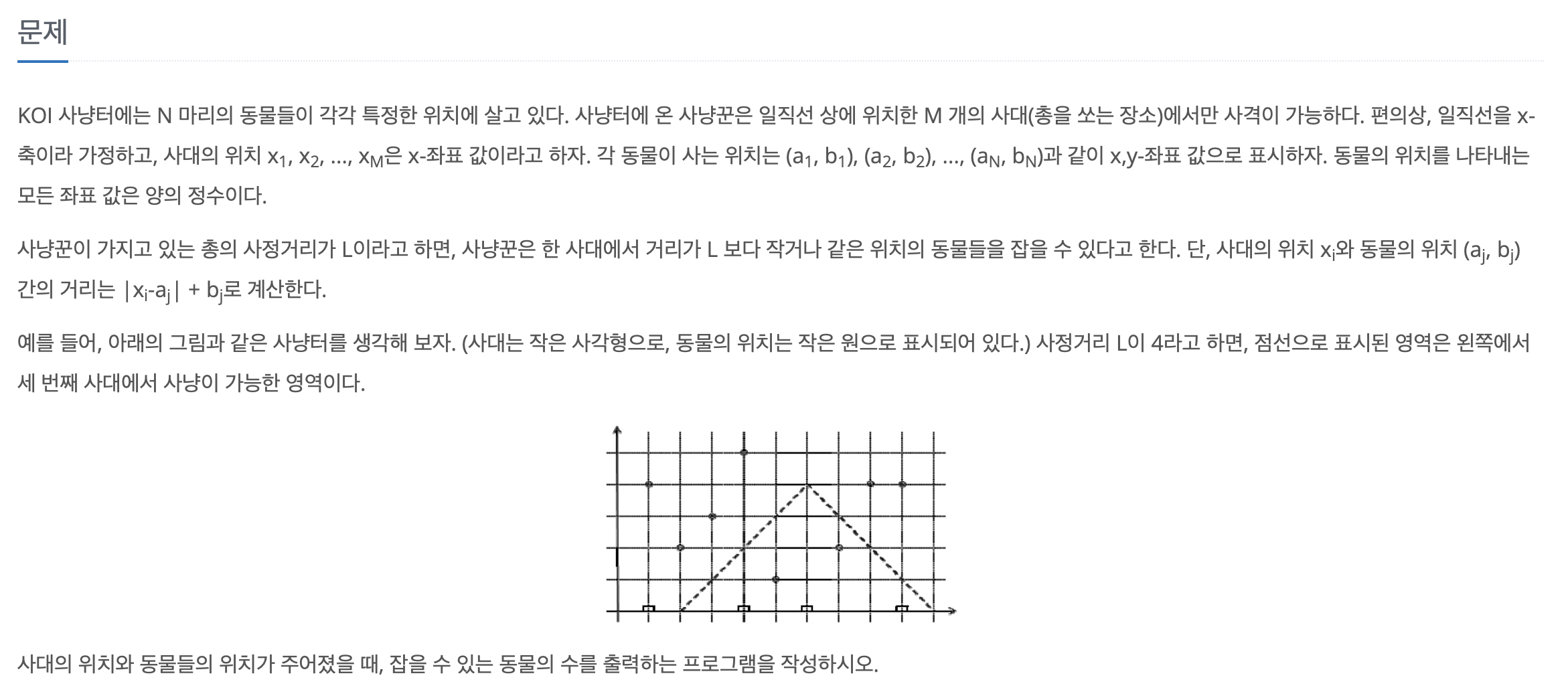
사대와 동물들의 좌표, 총의 사정거리가 주어진다.
사대는 일직선 상에 위치하고, 동물들의 좌표는 (x, y) 좌표값으로 주어진다.
또, 사대와 동물간의 거리를 구하는 공식도 따로 주어지고
이때 잡을 수 있는 동물의 수를 구해야 한다.

접근

발상의 전환이 필요한 이분탐색 문제이다.

각 사대에서 동물을 바라보며 잡을 수 있는 동물의 수를 센다면
사정거리 내에 존재할 수 있는 동물들을 모두 탐색해 주어야 한다.

하지만 동물의 입장에서 사대를 바라본다고 생각하면,
'나(동물)와 가장 가까운 사대의 사정거리에 내가 들어가는지' 만을 판단해주면 된다.

구현

문제의 조건에 따라
y좌표값이 사정거리의 길이보다 큰 좌표에 위치하는 동물들은 사냥할 수 없다.
따라서 탐색 기준에서 제외시켜 주었다.

구현할 때 생각이 많았던 부분은, 양 끝점을 축소시키기 위한 판단 기준을 어떻게 잡느냐였다.

입력 받은 각 동물들의 좌표를 하나씩 순회하며 이분 탐색을 반복한다고 할 때
현재 탐색중인 사대와 동물의 거리는
1) 사정거리보다 크거나
2) 사정거리보다 작거나 같을 것이다.

1) 사정거리보다 작거나 같은 경우

안타깝게도 해당 동물은 사냥당했다. 더 이상 탐색을 진행해주지 않아도 된다.

2) 사정거리보다 큰 경우

약간 모호할 수 있는데,
동물과 사대의 거리가 사정거리보다 큰 경우는
1-1) 동물이 사대의 왼쪽에 있으면서 사정거리 바깥에 위치하거나
1-2) 동물이 사대의 오른쪽에 있으면서 사정거리 바깥에 위치하거나
두가지 경우가 존재한다.

따라서, 현재 탐색중인 사대의 x좌표와 동물의 x좌표를 비교하여
사대의 x좌표 > 동물의 x좌표 인 경우 끝점을 중간지점으로 줄여주고,
반대로 사대의 x좌표 < 동물의 x좌표 인 경우 시작점을 중간지점으로 키워준다.

사대와 동물의 거리가 사정거리보다 크면서
사대의 x좌표 == 동물의 x좌표 인 경우는 존재하지 않는데,
이미 탐색 대상에서 y좌표값이 사정거리보다 큰 동물은 사냥할 수 없기 때문에
탐색의 기준으로 사용하지 않았기 때문이다.

이분 탐색을 진행하며
각 경우에서 동물이 가장 가까운 사대의 사정거리 안에 들어온 순간
사냥이 가능하다고 판단하고,
모든 순회가 종료된 뒤에도 사정거리에 들지 못했다면
사냥이 불가능하다고 할 수 있다.

[ 전체 코드 ]

import sys

m, n, l = map(int, sys.stdin.readline().split())

spot = sorted(list(map(int, sys.stdin.readline().split())))

count = 0
def solution(animal, l):
    # global count
    s = 0
    e = len(spot)-1
    while s < e:
        m = (s+e) // 2
        # spot[m]과 동물의 거리가 l보다 클경우
        if abs(spot[m]-animal[0]) + animal[1] > l:
            # 사대의 x좌표가 동물의 x좌표보다 클 경우
            if spot[m] > animal[0]:
                e = m - 1
            # 사대의 x좌표가 동물의 x좌표보다 작을 경우
            # :: 같을 경우는 존재하지 않음 
            # (입력 단계에서 y>l인 경우를 받지 않았기 때문에, 동물과 사대 사이의 거리가 l보다 크면서 x좌표는 같을 경우는 존재하지 않는다.)
            else:
                s = m + 1
        # spot[m]과 동물의 거리가 l보다 작거나 같을경우
        else:
            # 사냥 가능하므로 count를 1 증가시키고 종료
            # count += 1
            return 1
    if abs(spot[e]-animal[0]) + animal[1] <= l:
        # count += 1
        return 1
    else:
        return 0

# 동물 좌표를 입력 받는대로 탐색
for _ in range(n):
    tmp = list(map(int, sys.stdin.readline().split()))
    # y좌표가 l보다 작거나 같을때만 탐색 진행
    if tmp[1] <= l:
        count += solution(tmp, l)


sys.stdout.write(f'{count}')

---