삽입(insert)

insert 자체는 BST와 동일하게 진행되고,
insert 이후 RB트리를 유지시키기 위한 fix up이 진행된다.

먼저 insert부터 확인해보자.

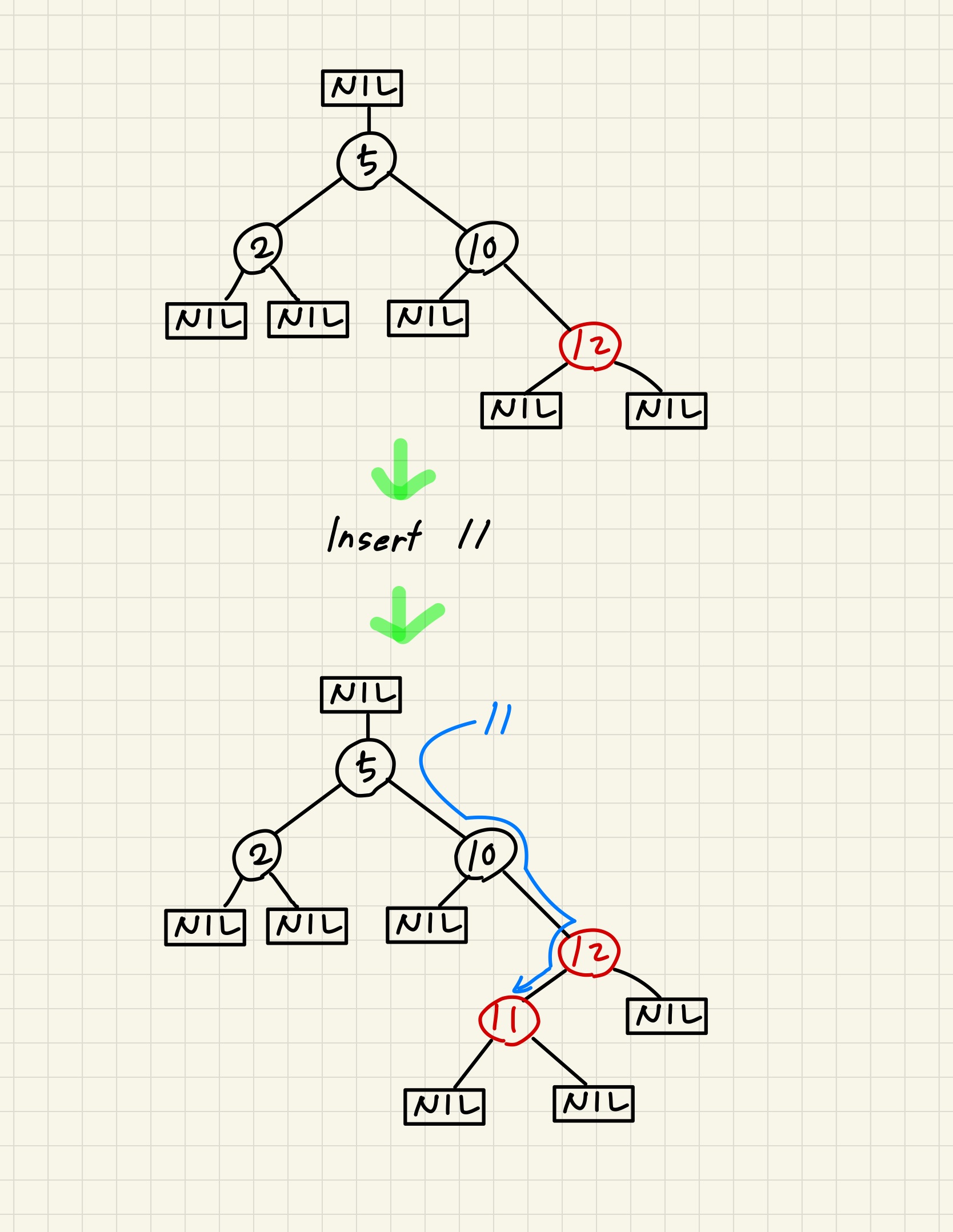
Root node부터 시작해서,
현재 insert하려는 new_node의 key값과 만나는 node의 key값을 비교한 뒤
new_node의 key값이 더 작다면 왼쪽으로, 크다면 오른쪽으로 내려간다.
더 이상 내려갈 수 없을 때(nil을 만날 때) 그 위치가 new_node가 삽입 될 위치이다.

다만,

RB 트리의 1번 조건에 따라, 모든 node는 RED 또는 BLACK의 색을 가져야 하는데,
새로 insert되는 node의 색은 항상 RED 로 고정된다.

이는 RB Tree의 조건 5번을 위배하지 않기 위함이다.

5. 각 노드로부터 그 노드의 자손인 리프로 가는 경로들은 모두 같은 수의 BLACK 노드를 포함해야함

만약 추가되는 node의 색이 BLACK 이라면,
어떤 node에서 출발해서 leaf로 갈 때,
추가된 node로 가는 경로의 BLACK 노드 개수가 다른 경로보다 1개 더 많아질 것이고,
이는 조건 5번을 위배한다.

따라서 Insert되는 node의 색은 RED 로 고정된다.

💻 구현(4) (Insert)

/**
 * KEY를 갖는 node를 생성하여 T에 insert하는 함수.
*/
node_t *rbtree_insert(rbtree *t, const key_t key) {
  node_t *newNode = (node_t *)calloc(1, sizeof(node_t));
  newNode->key = key;

  node_t *parentNode = t->nil;
  node_t *tmp = t->root;
  while(tmp != t->nil) {
    parentNode = tmp;
    if(newNode->key < tmp->key) {
      tmp = tmp->left;
    } else {
      tmp = tmp->right;
    }
  }

  newNode->parent = parentNode;

  if(parentNode == t->nil) {                      // 1. parentNode가 nil인 경우 (newNode가 root)
    t->root = newNode;
  } else if(newNode->key < parentNode->key) {     // 2. newNode가 parentNode의 왼쪽 자식 노드인 경우
    parentNode->left = newNode;
  } else {                                        // 3. newNode가 parentNode의 오른쪽 자식 노드인 경우
    parentNode->right = newNode;
  }

  newNode->right = t->nil;
  newNode->left = t->nil;
  newNode->color = RBTREE_RED;

  rbtree_insert_fixup(t, newNode);

  return newNode;
}

삽입 후 복구

insert가 완료된 후, RBTREE의 특성을 복구하기 위한 insert_fixup이 수행된다.

현재 노드를 기준으로 삼촌 노드를 정의하게 되는데
관계도는 아래와 같다.

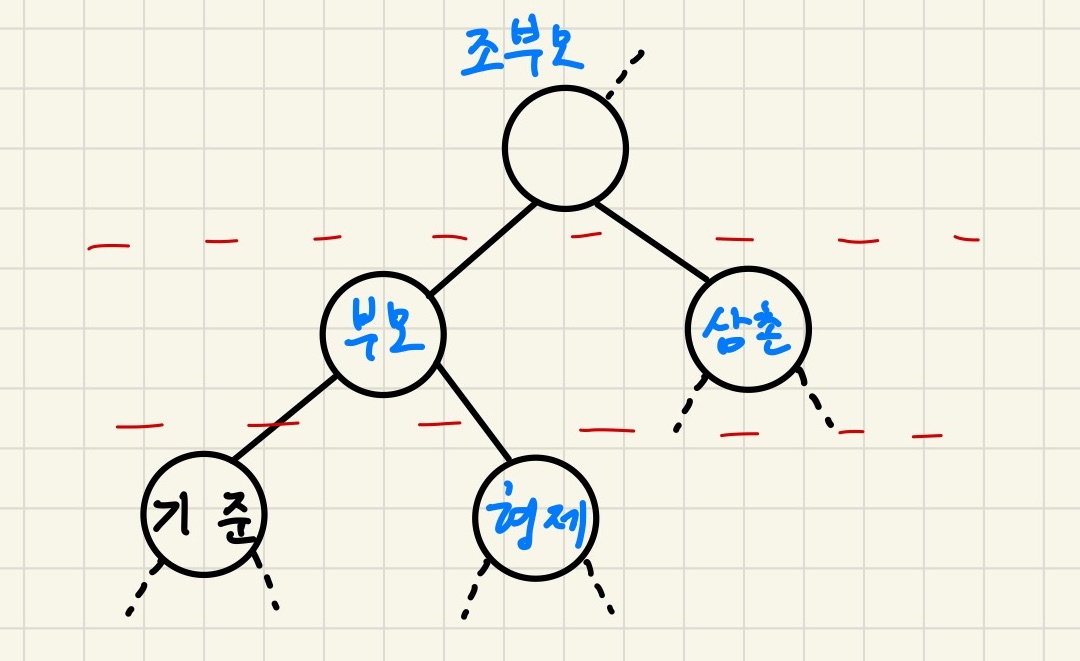
그림처럼, 부모 노드의 형제 노드를 삼촌이라고 부를 예정이다.

insert_fixup이 진행되는 경우는 총 6가지로, 아래 그림과 같다.

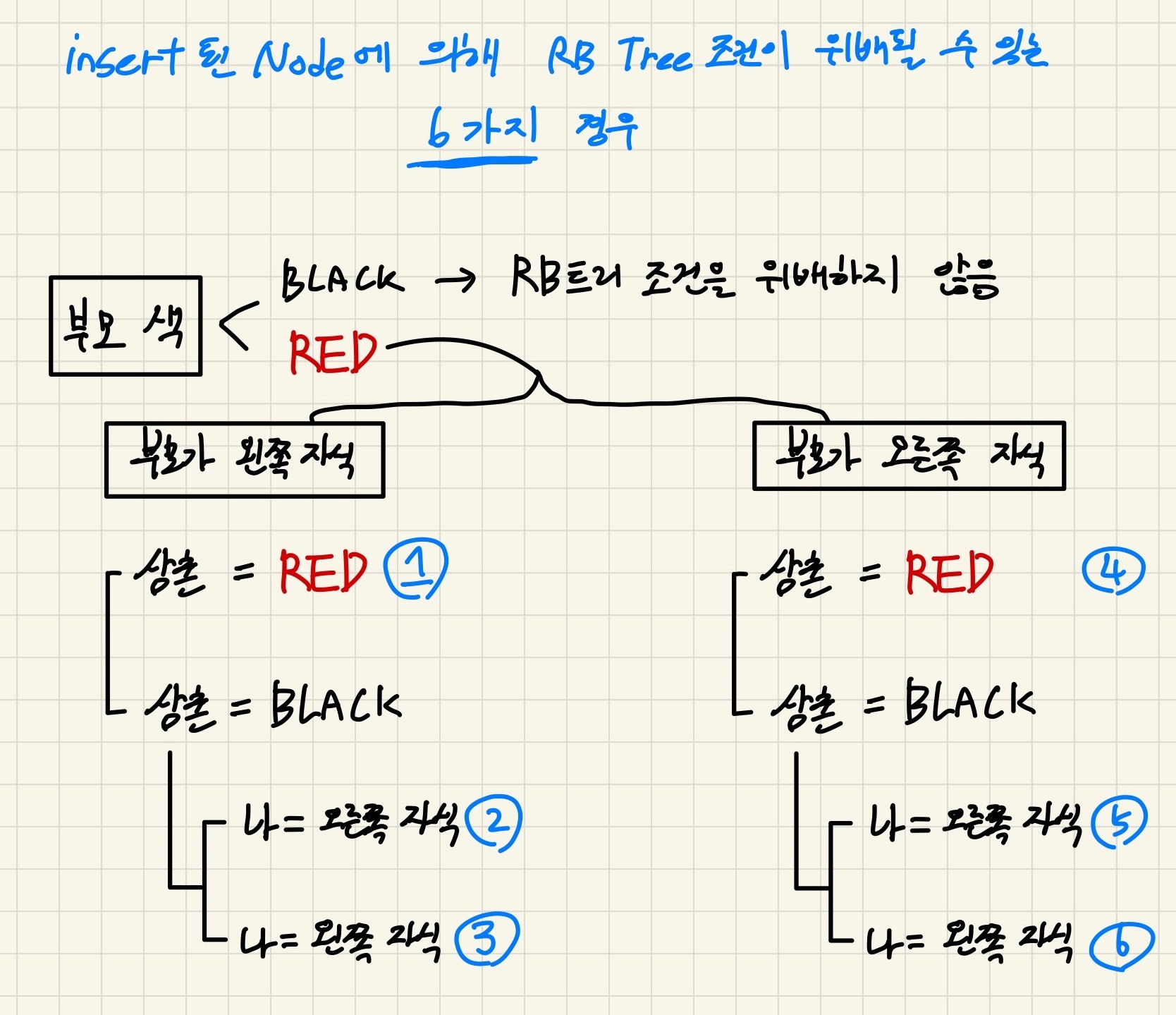
왜 경우가 6가지일까

조건을 다시 보자.

1. 모든 노드는 RED 또는 BLACK

2. 루트는 BLACK

3. 모든 리프(NIL)는 BLACK

4. 노드가 RED 이면 그 노드의 자식은 모두 BLACK

5. 각 노드로부터 그 노드의 자손인 리프로 가는 경로들은 모두 같은 수의 BLACK 노드를 포함해야함

insert된 node인 x(x의 color는 RED)에 의해
RBTREE의 특성이 위배될 수 있는 상황이 존재한다.

조건 1, 3, 5는 insert에 의해 위배되지 않는다.
조건 2, 4는 위배 될 수 있다.

두 조건이 위배되는 경우 모두 x가 RED 이기 때문이며, 각각의 경우는

• 조건 2가 위배되는 경우: x가 루트인 경우
• 조건 4가 위배되는 경우: x의 부모가 RED 인 경우

인 상태일 때 위배된다.

조건 2가 위배되는 경우(x가 루트인 경우)

x의 color를 BLACK 으로 바꿔준다.

조건 4가 위배되는 경우(x의 부모가 RED인 경우)

는 2가지 경우로 구분된다.

1. x의 부모 노드가 조부모 노드의 왼쪽 자식일 경우
2. x의 부모 노드가 조부모 노드의 오른쪽 자식일 경우

또한 2가지의 각 경우는, 또다시 아래와 같은 3가지 경우로 구분된다.

1). x의 삼촌 노드가 RED인 경우
2). x의 삼촌 노드가 BLACK이면서 x가 오른쪽 자식인 경우
3). x의 삼촌 노드가 BLACK이면서 x가 왼쪽 자식인 경우

따라서 먼저 구분된 2가지 경우와 각 경우에서 또 3가지 경우가 존재하므로,
총 6가지 경우에 대한 판단과 각 경우의 해소(RBTREE를 유지 시키는)방법이 존재한다.

💻 구현(5) (insert fix up)

void rbtree_insert_fixup(rbtree *t, node_t *n) {
  while(n->parent->color == RBTREE_RED) {
    if(n->parent == n->parent->parent->left) {
      node_t *uncle = n->parent->parent->right;
      if(uncle->color == RBTREE_RED) {
        n->parent->color = RBTREE_BLACK;
        uncle->color = RBTREE_BLACK;
        n->parent->parent->color = RBTREE_RED;
        n = n->parent->parent;
      } else {
        if(n == n->parent->right) {
          n = n->parent;
          left_rotate(t, n);
        }
        n->parent->color = RBTREE_BLACK;
        n->parent->parent->color = RBTREE_RED;
        right_rotate(t, n->parent->parent);
      }
    } else {
      node_t *uncle = n->parent->parent->left;
      if(uncle->color == RBTREE_RED) {
        n->parent->color = RBTREE_BLACK;
        uncle->color = RBTREE_BLACK;
        n->parent->parent->color = RBTREE_RED;
        n = n->parent->parent;
      } else {
        if(n == n->parent->left) {
          n = n->parent;
          right_rotate(t, n);
        }
        n->parent->color = RBTREE_BLACK;
        n->parent->parent->color = RBTREE_RED;
        left_rotate(t, n->parent->parent);\
      }
    }
  }
  t->root->color = RBTREE_BLACK;
}