문제

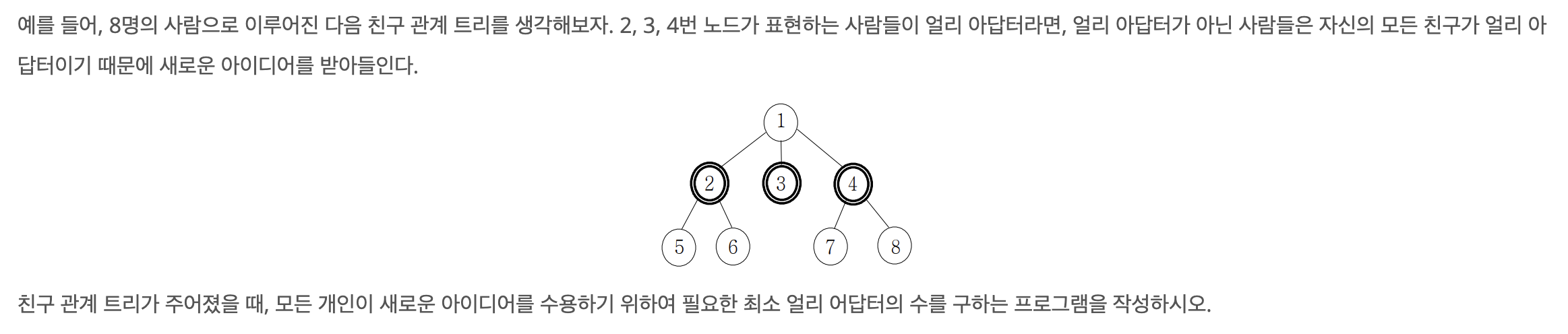
풀이
처음에는 노드를 홀수레벨 노드/짝수레벨 노드 그룹으로 구분해서
한 그룹의 노드만 색칠해 주면 되지 않을까 했지만,
문제의 2번 입출력 예제만 봐도 그렇지 않다는 것을 알 수 있었다.
내가 모르는 유형인 것 같아 풀이를 찾아봤고, tree dp라는 유형의 문제라는 것을 알게되었다.
풀이1. tree DP
일반인 / 얼리어답터는 각각 독립적인 상태이다.
트리의 노드가 일반인인 경우와 얼리어답터인 경우
2가지의 경우의 수를 dp로 모두 구해주면 된다.
dp 테이블은 다음과 같이 정의했다.
dp[node][0]: node가 얼리어답터인 경우, node를 포함한 서브트리의 얼리어답터 수의 최소값
dp[node][1]: node가 일반인인 경우, node를 포함한 서브트리의 얼리어답터 수의 최소값
현재노드가 일반인인 경우, 자식노드는 항상 얼리어답터이어야 하므로
dp[현재노드][1] += dp[자식노드][0] 이다.
그러나 현재노드가 얼리어답터인 경우, 자식노드가 일반인인 경우와 얼리어답터인 경우 중 어떤 경우가 최적해인지 알 수 없다. 따라서 둘 중 작은 값으로 현재노드를 갱신해주어야 한다.
dp[현재노드][0] += min(dp[자식노드][0], dp[자식노드][1])
대략적인 흐름은 아래와 같다.
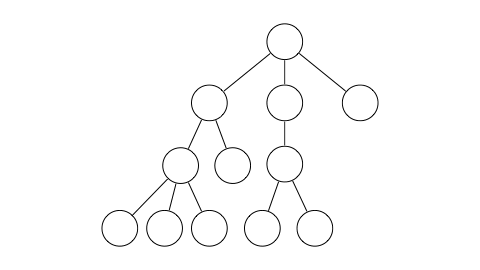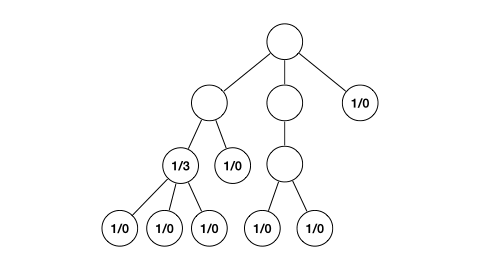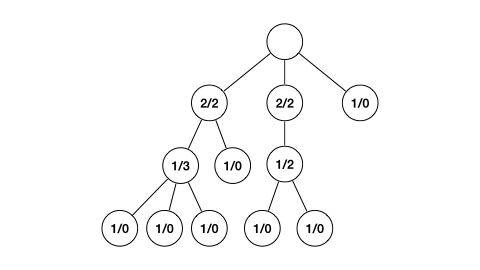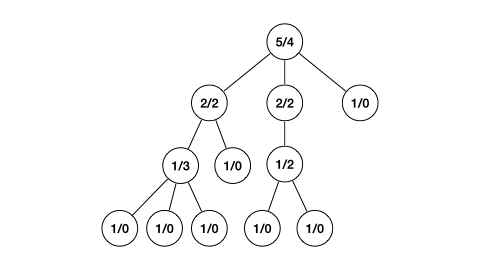
이 그림의 순서는 dp 테이블이 갱신되는 순서와 같지 않다.
코드 이해하기
코드
421204kb 5836ms
def solution(tree):
answer = 0
root = 1
# tree_dp[node][0]: node가 얼리어답터인 경우 node를 포함한 서브트리의 얼리어답터 수
# tree_dp[node][1]: node가 일반인인 경우 node를 포함한 서브트리의 얼리어답터 수
tree_dp = dict()
dfs(root, tree_dp, tree)
answer = min(tree_dp[root][0], tree_dp[root][1])
return answer
def dfs(current, tree_dp, tree):
# 처음 방문시, 현재 노드가 얼리어답터 인 경우의 수를 포함해 초기값을 저장한다.
if current not in tree_dp:
tree_dp[current] = [0, 0]
tree_dp[current][0] = 1
for adjacent_node in tree[current]:
# adjacent_node가 current의 부모노드 인 경우도 존재함
# 따라서 방문하지 않은 노드를 확인하기 위해 tree_dp의 key로 존재하는지를 확인
if adjacent_node not in tree_dp:
dfs(adjacent_node, tree_dp, tree)
# 현재 노드가 얼리어답터 인 경우, 자식 노드가 얼리어답터, 일반인 중 어떤 경우일 때 최적해가 나오는지 알 수 없다.
tree_dp[current][0] += min(tree_dp[adjacent_node][0], tree_dp[adjacent_node][1])
# 현재 노드가 일반인인 경우, 자식 노드는 항상 얼리어답터이어야 한다.
tree_dp[current][1] += tree_dp[adjacent_node][0]풀이2. 그리디
이 풀이는 간선이 하나뿐인 노드(트리의 모든 리프 노드 + 루트 노드가 포함될수도 있다.)부터 시작해서 얼리어답터를 특정하고, 그 노드의 간선을 제거해가며 다시 일반인 노드를 구하는 방식이다.
tree dp가 아닌 방식으로 푼 코드를 보고나서 도대체 이게 왜 되는지 잘 이해가 되지 않아, 공부한 내용을 정리하고자 적는 풀이이다.
먼저 코드를 보면서 어떤 순서로 문제를 해결하는지 이해해 보았다.
코드 이해하기
코드
입출력 하는 부분을 제외하고 로직만 나타낸 코드이다.
두 매개변수 edge와 n은 각각 아래와 같은 데이터가 저장되어있다.
edge: 2차원 리스트. 인접 리스트 형태로 간선 정보가 저장됨
n: 정수. 트리를 구성하는 노드 갯수
또한, solution 함수 내부에서 선언된 몇가지 변수의 역할은 다음과 같다.
early_adopter: 얼리어답터 노드를 저장할 set
visited: 노드의 방문 체크 리스트
stack: 간선의 갯수가 1이하인 정점들만 들어갈 스택
stack의 역할은 해당 풀이에서 가장 핵심적이다. 정확히 어떤 역할을 하는지는 아래에서 코드를 풀어보며 알아보자.
def solution(edge, n):
early_adopter = set()
visited = [False] * (n+1)
stack = []
for i in range(1, n+1):
if len(edge[i]) == 1:
stack.append(i)
while stack:
cur = stack.pop()
if(visited[cur]): continue
sVertex = edge[cur][0]
visited[sVertex] = True
early_adopter.add(sVertex)
_edge = (edge[sVertex])[:] # deepcopy
for v in _edge:
edge[sVertex].remove(v)
edge[v].remove(sVertex)
if len(edge[v]) == 1 and not visited[v]:
stack.append(v)
if len(edge[v]) == 0:
visited[v] = True
return len(early_adopter)전체 로직의 흐름
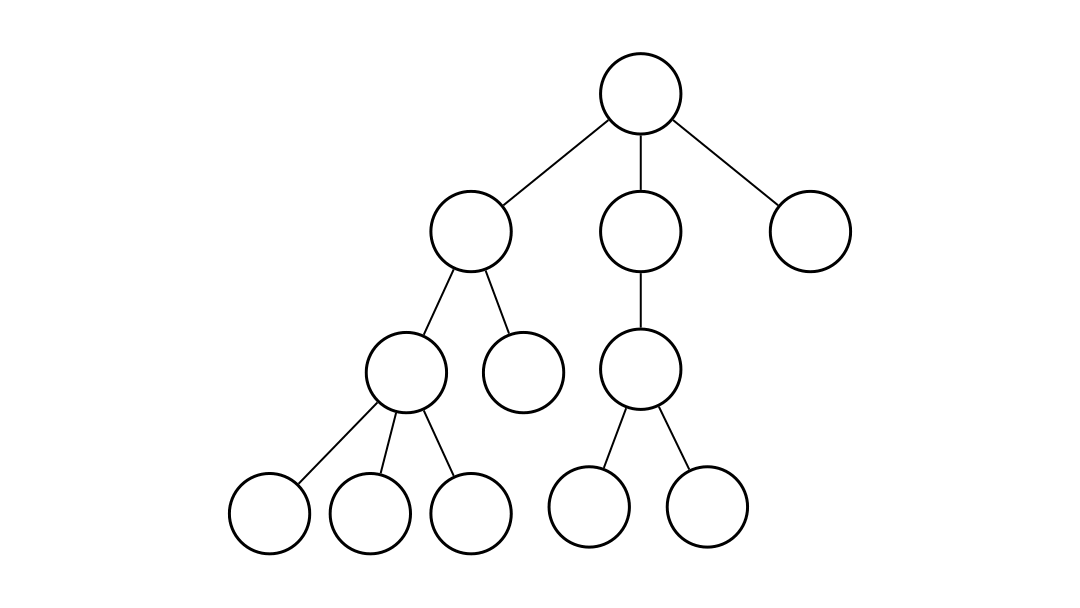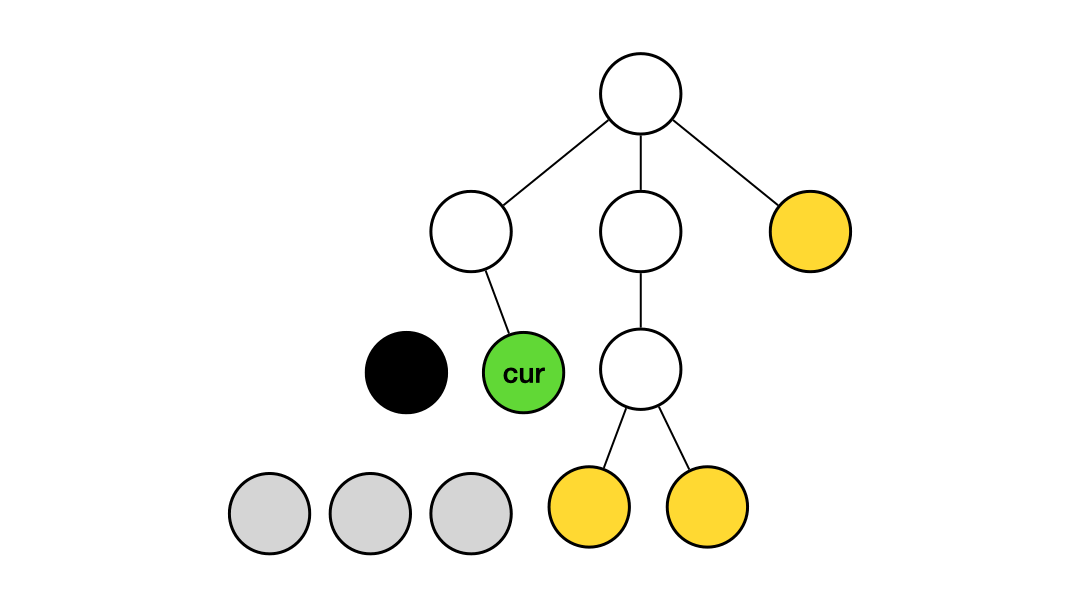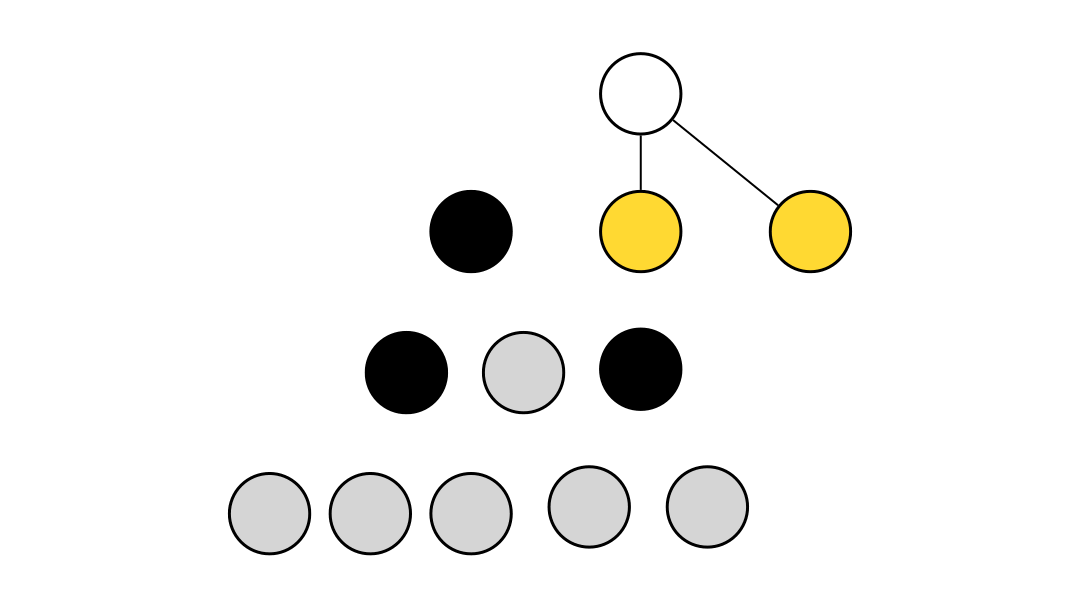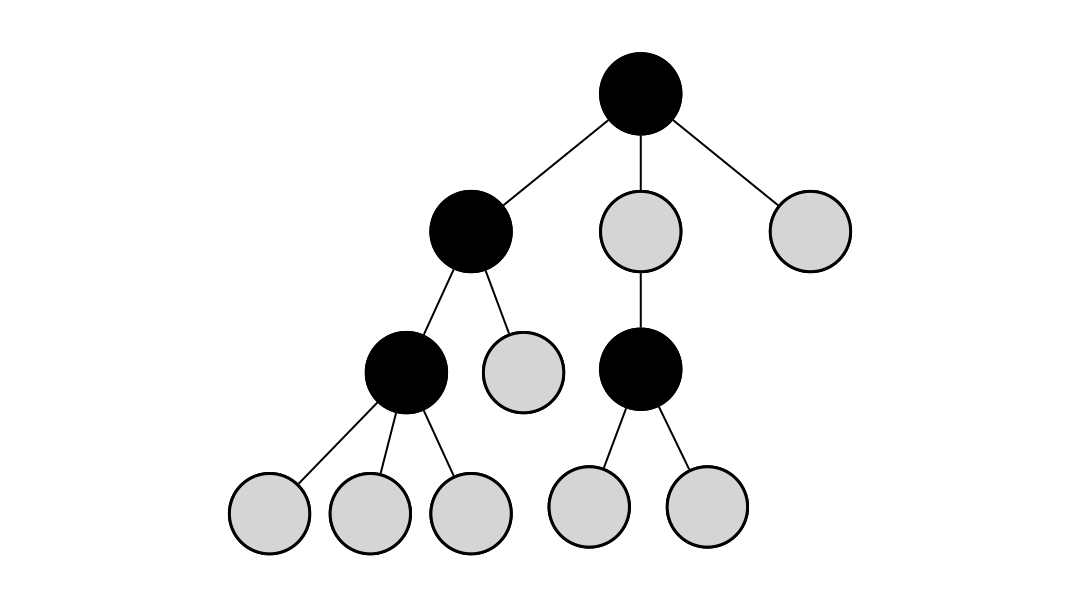
진행 과정을 이해하기 쉽게 gif로 만들어보았다.
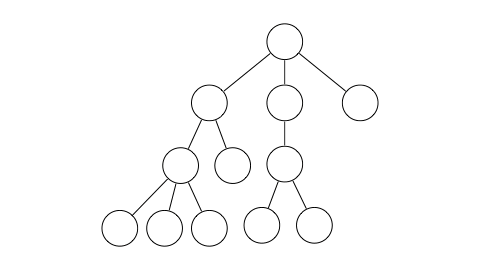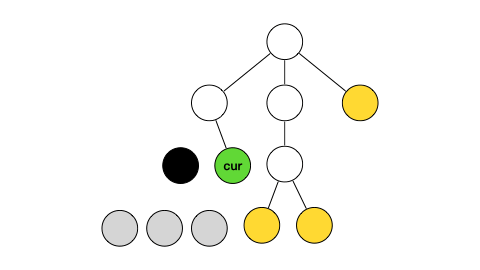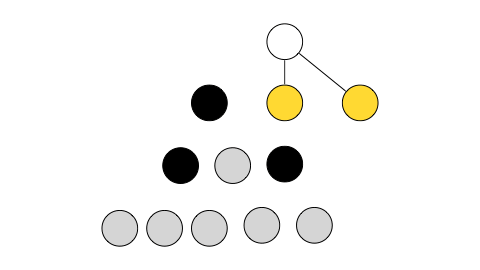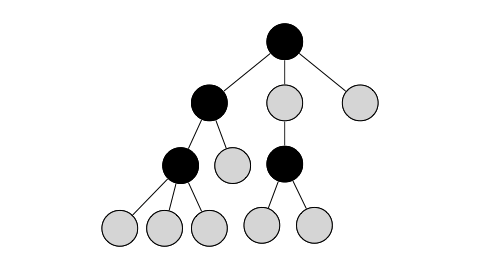
간단하게 설명하면
노란색 노드는 스택에 들어있는 노드,
회색 노드는 모든 연결이 끊긴 노드,
검정색 노드는 얼리어답터로 선택된 노드,
V, cur, SV는 각각 위 코드에서 v, cur, sVertex에 해당하는 노드이다.
위 코드의 흐름을 말로 풀어보면 아래와 같다.
- 연결된 간선이 1개인 정점들을 스택에 저장한다.
- 스택에 원소가 남지 않을 때 까지 아래를 반복한다.
1) 스택에서 노드
cur를 꺼낸다(pop).
2) 꺼낸 노드가 이미 방문한 노드인 경우1)로 돌아간다.
3)cur의 인접 노드인sVertex를 찾아낸다.
4)sVertex를 방문체크 하고early_adopter에 저장한다.
5)sVertex와 인접한 정점v를 순회하며 아래를 반복한다.5-1)
sVertex와v의 인접리스트에서 서로를 각각 삭제하여 두 노드를 잇는 간선을 제거한다.
5-2) 만약v의 남은 간선이 1개이고, 아직 방문하지 않았다면 스택에 저장한다(push).
5-3) 만약v의 남은 간선이 존재하지 않는 경우 방문 체크한다.
early_adopter의 길이를 반환한다.
접근 방법
어떻게 가능할까
이렇게 풀기 위해서 어떤 접근을 했을지 생각해 보았다.
노드 하나가 가질 수 있는 상태는 일반인 또는 얼리어답터 둘 중 하나이다. 그 중 얼리어답터를 특정할 수 있는 상황을 생각해보면, 단 하나의 간선으로 연결된 두개의 정점을 생각해 볼 수 있다. 두 정점 최소 하나는 얼리어답터여야 만이 문제의 조건을 만족하며, 우리는 얼리어답터의 수를 최소로 하는 것이 목표이기 때문에 둘 중 하나만을 얼리어답터 노드로, 다른 하나는 일반인 노드로 만들어주어야 한다.
간선이 하나 뿐인 정점들의 집합 A와 A의 원소인 정점a,
A의 원소들이 연결된 정점들의 집합B, 그리고 a와 연결되었으며 B의 원소인 정점b 를 생각해보자.
b가 A에 속하는 경우는 트리의 전체 노드가 2개 일 때 뿐이며, 그 외의 경우(트리의 노드가 2개보다 많음)에 b는 A에 속하지 않는다. b는 트리의 노드이기 때문에 1개 이상의 간선으로 연결되어있고, 문제의 입력 조건에서 노드의 갯수가 2개 이상으로 주어졌으므로, b의 간선은 트리의 총 노드 갯수가 2개일 때를 제외하고는 항상 2개 이상이다.
그렇다면, 간선이 1개 뿐인 노드a와 2개 이상인 노드b중 "어떤 노드를 얼리어답터로 선택할 때" 최적해에 가까운가?
이 질문을 바꿔 말하면 "집합 A와 집합 B 중 원소가 많은 집합은 어떤것인가?" 가 되겠다.
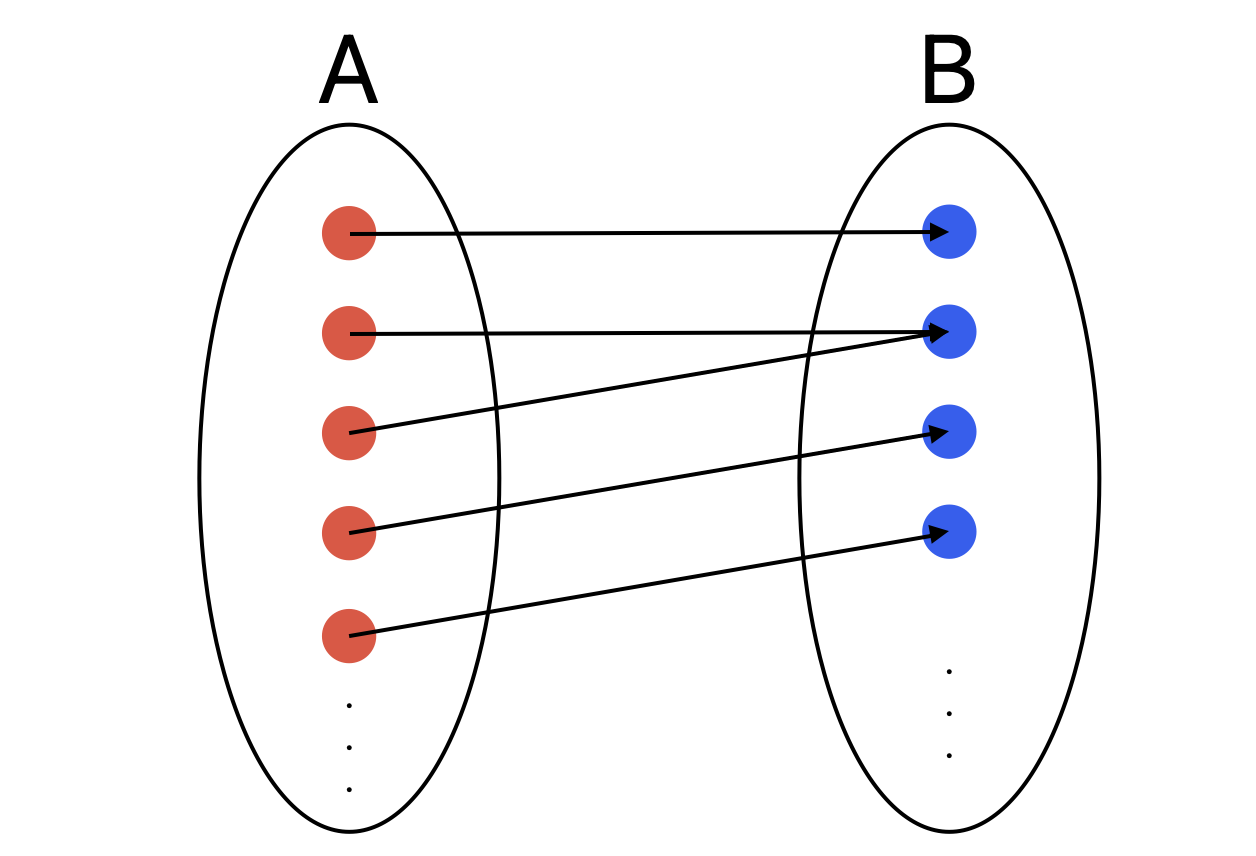
집합 B는 집합 A의 원소와 연결된 정점만을 모아둔 집합이기 때문에, A보다 원소의 갯수가 항상 작거나 같다.
따라서 두 노드 중 하나의 노드를 항상 얼리어답터로 선택해야 할 때, 노드b를 얼리어답터로 선택하는 것이 더 최적해에 가까운 선택이라고 할 수 있다.
그렇기 때문에, 다음과 같은 가정이 가능하다.
가정:
간선이 1개인 정점a와 연결된 정점b중, 정점b를 얼리어답터로 선택하는 것이 항상 최적의 선택이다.
가정에 따라, b의 인접 정점들의 집합 C의 임의의 원소 k는 아래 3가지 경우 중 한가지에 반드시 포함된다.
1).
k의 간선 갯수가 1개
k와 인접한 정점은b가 유일하고,b는 얼리어답터이다.
따라서k는 항상 일반인을 선택하는 것이 최적의 선택이다.
2).
k의 간선 갯수가 2개
k와 인접한 정점 중b가 아닌 정점을v라고 하자.
우리는 조건을 지키면서, 동시에 얼리어답터의 수를 최소로 만들어야 하므로
다음과 같은 2개의 경우를 생각할 수 있다.
v가 얼리어답터라면,k는 일반인이다.
v가 일반인을 선택한다면,k는 얼리어답터이어야 한다.둘 중 어떤 경우가 얼리어답터의 총 인원수를 줄이는, 최적해에 가까운 선택일까?
답은 '둘 다 상관 없음'이다.
v가 얼리어답터일 수 밖에 없다면,k는 항상 일반인을 선택하는 것이 최적의 선택이다.
v가 일반인을 선택할 수 있을 때도v가 얼리어답터를 선택하게 하고,k를 일반인으로 만들어 줄 수 있다.
이렇게 하더라도 전체 얼리어답터수는 변하지 않고,k와 연결된 노드 중b는 얼리어답터 이므로,k가 상태에 영향을 미칠 수 있는 노드는v가 유일하다.
따라서v를 항상 얼리어답터로 만들면,k는 항상 일반인을 선택 할 수 있고,
이는 최적의 얼리어답터수를 구하는데 영향을 미치지 않는 선택이다.
3).
k의 간선 갯수가 3개 이상
k가 얼리어답터, 일반인 중 어떤 것을 선택하는게 최적의 선택인지 알 수 없다.
따라서 k의 간선 갯수가 2개 이하인 경우,k는 일반인을 선택할 수 있다.
로직은 일반인 노드를 간선의 갯수로 특정한다.(간선이 1개인 노드들=일반인 노드)
일반인 노드의 인접 노드는 항상 얼리어답터를 선택 해야한다는 조건을 이용해서 얼리어답터 노드를 특정한다.
그리고 얼리어답터 노드의 모든 간선을 제거하고, 인접 노드의 간선 수를 줄여나간 뒤 다시 조건에 맞는(간선이 1개인)노드를 일반인 노드로 저장한다.
이것이 가능한 이유는 노드 k의 인접 노드 b 가 얼리어답터인 경우, 노드b가 k의 상태(일반인 or 얼리어답터)에 영향을 주지 못하기 때문이다.
간선을 제거해도 인접 노드의 상태를 결정하는것에 영향을 미치지 않기 때문에 계속해서 '간선의 수(1 or 2 or 3이상)로 일반인 노드를 확인'하는 것이 가능하다.
로직 다시 보기
- 연결된 간선이 1개인 정점들을 스택에 저장한다.
간선이 1개인 노드는 얼리어답터가 되지 않아도 되는 노드 즉, 일반인을 선택할 수 있는 노드이다.
이 노드들을 이용해서 얼리어답터가 되어야 하는 노드를 선택한다.
- 스택에 원소가 남지 않을 때 까지 아래를 반복한다.
1) 스택에서 노드
cur를 꺼낸다(pop).
2) 꺼낸 노드가 이미 방문한 노드인 경우1)로 돌아간다.
스택에는 간선이 하나 이하인 노드만 존재한다.
방문 처리는 이후 로직에서 진행되는데, 방문 처리된 노드의 간선을 모두 제거해주는 것을 알 수 있다.
따라서 노드가 이미 방문되었다면, 간선이 제거된 노드일 것이다.
즉, 방문 처리된 노드의 유일한 간선은 이미 제거되고 없으며, 간선이 존재하지 않는 노드이다.
3)
cur의 인접 노드인sVertex를 찾아낸다.
간선이 1개인 노드 cur의 인접노드 sVertex는 cur과 연결된 유일한 인접 노드이다.
4)
sVertex를 방문체크 하고early_adopter에 저장한다.
가정에 따라, sVertex는 얼리어답터를 선택하는 것이 최적의 선택이다.
5)
sVertex와 인접한 정점v를 순회하며 아래를 반복한다.5-1)
sVertex와v의 인접리스트에서 서로를 각각 삭제하여 두 노드를 잇는 간선을 제거한다.
sVertex는 얼리어답터이다. 얼리어답터로 선택된 노드와 인접한 노드들은 위의 설명에서 노드 k에 해당하는 노드들이다.
간선을 제거하는 이유는 얼리어답터노드와 연결된 정점의 상태 결정에 얼리어답터노드가 영향을 미치지 못하기 때문이며, '간선수가 1개 이하인 노드'가 '일반인 노드'라는 조건으로 계속해서 일반인 노드를 찾아낼 수 있기 때문이다.
5-2) 만약
v의 남은 간선이 1개이고, 아직 방문하지 않았다면 스택에 저장한다(push).
5-3) 만약v의 남은 간선이 존재하지 않는 경우 방문 체크한다.
여기서 간선이 존재하지 않는 인접 노드는 원래 간선이 하나이며 sVertex와 연결된 노드이다. 아직 스택에 존재하고 있지만 sVertex의 다른 인접 노드가 먼저 스택에서 나와(cur) sVertex의 인접 노드의 연결을 끊었기 때문에 나중에 스택에서 나와도 간선이 존재하지 않는다.
early_adopter의 길이를 반환한다.
이렇게 early_adopter에 저장된 노드는 모두 얼리어답터이다.
수정된 코드
위의 코드는 다른 사람의 코드를 이해하기 위해 그대로 가져온 것이다.
그런데 로직을 이해하고 보니 방문 체크를 위한 visited 배열이 없어도 된다는 것을 알게되었고, 삭제를 위해 배열을 deepcopy하는 부분도 조금 수정했다. 정답 여부까지 백준에 제출해서 확인하였다.
216536kb 2460ms
def solution(edge, n):
early_adopter = set()
stack = []
# 연결된 edge가 하나인 노드를 stack에 담기
for i in range(1, n+1):
if len(edge[i]) == 1:
stack.append(i)
# stack에는 항상 간선이 1개 이하인 노드만 존재함
while stack:
cur = stack.pop()
if not edge[cur]: continue
sVertex = edge[cur][0]
early_adopter.add(sVertex)
for v in edge[sVertex]:
edge[v].remove(sVertex)
if len(edge[v]) == 1:
stack.append(v)
edge[sVertex] = ()
return len(early_adopter)
if __name__ == '__main__':
import sys
input = sys.stdin.readline
n = int(input())
edge = [[] for _ in range(n+1)]
for _ in range(n-1):
u, v = map(int, input().split())
edge[u].append(v)
edge[v].append(u)
ans = solution(edge, n)
sys.stdout.write(f'{ans}')