[프로그래머스][Python] 도둑질

문제

문제 설명

도둑이 어느 마을을 털 계획을 하고 있습니다. 이 마을의 모든 집들은 아래 그림과 같이 동그랗게 배치되어 있습니다.

각 집들은 서로 인접한 집들과 방범장치가 연결되어 있기 때문에 인접한 두 집을 털면 경보가 울립니다.

각 집에 있는 돈이 담긴 배열 money가 주어질 때, 도둑이 훔칠 수 있는 돈의 최댓값을 return 하도록 solution 함수를 작성하세요.

제한사항

이 마을에 있는 집은 3개 이상 1,000,000개 이하입니다.
money 배열의 각 원소는 0 이상 1,000 이하인 정수입니다.

입출력 예

money	return
[1, 2, 3, 1]	4

---

접근

원형 배열에서의 DP 문제이다.
배열이 원형으로 존재하기 때문에, 첫 선택이 마지막 선택에 영향을 주며
따라서 첫 선택에 따라 여러가지의 경우가 존재한다.

이 문제에서는

• 첫번째 집을 도둑질 할 경우
• 그렇지 않은 경우

2가지로 구분할 수 있으며,
따라서 메모이제이션을 위한 DP테이블은
2가지 경우를 모두 계산하기 위한 2차원 배열로 표현할 수 있다.

dp[0][i]에는 첫번째 집을 도둑질 한 경우 i번째 집을 도둑질 했을때의 훔친 돈의 최대값이,
dp[1][i]에는 첫번째 집을 도둑질하지 않은 경우 i번째 집을 도둑질 했을때의 훔친 돈의 최대값이 갱신된다.

첫번째 집을 도둑질 하지 않는 경우에서 최대값을 구할 수 있는 방법은
두번째 집을 선택하는것이다.
따라서 아래와 같은 2가지 경우로 나타난다.

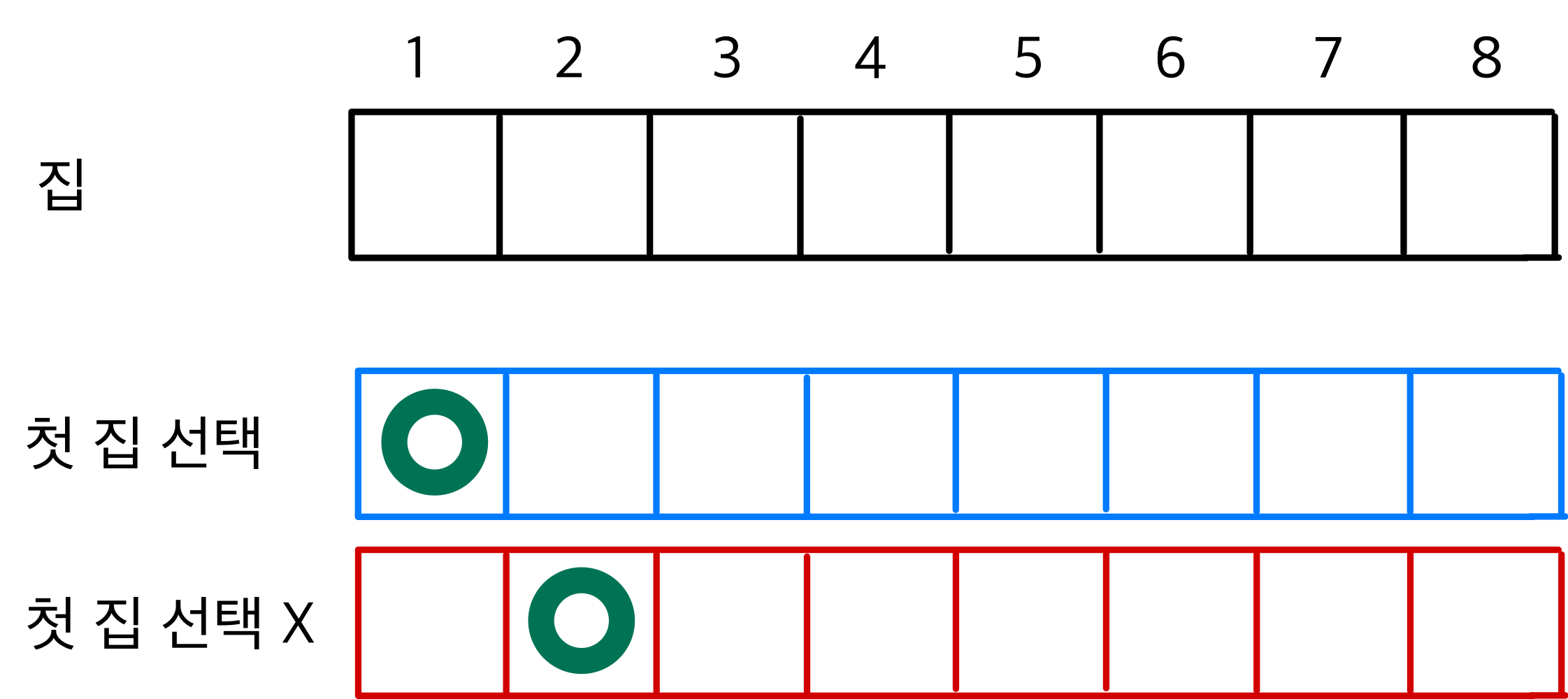
3번 집의 경우,
항상 1번집에서 훔친 돈 + 3번집의 돈이 최대값이며,
따라서 첫 집을 선택한 경우에는 1번집+3번집이,
첫 집을 선택하지 않은 경우에는 3번집의 돈을 그 최대값으로 갖는다.

이후의 집을 도둑질 할 경우에는 2가지 선택이 주어진다.

현재 집이 i번째 집일 때,
1. i-2 번째 집을 도둑질 한 후에 현재 집을 도둑질하는 경우
2. i-3 번째 집을 도둑질 한 후에 현재 집을 도둑질하는 경우

두 경우 중 최대값으로 현재 집의 dp 테이블을 갱신해준다.

마지막에 최대값을 구할 때 다시한번 원형 배열임이 고려되어야 한다.

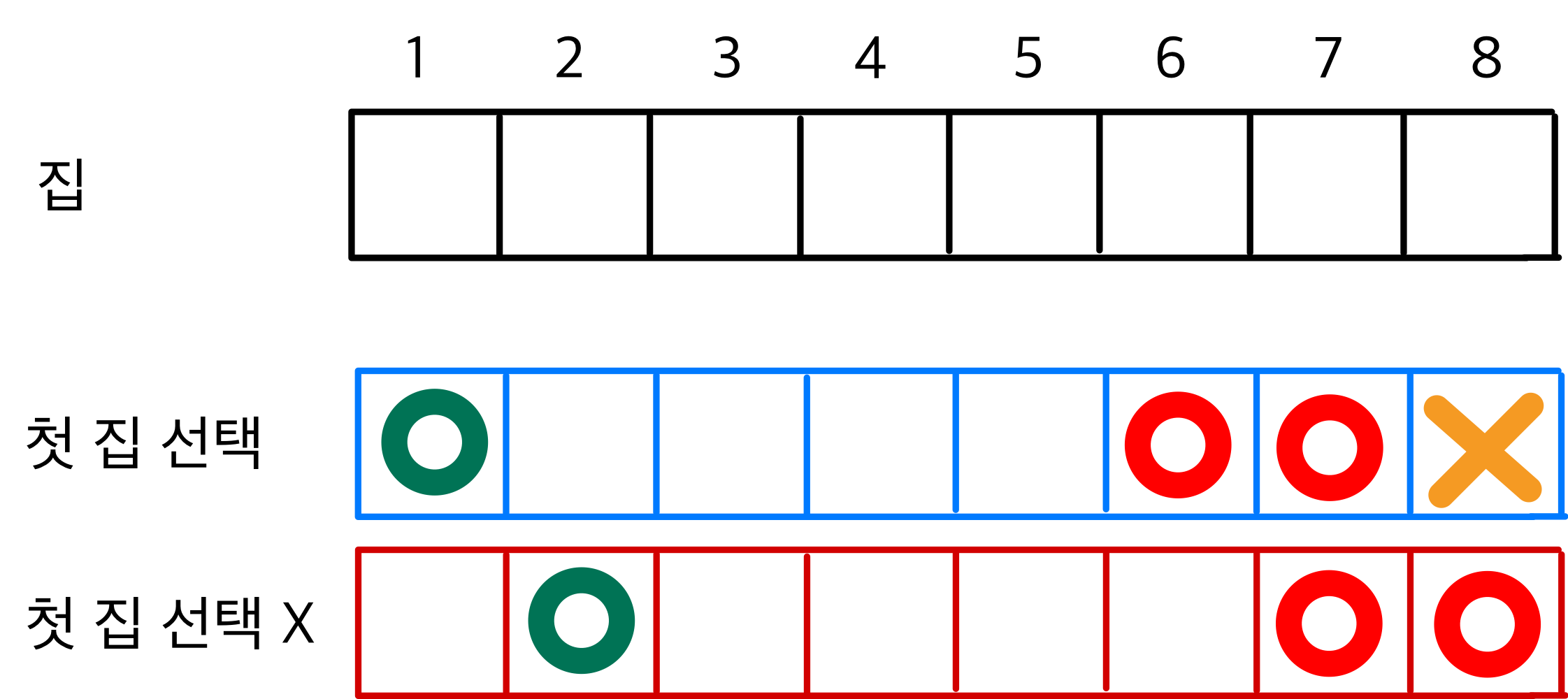
첫 집과 마지막 집은 항상 인접한 집이므로,
첫 집을 선택한 경우에는 항상 마지막 집은 선택하지 못한다.
따라서 마지막-1번째 집(7번집) 또는 마지막-2번째 집(6번집) 중 하나에 최대값이 존재할 것이며,
첫 집을 선택하지 않은 경우는 마지막 집(8번집)과 마지막-1번째 집(7번집) 중에 최대값이 존재한다.

---

코드

def solution(money):
    answer = 0
    N = len(money)
    dp = [[0] * N for _ in range(2)]
    dp[0][0] = money[0]
    dp[1][1] = money[1]
    dp[0][2] = money[2] + dp[0][0]
    dp[1][2] = money[2] + dp[1][0]
    
    for i in range(2, N):
        dp[0][i] = money[i] + max(dp[0][i-2], dp[0][i-3])
        dp[1][i] = money[i] + max(dp[1][i-2], dp[1][i-3])
    answer = max(dp[0][N-2], dp[0][N-3], dp[1][N-2], dp[1][N-1])
    return answer