백준 1004번 어린왕자 이야기
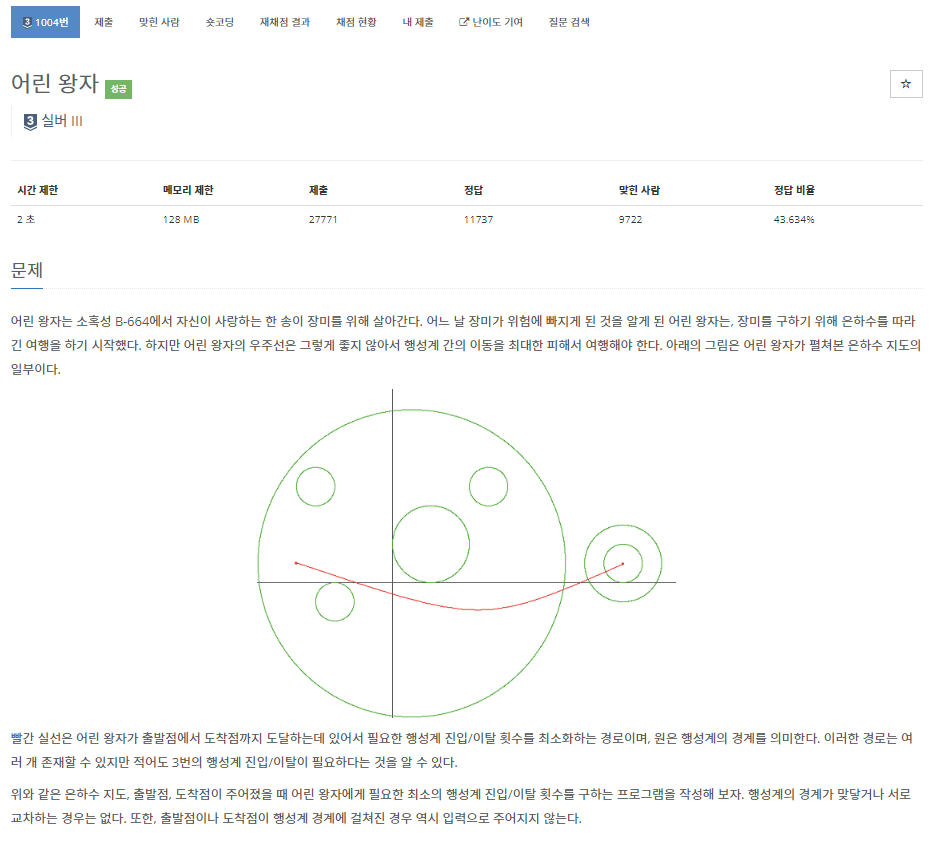
문제
입력 및 출력 값

풀이:
해당 문제의 핵심은 '그림에 속지 말자'이다.
그림을 처음 봤을 때 너무 많은 방법 수가 나오기 때문에 문제에 대해 제대로 이해하지 못했다.
하지만 두 번째 입력 예제의 경우 그림을 그리기엔 너무 많고 수가 큰 걸 알 수 있다. 이는 그림이 아닌 수학적 공식을 활용해야 한다는 뜻이다.
한 원과 두 점이 존재할 때 두 점이 진입/이탈 하는 경우는 딱 한 가지다. 첫 번째 점은 원의 내부에 존재하고, 두 번째 점은 원의 외부에 존재할 때다.
이 때 점이 원의 내부에 존재할 경우는 원의 중심과 점의 거리가 원의 반지름보다 짧다면 내부에, 반지름보다 크다면 원의 외부에 존재한다는 것을 알 수 있다.
코드
testcase = int(input())
for _ in range(testcase):
cnt = 0
x1, y1, x2, y2 = map(int, input().split())
N = int(input())
for i in range(N):
cx, cy, cr = map(int, input().split())
dist1 = (x1 - cx) ** 2 + (y1 - cy) ** 2
dist2 = (x2 - cx) ** 2 + (y2 - cy) ** 2
if (dist1 < cr**2 and dist2 > cr**2) or ( dist1 > cr**2 and dist2 < cr**2):
cnt += 1
print(cnt)dist1 = (x1 - cx) ** 2 + (y1 - cy) ** 2
dist2 = (x2 - cx) ** 2 + (y2 - cy) ** 2
위의 두 거리를 활용해 두 점과 원의 중심사이의 거리를 활용해 문제를 풀었다. 이때 등호를 뺀 이유는 진입과 이탈은 원 밖으로 나가야 하는데 그 경우가 애매하기 때문에 뺐다.
결과

