프로그래머스 Lv0 '분수의 덧셈' 문제를 풀던 때를 기록한 포스트이다.

1. 문제를 처음 접했을 때

자바스크립트로 코테 준비를 하기 위해, 프로그래머스의 Lv0 문제들을 자바스크립트로 풀어보기 시작했다. (코테 준비를 처음 해 보기 때문에 Lv0부터 시작...ㅎ.ㅎ)
문제를 보고 코드를 어떻게 짜야 할 지 도무지 감이 안 잡히던 첫 문제가 바로 Day2의 '분수의 덧셈'이라는 문제였다.
문제를 풀면서 같이 참고하고 있던 '라매개발자' 라는 유튜브를 보면서 문제 접근 방식, 코드를 어떻게 작성 할 지에 대해서 참고할 수 있었다.

2. 문제 풀이

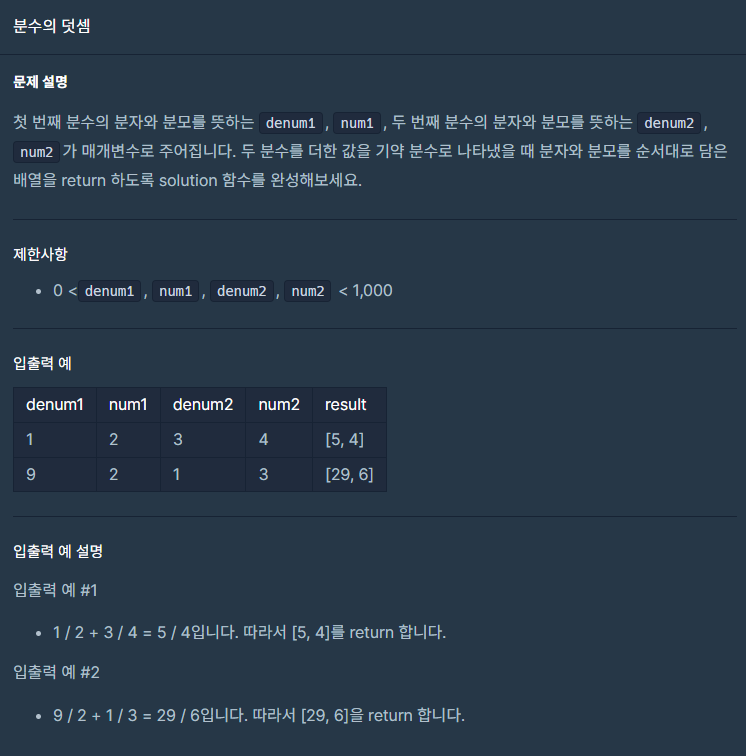
유튜브를 참고하여 내가 문제를 접근 한 방식은 다음과 같다.

• 1. 분모끼리 곱한 값을 결과값의 분모로, (denum1 x num2) + (denum2 x num1) 한 값을 결과값의 분자로 둔다.

---

• 2. 기약분수로 만들어 주기 위해 결과값의 분모, 분자 중 작은 값을 찾아낸다. 이 수를 minNum이라고 하겠다.

---

• 3. 분모와 분자를 각각 minNum으로 나누어 분모, 분자가 각각 나누어 떨어질 때 까지 minNum 값을 -1 한다. (분모, 분자를 minNum으로 나누었을 때 각각 안 나누어 떨어지면 minNum을 -1 해서 다시 나누고, 안 나누어 떨어지면 다시 -1 하고를 반복)

---

• 4. 분모와 분자를 각각 minNum으로 나누었을 때 나누어 떨어진 값들을 배열에 담아 return 한다.

---

총 4단계로 나눌 수 있었다. 그 결과 내가 작성한 코드는

function solution(denum1, num1, denum2, num2) {
    var answer = [];
    
    const denum = (denum1 * num2) + (denum2 * num1);
    const num = num1 * num2;
    // ex) 1/2 + 3/4 = (1*4 + 3*2) / 4*2 = 10/8 을 한 과정
    
    let minNum = (denum < num) ? denum : num;
    // 결과값의 분자와 분모 중 작은 값을 minNum에 넣어줌.
    
    for (let i = minNum; i >= 1; i--) {
        if(denum % i === 0 && num % i === 0) {
            answer.push(denum / i, num / i);
            break;
        }
    }
    // 결과값의 분자와 분모를 i으로 나누었을 때 나누어 떨어진다 ? => i는 최대공약수 (i의 초기값이 minNum이고 조건에 만족 할 때(break이 포함된 if문을 만족 할 때) 까지 -1한다.)
    
    return answer;
}

로 작성 할 수 있었다.

3. 유클리드 호제법

구글링을 하던 중 '유클리드 호제법'이라는 알고리즘을 이용하여 최대공약수를 구하는 것을 알게 됐다.

유클리드 호제법이란 ?
두 수의 최대공약수를 구하는 알고리즘이다.

1. 2개의 자연수 A, B가 주어지고, 둘 중 큰 값이 A라고 가정 했을 때,
2. A를 B로 나눈 나머지를 n이라고 하면 (A % B = n) n이 0일 때, B가 최대공약수이다.
3. 만약 n이 0이 아니라면, A에 B 값을 다시 넣고 n을 B에 대입한 후 다시 위에 2번부터 반복하면 된다.

즉, 유클리드 호제법은 나눗셈을 반복하여 최대공약수를 구할 수 있다.

4. 결론

코테 준비를 처음 해보는 과정에서 Lv0 문제를 풀다가 막혔다는 것이 나 자신에게 많이 실망했다...😂
하지만 코테 알고리즘 문제를 접할 때 다짜고짜 코드부터 치려고 하는 것이 아닌 어떤 문제인지 파악하는 것부터, 어떻게 문제를 풀 것인지, 그것을 코드로 어떻게 옮길 것인지 고민과 생각을 충분히 한 후, 정리가 다 됐을 때 코드를 쳐야 좋은 거구나 라는 것을 깨달을 수 있었다. 체계적인 문제풀이 방법이 수립된 것 같아 더욱 열심히 하고 싶어지는 마음이 생긴다.💪

참고자료

https://haerim95.tistory.com/36
https://blockdmask.tistory.com/53