[백준] 1932번 정수 삼각형 C++

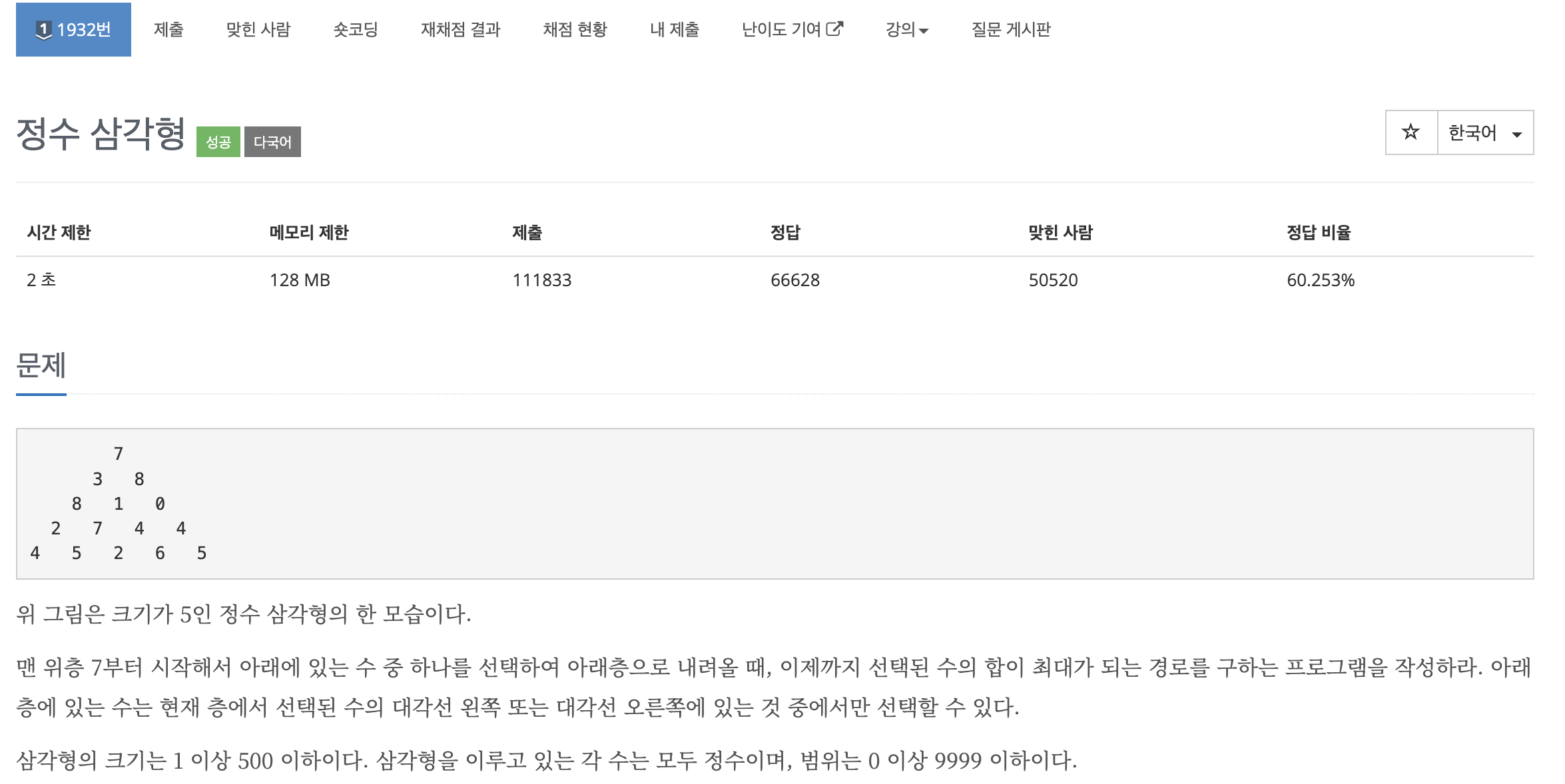
문제 : https://www.acmicpc.net/problem/1932

C++

#include<iostream>
#include<algorithm>
using namespace std;

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    
    int triangle[501][501] = {0,};
    int dp[501][501] = {0,};
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= i; j++) {
            cin >> triangle[i][j];
        }
    }

    dp[1][1] = triangle[1][1];

    for(int i = 2; i <= n; i++) {
        for(int j = 1; j <= i; j++) {
            dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + triangle[i][j];
        }
    }

    int maxNum = dp[n][1];
    for(int i = 2; i <= n; i++) {
        maxNum = max(maxNum, dp[n][i]);
    }
    cout << maxNum << "\n";
}

문제풀이

• 삼각형의 크기를 입력받고 그 크기만큼 정수 삼각형을 입력받는다. 그리고 맨 위층부터 시작해서 왼쪽 아래 혹은 오른쪽 아래를 선택하면서 최종 맨 아래층으로 내려올 때까지의 선택된 수 합이 최대가 되는 경로를 구한다. 문제를 보면서 각 위치에 있는 수가 지금까지 선택된 수의 최댓값을 dp 배열에 저장하면 될 것 같다는 생각을 했다. 그래서 먼저 정수 삼각형을 만들기 위해 이차원 배열을 사용해서 값을 입력받았다. 그런 다음 현재 위치에서 오른쪽 위나 왼쪽 위에 숫자 중 더 큰 숫자를 자신과 더해서 dp배열에 저장했다. 마지막으로 맨 아래 위치의 dp값들 중에서 최댓값을 구하고 출력했다.

Comment

• dp 문제를 풀 때는 크게 Top-Down과 Bottom-Up 방식이 있다. 쉽게 말하면 Top-Down은 재귀로 구현하는 것이고 Bottom-Up은 반복문으로 구현하는 것이다. Top-Down 기법은 값이 큰 것에서 작은 것 순으로 부분 문제를 해결하는 것이고 Bottom-Up 기법은 값이 작은 것에서 큰 것 순으로 부분 문제를 해결하는 것이다. dp 문제를 풀 때는 두 가지 기법을 생각하면서 풀면 더욱 효율적으로 풀 수 있을 것 같다.