[딥러닝/Transformer] 내부 모듈 implementations

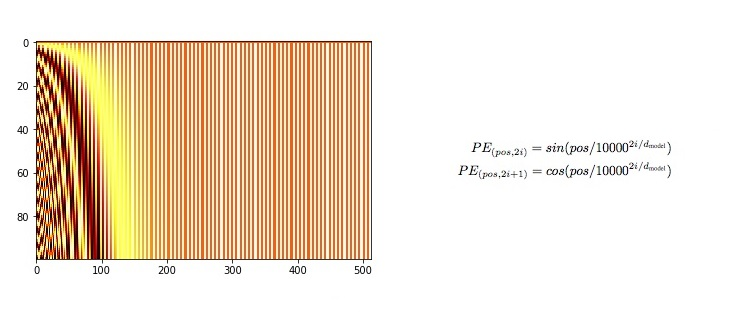
1. Positional Encoding

class PositionalEncoding(nn.Module):

    def __init__(self, d_model, max_len, device):
        
        super(PositionalEncoding, self).__init__()

        self.encoding = torch.zeros(max_len, d_model, device=device)
        self.encoding.requires_grad = False 

        pos = torch.arange(0, max_len, device=device)
        pos = pos.float().unsqueeze(dim=1)

        _2i = torch.arange(0, d_model, step=2, device=device).float()

        self.encoding[:, 0::2] = torch.sin(pos / (10000 ** (_2i / d_model)))
        self.encoding[:, 1::2] = torch.cos(pos / (10000 ** (_2i / d_model)))

    def forward(self, x):
        batch_size, seq_len = x.size()

        return self.encoding[:seq_len, :]

• PositionalEncoding 클래스가 부모 클래스인 nn.module의 초기화 메서드(init) 호출
  - Why? 부모 클래스의 초기화 메서드를 호출하여 부모 클래스가 가진 속성들을 초기화할 수 있음. 이는 부모 클래스에서 정의된 초기화 작업을 자식 클래스에서도 수행해야 할 때 중요
  • 코드 중복 줄여, 유지보수를 용이
  • 다중 상속의 경우, 모든 부모 클래스의 초기화 메서드가 올바른 순서로 호출(MRO)
• 'super()' 자식 클래스가 부모 클래스의 메서드를 오버라이드(재정의)하면서도 부모 클래스의 메서드를 그대로 사용할 수 있게한다. 자식 클래스에서 부모 클래스의 메서드를 명시적으로 호출 가능.
• self.encoding 이라는 [max_len,d_model] 텐서 생성 -> 입력 행렬과 더해져서 같은 크기
• 이 텐서의 gradient를 계산할 필요가 없으므로 'requires_grad'를 false
• 위치 인코딩을 계산하기 위해 위치(pos) 와 인덱스(_2i) 를 초기화
  - pos 는 [0,max_len) 범위의 값을 가지며, 각 단어의 위치를 나타냄.

순서를 알아보자!!
1. (max_len, d_model) 크기의 텐서를 생성 후, 최대 시퀀스 길이와 임베딩 차원 크기를 갖는다. 이 텐서는 학습 중에 학습 중에 업데이트 되지 않는다.
self.encoding = torch.zeros(max_len, d_model, device=device)
self.encoding.requires_grad = False
2. pos = [0,1,2,...,max_len-1] 형태의 위치 인덱스를 생성한다. 1차원 인덱스를 (max_len,1) 크기로 변환한다.
pos = torch.arange(0, max_len, device=device)
pos = pos.float().unsqueeze(dim=1)
3. _2i = [0,2,4,...,d_model-2] 형태의 차원 인덱스를 생성한다.
_2i = torch.arange(0, d_model, step=2, device=device).float()
4. 짝수 인덱스는 sin, 홀수 인덱스는 cos 함수 적용. 이러한 방식으로 각 위치 인덱스에 대해 고유한 주기적 패턴을 갖는 값을 생성한다.
self.encoding[:, 0::2] = torch.sin(pos / (10000 (_2i / d_model)))
self.encoding[:, 1::2] = torch.cos(pos / (10000 (_2i / d_model)))
5. 입력 x 의 크기를 가져와서 batch_size 와 seq_len 정의하고, seq_len에 해당하는 positional encoding 값을 반환한다. 이는 입력 시퀀스의 길이에 맞춰 positional encoding을 잘라서 반환한다.

질문!!
Q. encoding[:, 0::2] 의 문법에 대해서 좀 더 알아보자
A. 텐서의 슬라이싱으로 ':'는 첫 번째 차원(행)을 전체 선택. '0::2' 는 두번 째 차원(열)을 인덱스 0부터 시작하여 2 간격으로 선택

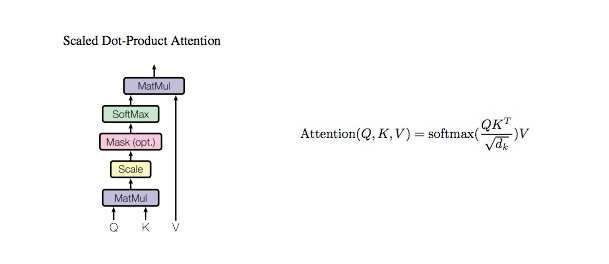
2. Scaled Dot-Product Attention

class ScaleDotProductAttention(nn.Module):

    def __init__(self):
        super(ScaleDotProductAttention, self).__init__()
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, q, k, v, mask=None, e=1e-12):

        batch_size, head, length, d_tensor = k.size()
        k_t = k.transpose(2, 3) 
        score = (q @ k_t) / math.sqrt(d_tensor)  
        
        if mask is not None:
            score = score.masked_fill(mask == 0, -10000)
        
        score = self.softmax(score)

        v = score @ v

        return v, score

• Q,K,V 는 무조건 (batch_size, seq_length, d_model)
  Q = torch.rand(64, 10, d_model)
  K = torch.rand(64, 10, d_model)
  V = torch.rand(64, 10, d_model)
  mask = None

• 배치 크기가 너무 작으면 적은 데이터로 가중치가 자주 업데이트 되어 노이즈 많아 불안정

• 배치 크기가 너무 크면 한번에 처리하는 양이 많아 학습 속도 느려지고 메모리 부족 문제

• 에폭이 너무 크면 overfitting, 너무 작으면 underfitting

• d_model % num_heads == 0
  -> d_model 이 num_heads 로 나누어 떨어져야 각 헤드의 차원 d_k 이 정수가 된다. 그렇지 않으면헤드의 차원이 정수가 되지 않아 어텐션을 계산하는 데 문제가 발생한다. ex) d_model = 512, num_heads = 8 이라고 가정하면 헤드는 차원(d_k)이 64인 벡터를 사용한다.

순서를 딱 정리해보겠다.
1. Q와 K의 전치를 Matmul 계산 후 d_tensor의 제곱근으로 나누어 스케일링한다
k_t = k.transpose(2, 3)
score = (q @ k_t) / math.sqrt(d_tensor)
2. 마스크가 주어져 있을 때만 마스크가 0인 위치의 점수를 매우 작은 값으로 설정하여 소프트 맥스 함수가 해당 위치의 가중치를 무시.
if mask is not None:
score = score.masked_fill(mask == 0, -10000)
3. 위의 스코어 값에 소프트맥스 함수 계산
4. 값에 Value 값과 Matmul 후 값 리턴

질문!!!
Q. batch_size, head, length, d_tensor 를 k.size() 가져와서 정의하는 이유? batch_size, head, length 는 코드에서 쓰이지도 않는데 필요한가?
A. 입력 텐서의 크기를 명확히 하기 위함. 코드의 가독성과 유지 보수성을 높이기 위해 유용하다. 쓰이지는 않지만 입력 텐서의 구조를 명확히 알 수 있고, 향후 디버깅이나 코드 이해에 도움이 된다.
Q. q.size() 사용하면 안되나?
A. Q,K,V 텐서는 동일한 크기를 가진다. 그 중 하나를 가져온다.어느 하나의 크기를 가져와도 상관 없다. k.size()를 사용하는 이유는 Key 텐서가 어텐션 매커니즘에서 중요한 역할을 하기 때문에 이를 기준으로 크기를 가져오는 것이 관례적이다.
Q. 스케일링의 의미
A. dot-product 의 결과값이 크면 소프트맥스 함수에 넣었을 때 매우 큰 값이 되어, 그라디언트가 작아지는 문제가 발생할 수 있다. 이를 방지하기 위해서 d_k의 제곱근으로 나누어 스케일링하여 안정된 학습을 목적으로 한다. 추가로 Q,K의 유사도를 더 잘 반영한다. 차원의 크기에 따라 값이 크게 달라지는 것을 방지한다. \sqrt {d_k} 는 스케일링 인자
Q. 마스크를 사용하는 이유?
A. 마스크는 입력 시퀀스의 유효한 부분과 무시할 부분을 나타낸다. 마스크된 위치(값이 0)의 점수를 매우 작은 값으로 설정하여, 소프트맥스 계산에 무시되도록 한다. 이는 어텐션 매커니즘이 패딩된 부분이나 특정 조건을 만족하지 않는 부분을 고려하지 않도록 하기 위함. 이 과정을 통해 어텐션 매커니즘이 유효하지 않은 정보에 영향을 받지 않고, 올바른 위치에만 집중할 수 있게 한다.
ex)
시퀀스 길이가 5인 두 개의 입력 시퀀스.[1,2,3,4,5], [6,7,8]
이를 표한하는 마스크 텐서 [1,1,1,1,1], [1,1,1,0,0]
어텐션 점수 [0.1, 0.2, 0.3, 0.4, 0.5], [0.6, 0.7, 0.8, 0.9, 1.0]
마스크를 적용하면 [0.1, 0.2, 0.3, 0.4, 0.5], [0.6, 0.7, 0.8, -10000, -10000]
결과적으로 마스크된 위치의 값은 거의 0에 가까운 값을 가지게 된다.

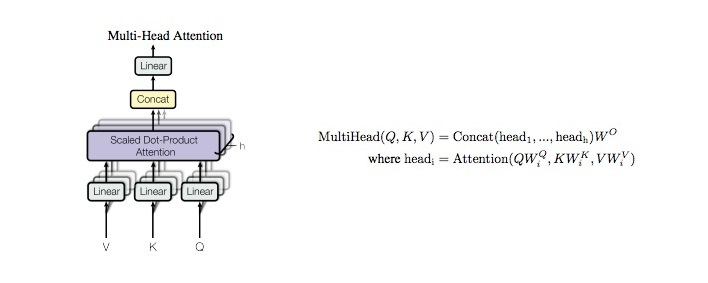
3. Multi-Head Attention

class MultiHeadAttention(nn.Module):

    def __init__(self, d_model, n_head):
        super(MultiHeadAttention, self).__init__()
        self.n_head = n_head
        self.attention = ScaleDotProductAttention()
        self.w_q = nn.Linear(d_model, d_model)
        self.w_k = nn.Linear(d_model, d_model)
        self.w_v = nn.Linear(d_model, d_model)
        self.w_concat = nn.Linear(d_model, d_model)

    def forward(self, q, k, v, mask=None):

        q, k, v = self.w_q(q), self.w_k(k), self.w_v(v)

        q, k, v = self.split(q), self.split(k), self.split(v)

        out, attention = self.attention(q, k, v, mask=mask)
        
        out = self.concat(out)
        out = self.w_concat(out)


        return out

    def split(self, tensor):
       
        batch_size, length, d_model = tensor.size()

        d_tensor = d_model // self.n_head
        tensor = tensor.view(batch_size, length, self.n_head, d_tensor).transpose(1, 2)

        return tensor

    def concat(self, tensor):
        
        batch_size, head, length, d_tensor = tensor.size()
        d_model = head * d_tensor

        tensor = tensor.transpose(1, 2).contiguous().view(batch_size, length, d_model)
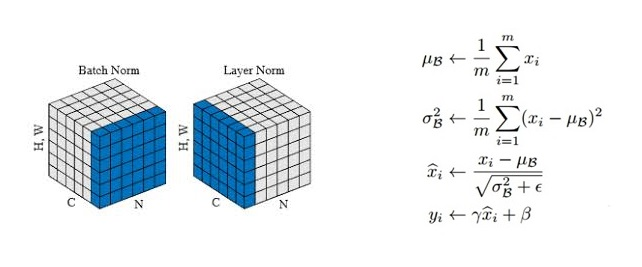
        return tensor

3. Layer Norm

class LayerNorm(nn.Module):
    def __init__(self, d_model, eps=1e-12):
        super(LayerNorm, self).__init__()
        self.gamma = nn.Parameter(torch.ones(d_model))
        self.beta = nn.Parameter(torch.zeros(d_model))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        var = x.var(-1, unbiased=False, keepdim=True)

        out = (x - mean) / torch.sqrt(var + self.eps)
        out = self.gamma * out + self.beta
        return out

순서 정리
1. mean과 var는 입력 데이터 x 의 마지막 차원에 대한 평균 분산 계산 후 결과의 차원을 유지한다. 예를 들어, x = [batch_size, seq_len, d_model] 크기의 텐서라면, d_model 차원에 대한 평균 계산. keepdim = True 는 계산된 평균의 차원을 유지한다는 뜻. 즉 결과 텐서의 크기는 [batch_size, seq_len, 1] 이 된다. 이는 원래 차원을 유지하면서도 브로드캐스팅이 가능하도록 함.
var 의 unbiased=False 는 표본 분산 대신 모집단 분산을 계산하는 데 사용. 분산 계산 시 N 대신 N-1 로 나누지 않음을 의미한다
mean = x.mean(-1, keepdim=True)
var = x.var(-1, unbiased=False, keepdim=True)
2. 정규화 과정. x - mean 은 입력 데이터 x 에서 평균 mean 을 뺀 값. torch.sqrt(var+self.eps)는 분산 var 에 작은 값 eps 를 더한 후 제곱근을 계산한 값(eps 는 분모가 0이 되는 것 방지). 결과적으로 out 값은 입력 데이터를 정규화하여 평균 0, 분산 1로 변환한다.
out = (x - mean) / torch.sqrt(var + self.eps)
out = self.gamma * out + self.beta

질문!!
Q. self.gamma, self.beta 사용 이유?
A. Layer Normalization 의 중요한 매개변수이다. 이 두 개는 정규화된 데이터에 대해 스케일(확장) 및 시프트(이동)를 수행하는 역할을 한다. 이로 인해 정규화 후에도 모델이 충분한 표현력 유지 가능.
gamma 는 d_model 크기의 텐서로 초기값 = 1. 각 입력의 차원의 스케일을 조정하는 역할
beta 는 d_model 크기의 텐서로 초기값 = 0. 각 입력 차원의 시프트를 조정하는 역할
nn.Parameter 로 정의된 gamma,beta 는 학습 가능한 매개변수로 설정되어, 학습 과정에서 업데이트
Q. Layer Norm의 궁극적인 목적
A. 신경망의 학습을 안정화하고, 학습 속도 높이고, 더 나은 일반화 성능을 제공하는 것. 이를 통해 각 층(layer)에서의 입력 분포를 일정하게 유지하여 신경망의 깊이가 깊어질수록 발생할 수 있는 학습의 어려움을 줄여줌.
Q. 스케일(gamma) 조정의 이유 및 효과?
A. Layer Norm 을 통해 입력 데이터는 평균 0,분산 1인 정규 분포로 변환된다. 그러나 모든 데이터가 동일한 분포를 가지게 되면, 특정 특성이 과도하게 억제될 수 있다. 모델의 각 뉴런이 입력 특성의 상대적 중요도를 학습할 수 있도록 정규화된 값에 대해 개별적인 스케일 조정이 필요. 이를 통해 뉴런이 다영한 크기의 출력을 가질 수 있어 모델의 표현력 유지가 가능하다.
Q. 시프트(beta) 조정의 이유 및 효과?
A. 정규화된 데이터는 평균 0 조정되기 때문에, 이로 인해 뉴런의 출력이 비선형 활성화 홤수(ReLU)를 통과할 때 모두 동일한 중심점을 가질 수 있다. 입력 데이터의 특성에 맞춰 출력 값을 적절히 이동시킬 필요가 있다. 이를 통해, 비선형 활성화 함수가 입력의 다양성을 반영할 수 있고, 뉴런의 출력이 동일한 값을 가지는것 방지, 학습 안정성 향상
Q. 결국엔 Layer Norm 은 왜 써?
A. 학습 안정화,학습 속도 향상, 데이터의 불규칙성 감소하여 일반화 성능 제공. 각 데이터 포인트에 대해 독립적으로 정규화를 수행하므로, 배치 크기에 독립적.

4. Positionwise Feed Forward

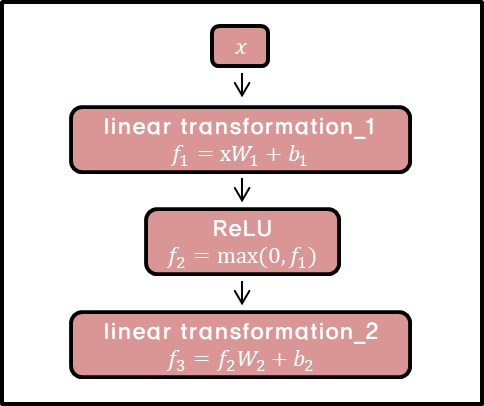
class PositionwiseFeedForward(nn.Module):

    def __init__(self, d_model, hidden, drop_prob=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.linear1 = nn.Linear(d_model, hidden)
        self.linear2 = nn.Linear(hidden, d_model)
        self.relu = nn.ReLU()
        self.dropout = nn.Dropout(p=drop_prob)

    def forward(self, x):
        x = self.linear1(x)
        x = self.relu(x)
        x = self.dropout(x)
        x = self.linear2(x)
        return x

순서!!
1. linear1(x) 는 입력 x를 은닉층 차원으로 변환.
변환 전 [batch_size, seq_len, d_model] -> 변환 후 [batch_size, seq_len, hidden] self.linear1 = nn.Linear(d_model, hidden)
2. ReLU 활성화 함수를 적용하여 비선형성을 추가한다. 이는 모델이 복잡한 함수를 학습할 수 있도록 도와준다. ReLU 함수는 음수 값을 0으로 변환하고, 양수 값은 그대로 유지
x = self.relu(x)
3. 드롭아웃 레이어를 적용하여 일부 뉴런을 무작위로 비활성화 한다. 이는 과적합 방지와 모델의 일반화 성능을 향상. 드롭아웃은 학습 시에만 적용되며, 추론시에는 모든 뉴런이 활성화 됨.
x = self.dropout(x)
4. linear2(x) 는 은닉층 차원의 데이터를 출력 차원으로 변환한다. 이 변환을 통해 원래 입렵 차원 d_model로 다시 변환 된다.
변환 전 [batch_size, seq_len, hidden] -> 변환 후 [batch_size, seq_len, d_model]

질문!!
Q. ReLU 활성화 함수를 사용해서 왜 비선형성을 추가하는거야?
A. 신경망이 더 복잡한 함수를 학습할 수 있게 하기 위함. 비선형성은 신경망이 단순한 선형 변환 이상의복잡한 표현을 학습하는데 필수적
장점

• 계산이 효율적 -> 학습과 추론 속도를 높임
• 기울기 소실 문제(vanishing gradient problem)완화. 이는 역전파 과정에서 기울기가 사라지는 문제로, 특히 깊은 신경망에서 발생할 수 있다. ReLU는 양수 구간에서 기울기가 1이므로, 역전파 시 기울기가 사라지지 않는다.
• ReLU 는 입력 값이 0 이하일 때 출력을 0으로 만든다. 이는 희소 활성화를 촉진하여 일부 뉴런이 활성화되지 않는 효과를 가지ㅁ, 모델의 효율성과 일반화 능력 향상.