그래프란

정점(노드, Vertex)과 간선(Edge)으로 구성된 자료구조

트리보다 확장된 개념

• 예: SNS 관계, 지하철 노선도 등

---

정점(Vertex)

• 각 노드를 의미
• SNS → 유저, 지하철 → 역

간선(Edge)

• 정점과 정점을 잇는 선
• 방향이 있을 수도 있고 없을 수도 있음
• 간선에 가중치(Weight)가 있을 수도 있음 → 거리, 비용 등

---

방향 그래프 vs 무방향 그래프

• 무방향 그래프: A ↔ B (양방향 이동 가능)
• 방향 그래프: A → B (한 방향만 가능)
• 차수(Degree): 한 정점과 연결된 간선 수
  • 무방향 그래프: 그냥 차수
  • 방향 그래프:
    • 진입차수(In-degree): 들어오는 간선 수
    • 진출차수(Out-degree): 나가는 간선 수

---

사이클(Cycle)

• 출발한 정점으로 다시 돌아올 수 있는 경로가 있는 경우
• 순환이 있음

---

연결 요소 (Connected Component)

• 간선들을 통해 모두 연결되어 있는 정점들의 집합
• 연결 그래프: 모든 정점이 서로 연결됨
• 비연결 그래프: 일부 정점들이 떨어져 있음

그래프 표현 방식

그래프를 표현하는 방식은 인접 행렬 (Adjacency Matrix)와 인접 리스트 (Adjacency List) 2가지가 있다.

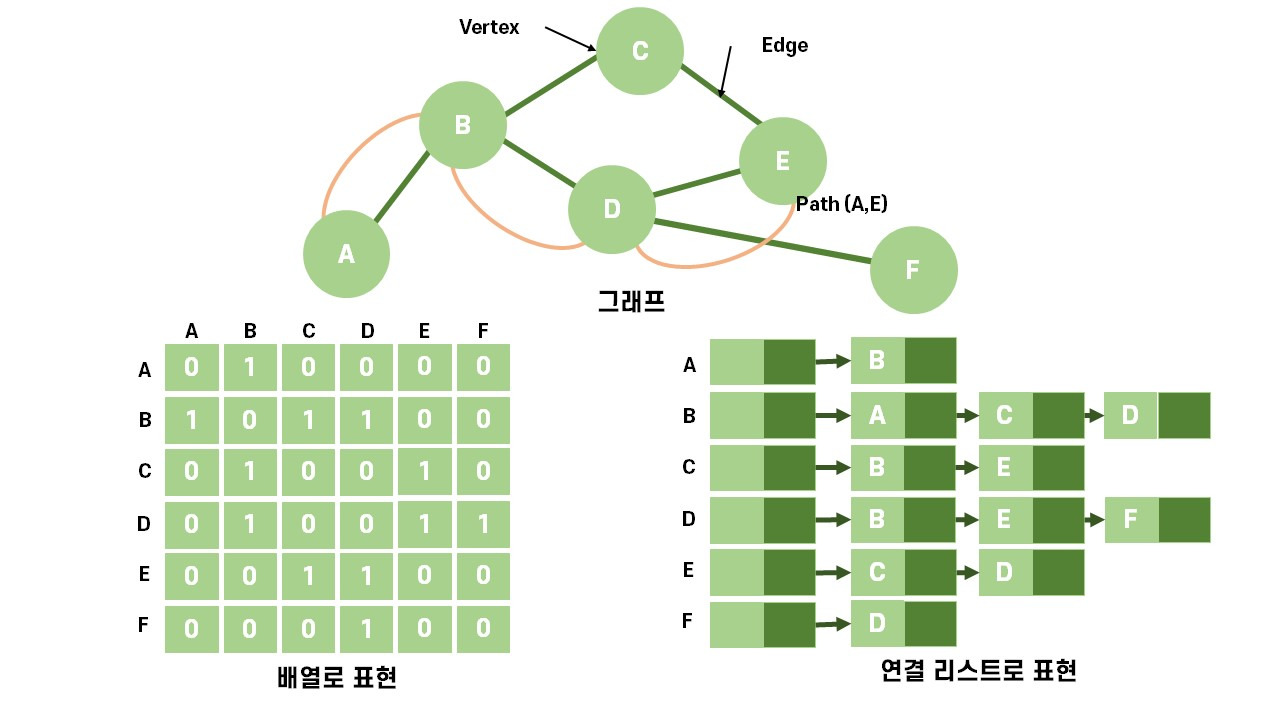
1. 인접 행렬 (Adjacency Matrix)

2차원 배열을 이용하여 정점 간의 연결 여부를 나타냄.

공간 복잡도는 O(V²).

// 정점 수 V = 6 (1번부터 6번까지)
const V = 6;
const graph = Array.from(Array(V + 1), () => Array(V + 1).fill(0));

// 간선 추가 (1 → 5, 1 → 3 등)
graph[1][5] = 1;
graph[1][3] = 1;
graph[3][2] = 1;
graph[3][5] = 1;
graph[4][3] = 1;
graph[4][6] = 1;
graph[6][4] = 1;

// 예시: 1 → 5 연결 여부
console.log(graph[1][5]); // 1 (연결됨)
console.log(graph[1][2]); // 0 (연결 안됨)

2. 인접 리스트 (Adjacency List)

각 정점이 연결된 정점들의 리스트를 갖는 방식.

공간 복잡도는 O(V + E).

const V = 6;
const graph = Array.from(Array(V + 1), () => []);

// 간선 추가
graph[1].push(5, 3);
graph[2] = [];
graph[3].push(2, 5);
graph[4].push(3, 6);
graph[5] = [];
graph[6].push(4);

// 예시: 정점 3에서 연결된 노드 출력
console.log(graph[3]); // [2, 5]

정리 비교표

항목	인접 행렬	인접 리스트
표현 방식	2차원 배열	배열의 배열 (리스트)
공간 복잡도	O(V²)	O(V + E)
간선 확인	O(1)	O(정점의 차수)
연결된 정점 순회	O(V)	O(정점의 차수)
장점	구현이 간단, 연결 여부 빠르게 확인	메모리 절약, 많은 간선에 유리
단점	메모리 낭비 가능	연결 여부 확인이 느림