Automous System

통신을 할 때에는 AS로 나누어진다. AS끼리는 또 묶여 있는 경로가 있다. AS1에서 AS2로 가려면 최단경로가 존재하지만 AS3를 거쳐가는 것이 더 저렴하기 때문에 그것을 Rule로 정해둔다.
Routing Protocol
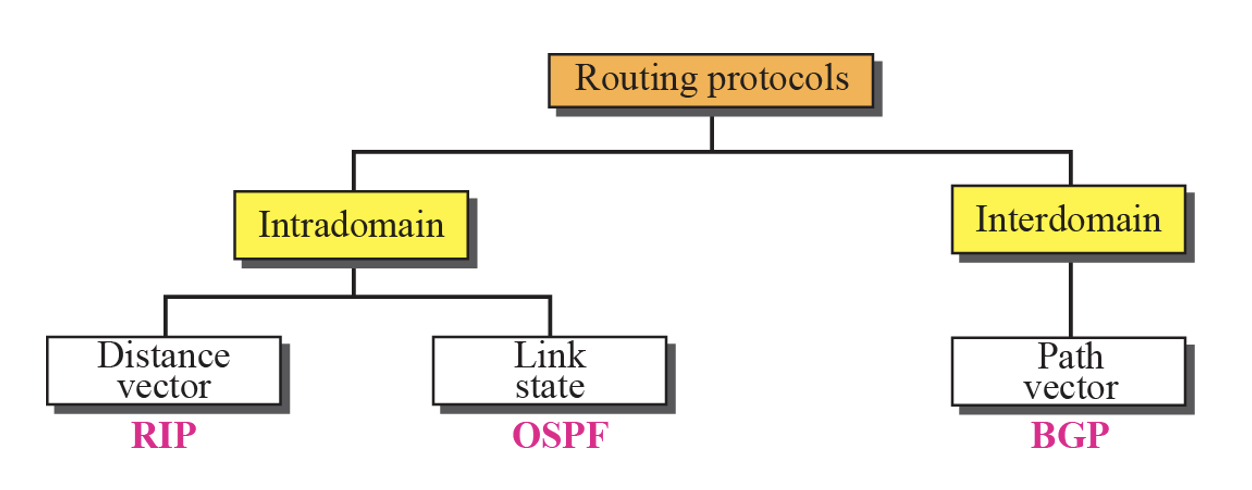
AS끼리는 InterDomain으로 연결이 된다. 그리고 AS안에서 작동하는 것이 IntraDomain이다. RIP는 Distance vector로 만든 프로토콜이다. 이런 식으로 박스 안에 있는 것은 개념을 의미한다.
Distance Vector
Distance Vector은 Bellman-Ford algorithm을 기반으로 만들었다. i에서 j로 최단경로를 구하고자 한다. 이미 경로를 알고있고 구해놨다고 가정을 한다. 비교를 다 해봤더니 2번 path가 가장 짧으면 i-j 최단경로는 2번이다.
최초 테이블

이것은 최초의 테이블이다. 자신의 입장에서 다이렉트하게 연결된 정보만 담겨있다. A입장에서는 E가 어디에 있는지 직접 연결되어 있는지 모르기 때문에 무한대로 표시가 되어있다.
새로운 테이블을 만드는 과정
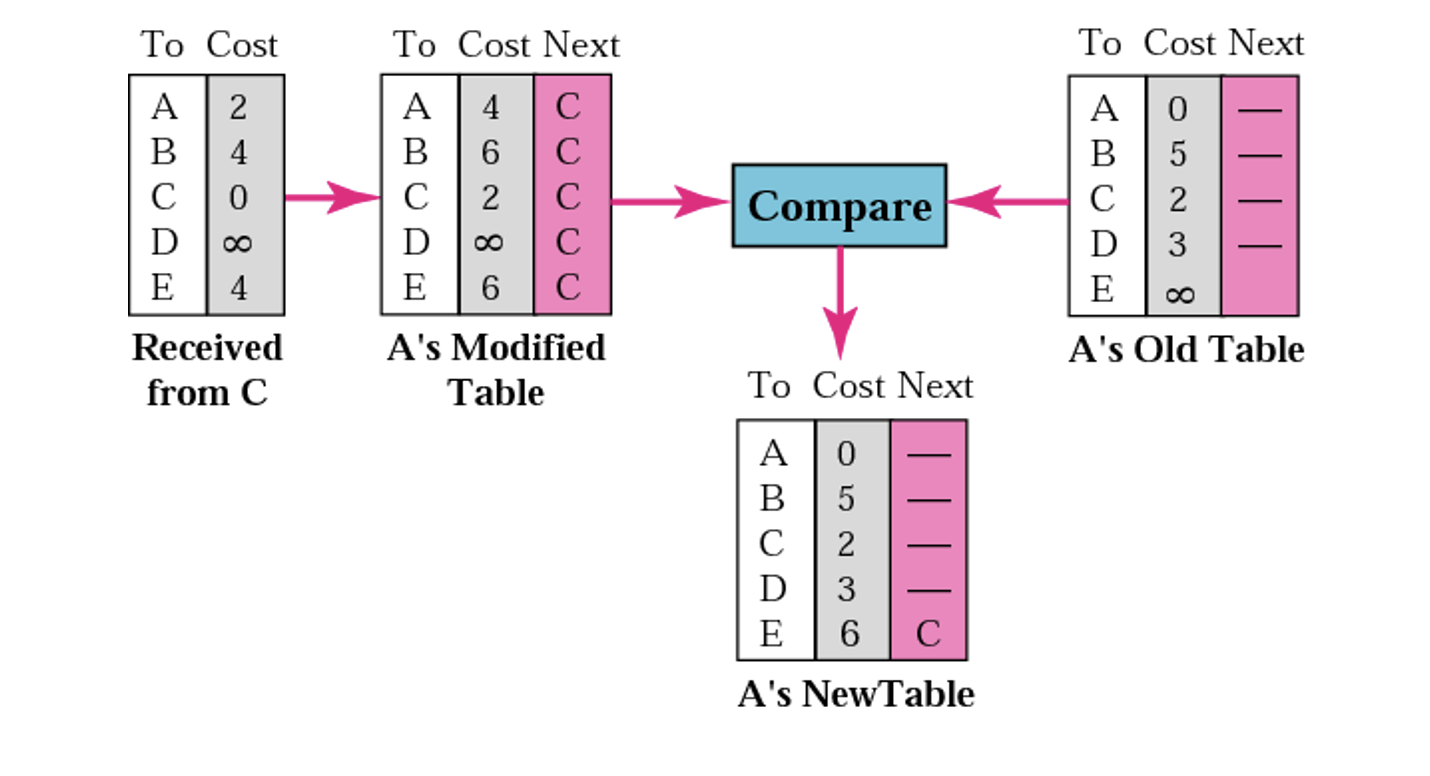
오른쪽에는 우리가 처음 봤던 A의 테이블이 위치한다. 왼쪽에는 A의 테이블을 모두 C로 하고 cost인 2를 모두 더해준다. 그리고 옛날 테이블과 비교를 하는 것이다. 비교를 하면서 상대적으로 더 낮은 값이 있다면 그 값을 cost로 update해준다.
새로운 테이블
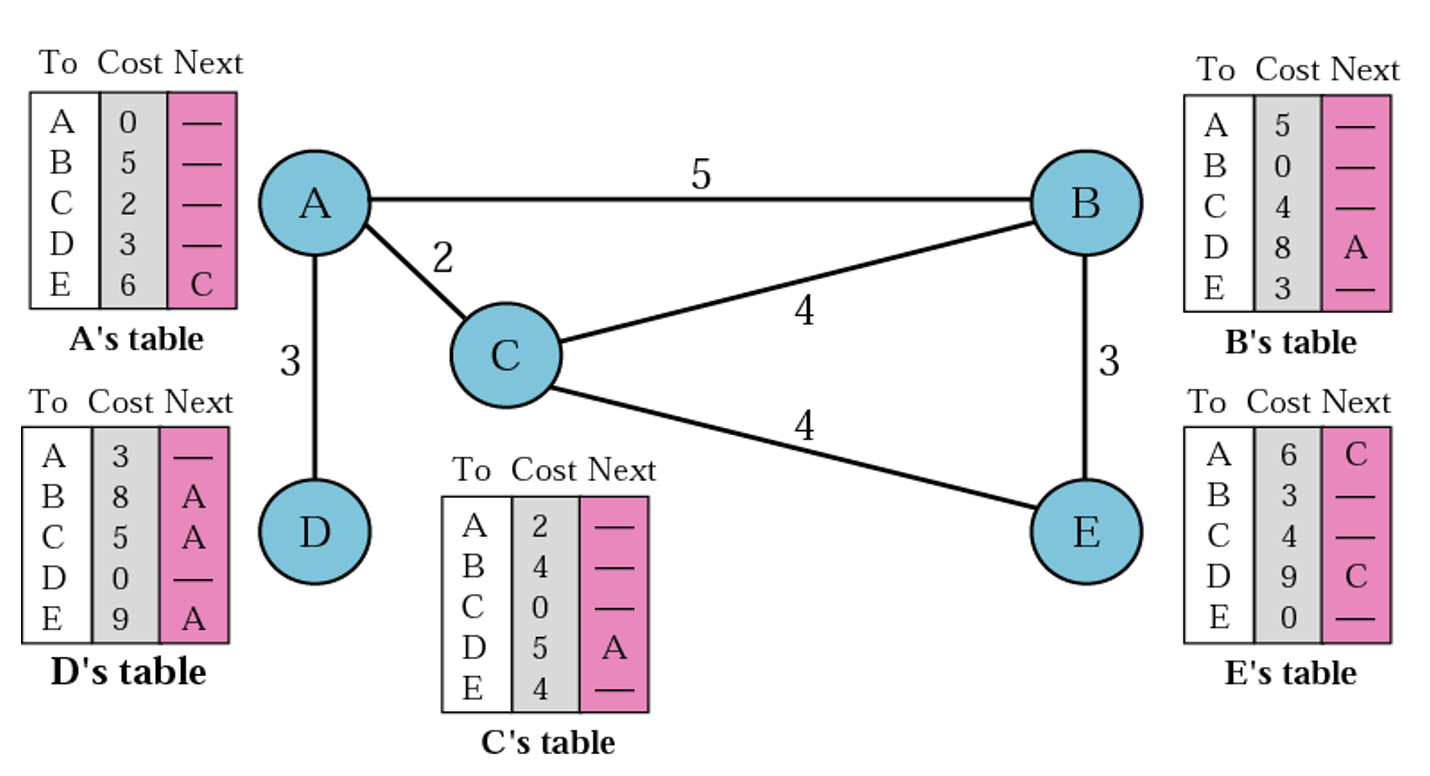
그렇다면 Bellman-Ford algorithm과 마찬가지로 각자의 위치에서 특정 위치로 갈 때 최소 길이가 다 적혀있는 테이블을 만들 수 있다.
Example
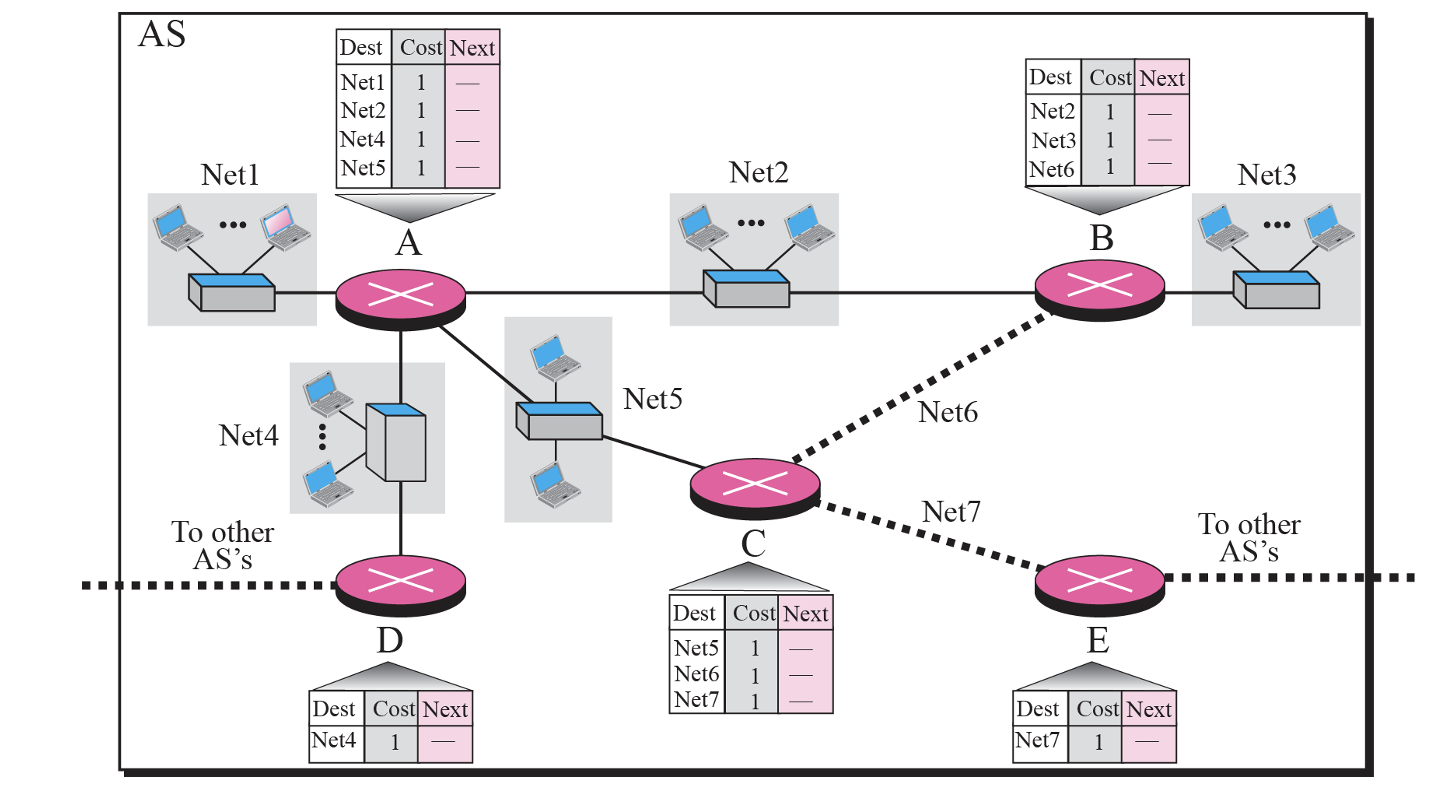
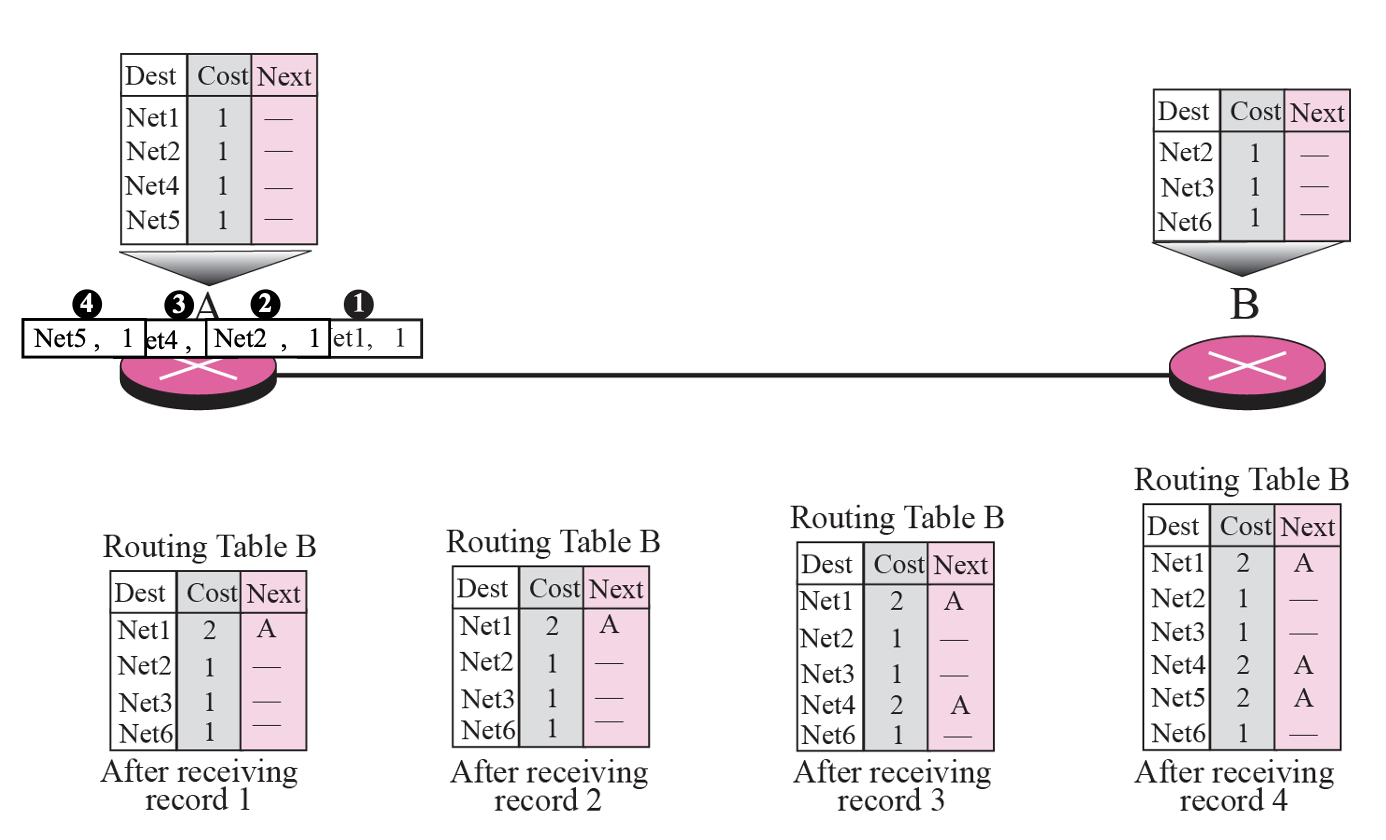
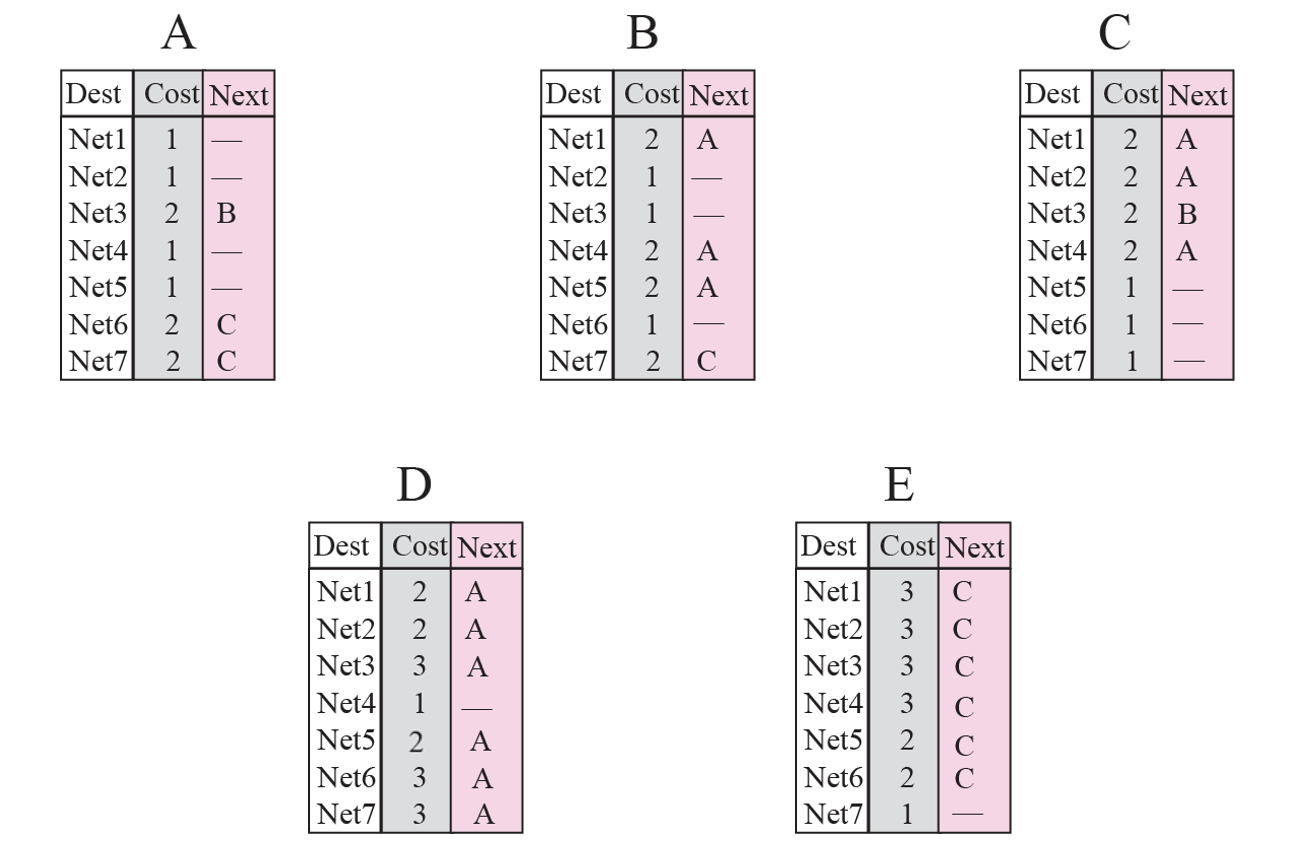
위 테이블을 기준으로 테이블을 만들 것이다. 우선은 모두 default로 1로 설정해둔다. A의 입장에서 먼저 살펴보자. 두번째 그림을 보면 A의 입장에서는 네트워크1, 2, 4, 5가 연결되어 있지만, B는 네트워크2, 3, 6밖에 없다. 네트워크 A와 B가 직접 연결되어 있는 것은 1이 최단거리이기 때문에 업데이트할 필요가 없다. 하지만 A에게만 있는 1, 4, 5는 B에게 없기 때문에 +1씩 해줘야 한다. 이러한 방식으로 모든 네트워크를 업데이트 해주면 된다.
Two Node Instability
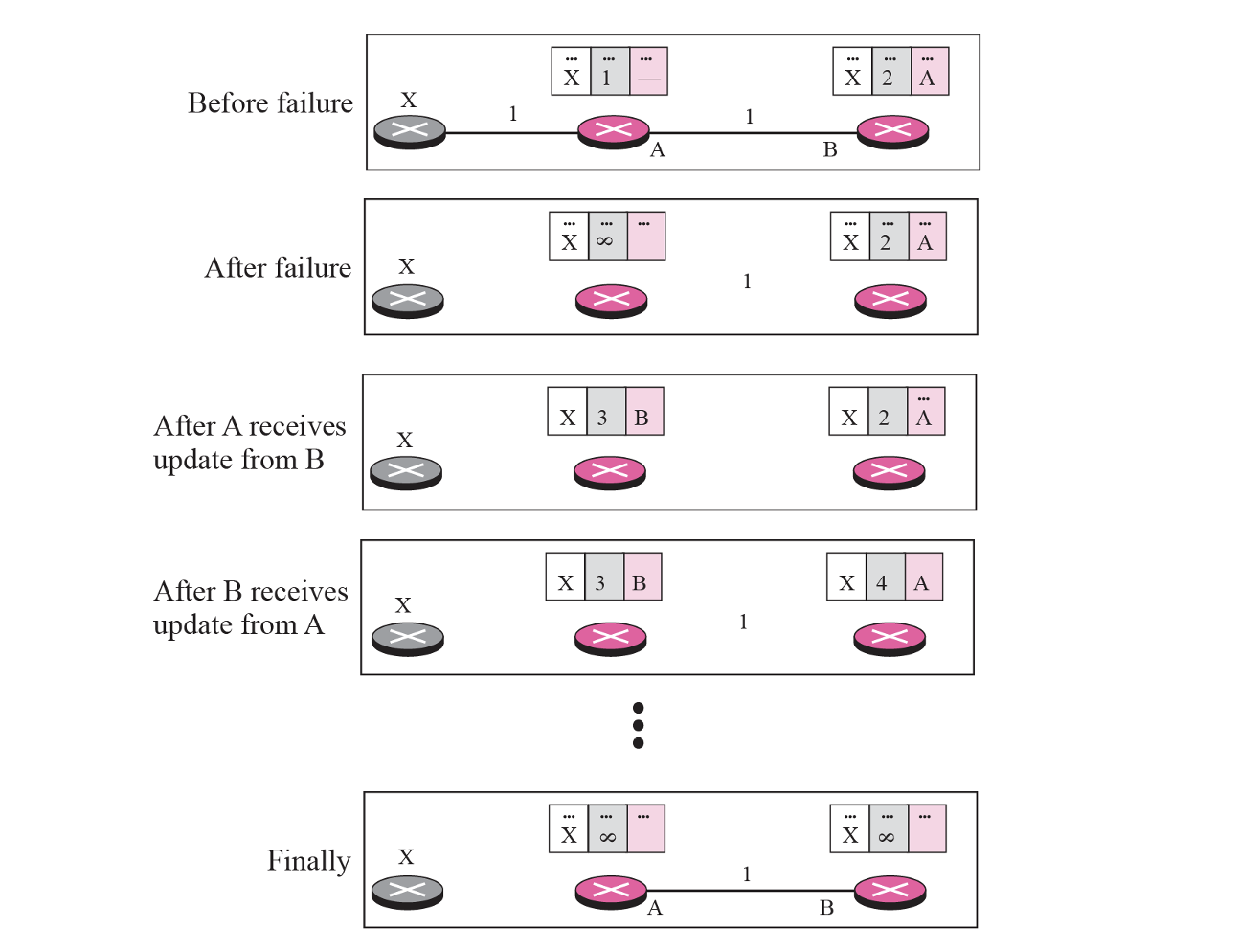
첫번째 칸을 본다면 X로 가려면 A는 cost1만큼 걸리고 넥스트는 없다. B입장에서는 X로 가려면 cost2만큼 걸리고 넥스트는 A이다. A가 B한테 정보를 주면 B는 이 정보로 업데이트를 한다. 하지만 두번째 칸을 보면 A에서 X로 가는 링크가 깨졌다. 라우터끼리는 주기적으로 주고 받는다. 전달이 계속 오지 않는다면 링크가 깨진걸로 간주하고 cost를 무한대로 바뀐다.
이제 이 정보가 B한테 가면 되는데 이 정보를 주고받을 때 2가지 case에 의해서 주고받는다. 하나는 주기적으로 주고받는 것이고, 또는 업데이트가 되면 주고 받는다.
운이 나쁠 경우에는 A가 B에게 정보를 줘야 하는데 그 전에 B가 A한테 먼저 보내는 경우가 있다. 기존에 내가 갖고 있는 것은 무한대였는데 B가 나한테 보내준 걸로 했더니 더 작은 코스 3으로 바뀌고 B로 가면 X까지 갈 수 있다고 착각을 한다. 그래서 A가 가지고 있는 것이랑 비교를 해보고 업데이트를 한다. 넥스트가 똑같으면 새로운 값으로 update를 하고 넥스트가 다르다면 "아 다른 길도 있구나"하고 업데이트를 하는 것이다. 이 주고받는 것을 무한대가 될 때까지 진행한다.
이러한 문제를 해결하기 위한 방법은 세가지가 있다.
무한대는 16으로 set
cost가 16이면 멈춘다. 한 AS안에서 봤을 때 16은 충분한 숫자이다.
Split horizon
B가 A한테 정보를 줘서 위에 문제가 발생하였다. X에 대한 정보를 B입장에서는 A가 제일 잘 알고 있다. 그걸 A에게 다시 안주면 된다. 혼란을 방지하기 위함이다. 그래서 B입장에서는 넥스트가 A인 것은 A한테 주지 않는 것이다. 즉, B가 A한테 보낼 때, 넥스트가 A인 것, 넥스트가 상대방인 경우는 그 라인을 빼고 나머지를 전송한다.
Split horizon & Poison reverse
보내주긴 보내주는데 cost를 무한대로 해서 보내준다. 한마디로 그냥 "A입장에서 참고만 해" 용도이다.
Example
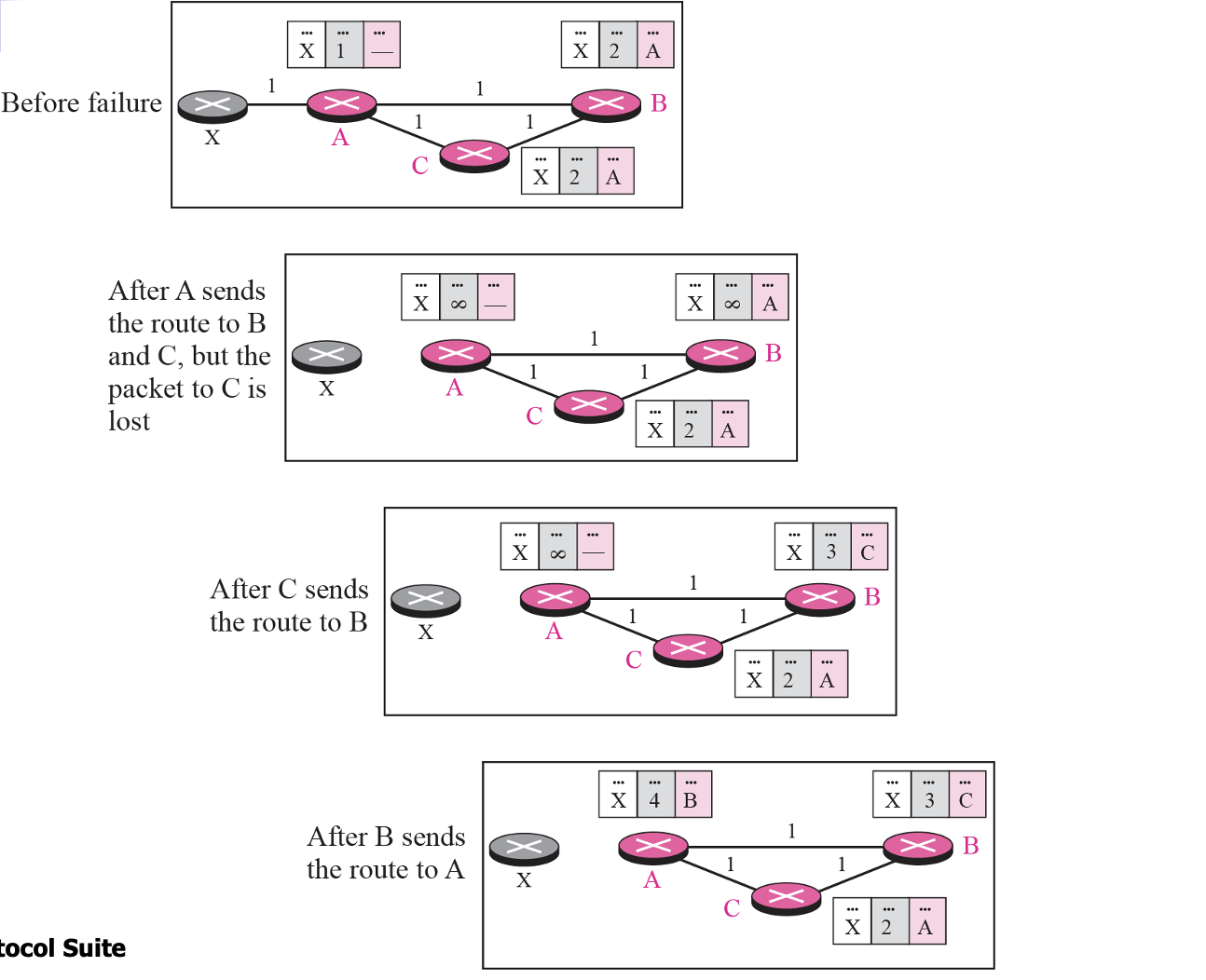
위 그림이 총정리를 한 그림으로 생각하면 된다. 먼저 X에서 A로 가는 연결이 깨졌다. 그렇다면 A는 그것을 알아채고 무한대로 업데이트 해준다. C에서 A로 가는 것도 딱히 문제가 될 것 같지는 않지만 여기서 C -> B로 가는 길이 문제이다. cost가 +1이 되기 때문에 B는 2+1을 한 3이 되고 그렇게 무한루프로 A, C, B가 계속 1씩 증가해버리는 문제가 생긴다.
Link State Routing
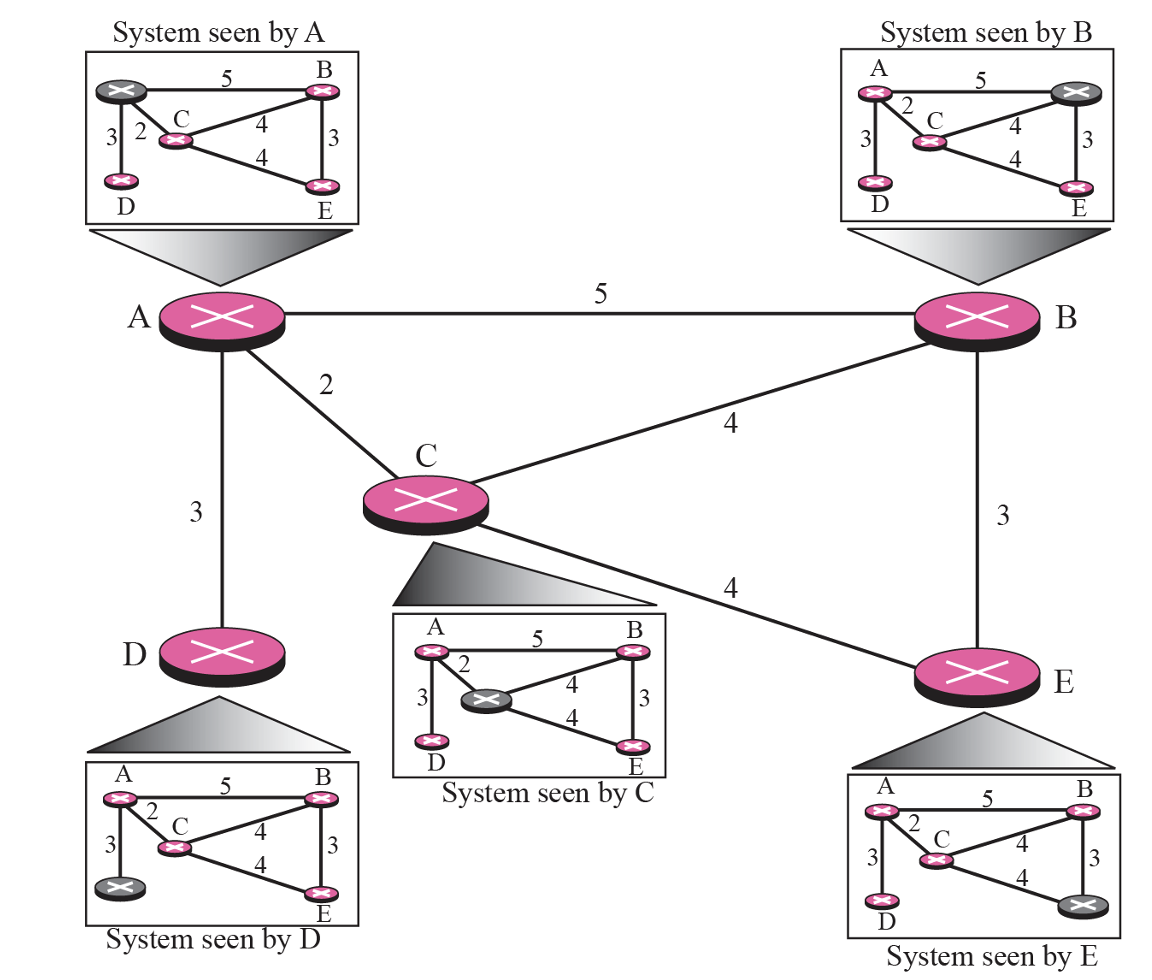
불안정하지만 조금씩 업데이트하는 역할을 Distance Vector에서 했다면 Link State Routing은 A라우터 정보를 다이렉트하게 연결된 라우터 말고 전체한테 뿌린다. 그리고 최단경로를 찾는 방법이다.

다이렉트하게 연결된 link state를 취합하는 것이다.
Dijkstra Algorithm
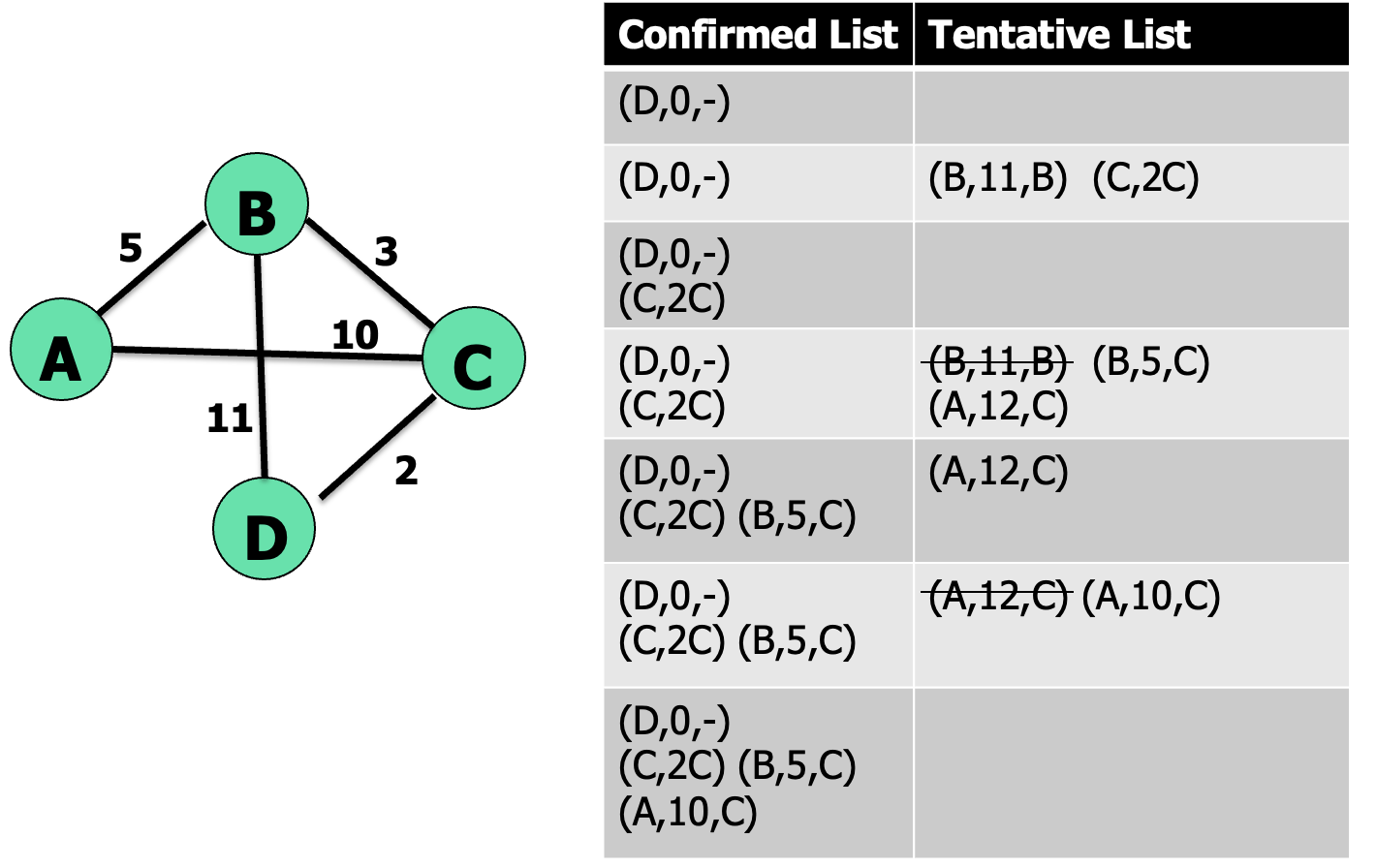
D가 루트를 잡고 최단경로를 찾아가는 방법을 계산할 것이다.
D로 갈 수 있는 것이 B로 11, C로 2가 있다. 이것을 Tentative List에 넣어주고(후보군), 그리고 그 중에서 제일 짧은 것을 Confirmed List로 넣어준다. 후보군에 있는 것은 다음 경로를 계산할 때에도 그대로 넣어준다. 그리고 C에서 갈 수 있는 것을 또 후보 리스트에 넣어준다. 그리고 Confirmed List에 들어있다면 지워준다. A 하나만 남았는데 A 12 C보다는 A 10 C가 더 짧기 때문에 전자를 지우고 후자를 넣어주면 된다. 그리고 Confirmed List에 넣어주면 된다.
Example 1
루트가 A
(A, 0, -)
(A, 0 , -) ⇒ (B, 5, B) (C, 10, C)
(A, 0 , -)
(B, 5, B) ⇒ (C, 8, B) (D, 16, B) (C, 10, C)
(A, 0 , -)
(B, 5, B)
(C, 8, B) ⇒ (C, 8, B) (D, 16, B) (D,10,B)
(A, 0 , -)
(B, 5, B)
(C, 8, B)
(D,10,B)
루트가 B
(B, 0, -)
(B, 0 , -) ⇒ (A, 5, A) (C, 3, C) (D, 11, D)
(B, 0 , -)
(C, 3, C) ⇒ (A, 13, C) (D, 5, C) (A, 5, A) (D, 11, D)
(A, 0 , -)
(B, 5, B)
(A, 5, A) ⇒ (D, 5, C)
(A, 0 , -)
(B, 5, B)
(A, 5, A)
(D,5,C)
Example 2

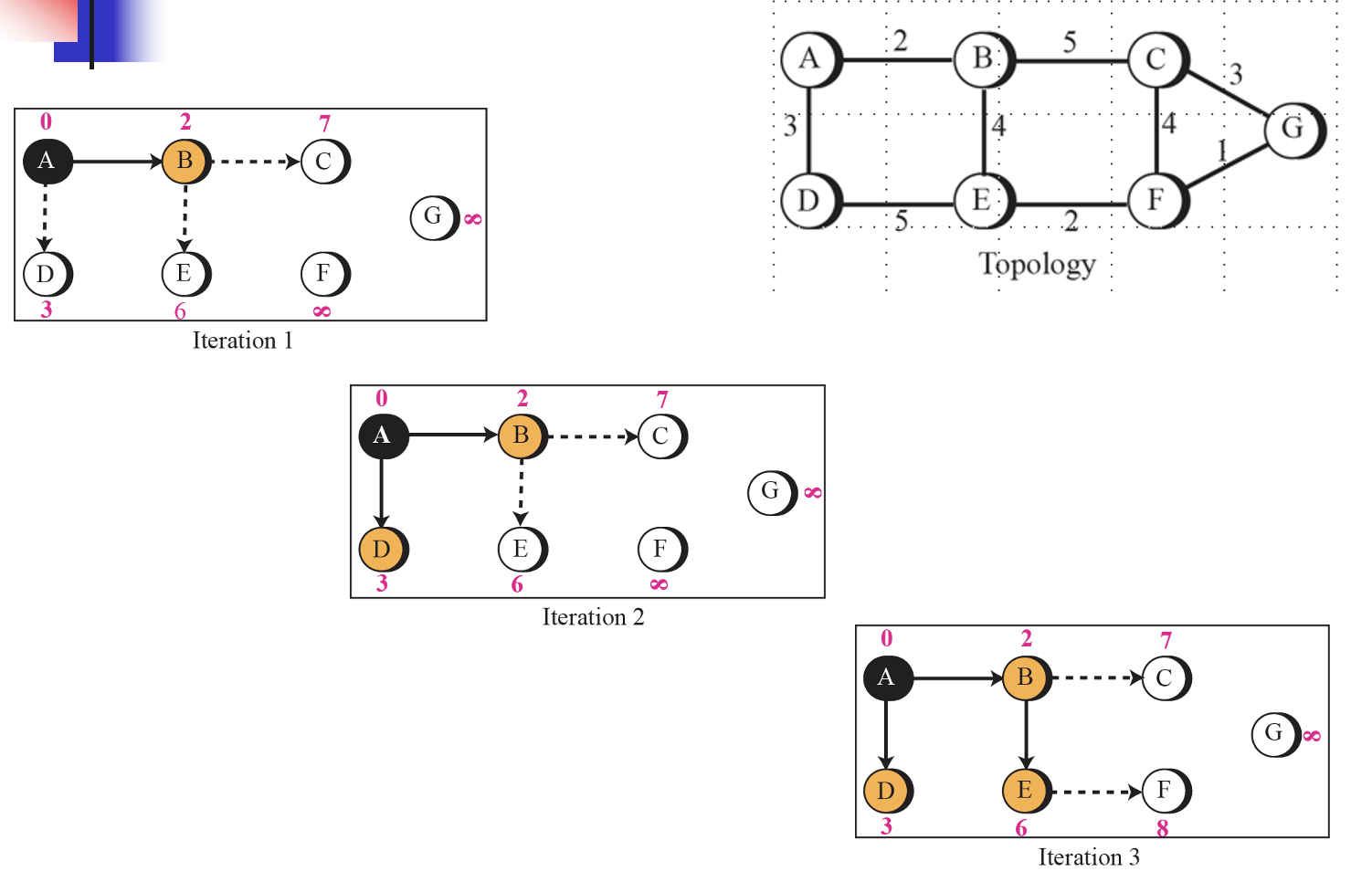
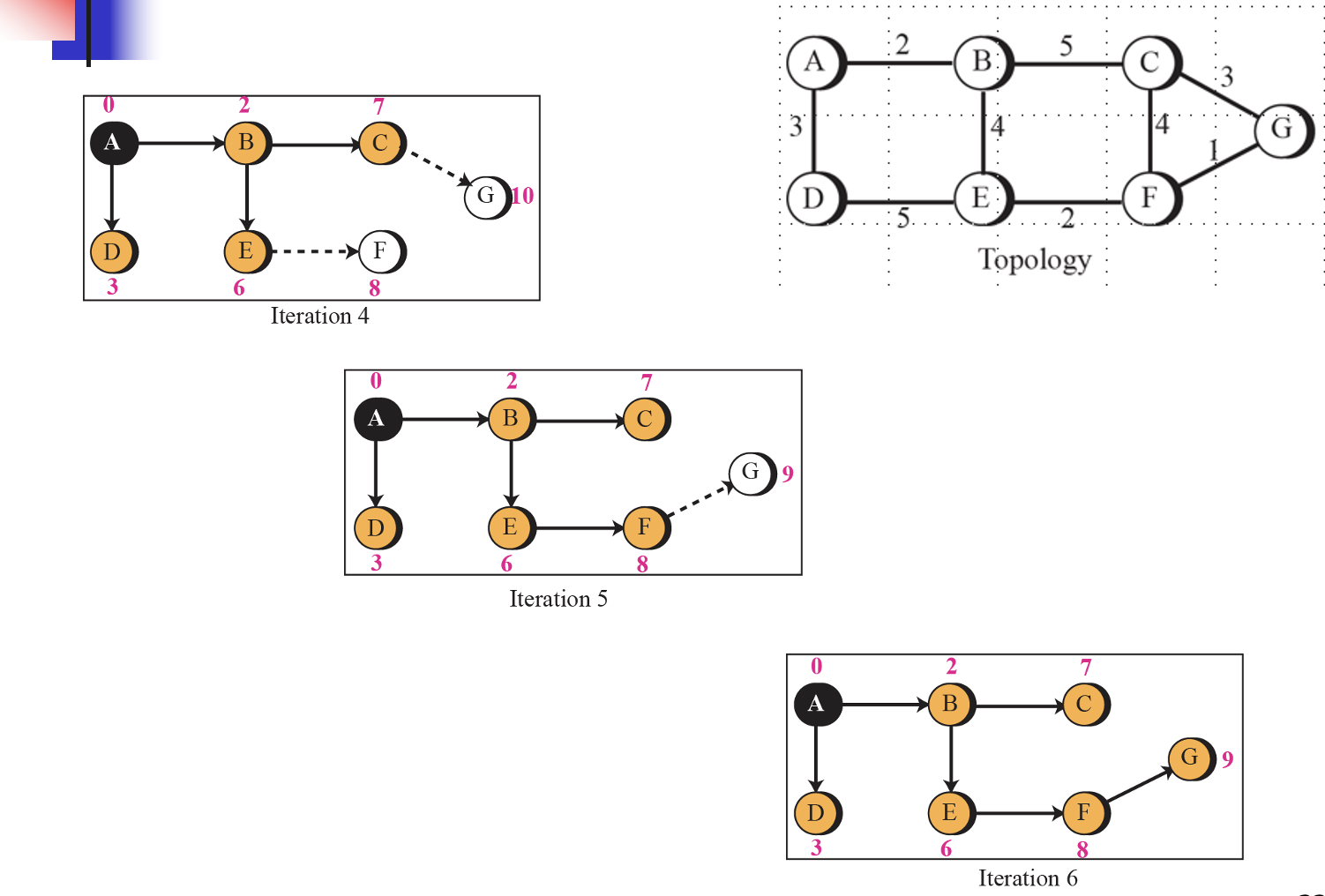
위에 배웠던 다익스트라 알고리즘 방법을 적용하여 루트가 A를 기준으로 적용해보자. 최종적인 노선을 그렸다면 아래와 같이 테이블을 그려주면 된다. 하지만 주의해야할 점은 루트(A)를 기준으로 Next Router을 적어주는 것이다.
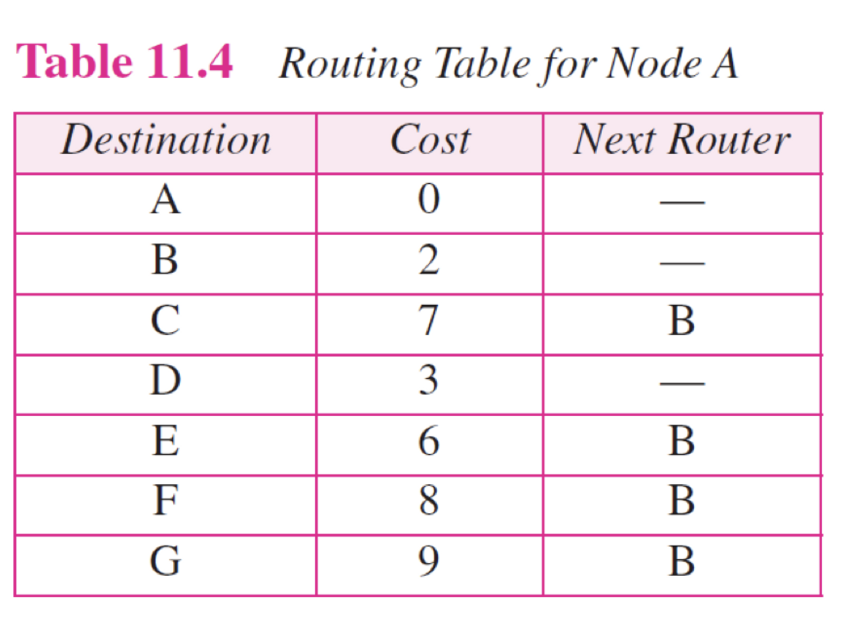
이것은 처음 그림을 최종적으로 테이블로 만든 것이다. 주의해야할 점은 루트를 기준으로 Next Router을 적어주는 것이다.
Example 3

루트가 C인 것을 기준으로 위와 같이 한번 그려보자. 위 그림은 C가 루트인 경우를 그린 것이다. C에서 다이렉트하게 연결 된것을 먼저 찾는다. 최소 cost는 G이므로 G를 확정짓는다. 그리고 G에서 갈 수 있는 것은 둘 다 4이므로 F를 연결한다. 그리고 6하고 5이니까 B를 집어 넣는다. 그리고 6과 9이므로 6을 연결한다. 7과 6중에서 6을 연결한다. 7도 하고, 10하고 11은 10이니까 7을 D와 연결해준다.