소개
컴퓨터 알고리즘 : 문제 해결
문제(problem)를 해결할 때 Input과 Output으로 정의한다. 또한 전략(strategy)을 잘 세워서 문제를 해결해야 한다. 이후에 문제를 해결하기 위한 알고리즘(algorithm)을 잘 정리하면 된다. 그리고 해당 알고리즘을 분석(analysis)한다. 그리고 해당 알고리즘을 구현(implementation)해야 한다. 검증까지 하게 된다면 완료.
알고리즘을 분석할 때 Primitive Operation 을 카운팅하여 일의 양을 측정한다.(자료구조)
Basic Operation 은 가장 기본이 되는 연산이다.
수학적 Background
복잡도를 분석할 때 많이 사용되는 개념(수열의 합, series 는 급수를 의미)
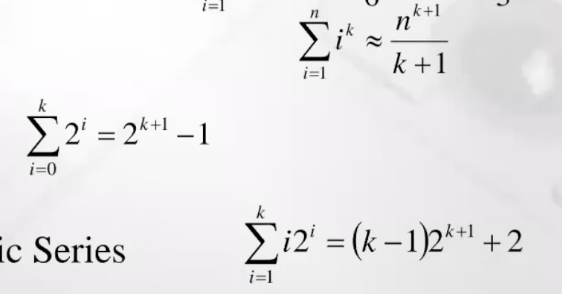
시그마 i=1부터 n까지 i^k 는 n^k+1 / k+1 과 같다.
알고리즘과 문제 분석
_ Correctness
inputs(preconditions) outputs(postconditions)
_ Amount of Work done
일의 양을 따지는 효율성 측정, 기본적인 연산중에서 Basic Operation의 수를 측정해서 n에 대한 함수를 만들면 된다. 대략적으로 파악하기.
일의 양을 측정할 때 input의 properties에 따라서 일의 양이 달라질 수가 있다. →다른 방법에 대해 생각해볼 필요가 있다.
_ Worst-case analysis
수많은 배열 중에서 input size n에 대해서 알고리즘이 수행하는 최대 횟수를 worst case라고 한다. input에 따라 달라질 수가 있다.
⭐️_ Average Complexity
Pr(I)는 input I가 발생할 확률을 의미한다. 이것과 basic operation의 수를 의미하는 t(I)를 곱해서 계산하면 평균 수행시간을 구할 수 있다. Pr(I)는 경험이나 가정을 두고 수행한다. 정확하게 계산할 수는 없다.

A(n)은 탐색에 성공할 때 확률과 실패할 때 확률을 계산해주면 된다.
k가 i번째에서 발생할 확률은 1/n이다. 이것을 가정하고 시작한다.
t(I)는 비교연산의 수를 따져주면 된다. 각 배열을 하나하나 비교. i번째 항에서 발견이 된다고 하면 비교연산은 i+1번 비교가 필요하다. 예를들어 0번째 배열은 1번의 연산, 1번째 배열은 2번의 연산이 필요하기 때문.→성공할 확률 = (n+1)/2
탐색에 실패할 경우는 k가 배열에 존재하지 않는 1가지 케이스밖에 없다. 따라서 시그마가 무의미하다. 실패할 조건부 확률은 1이고 t(I)만 계산하면 n이다.→실패할 확률 = n
A(n) = q (n/2 + 1) + (1-q) n
_ Space Usage and Simplicity
시간을 줄이기 위해서 공간을 많이 차지하게 되는 경우가 발생하기도 하기 때문에 시간과 공간은 Tradeoff 관계이다.
- 알고리즘이 심플하게 작성되면 쉽게 분석할 수 있는 장점이 있다.
- 심플하게 구현이 된다면 유지, 보수 등이 쉬워진다.
_Optimality
문제마다 고유의 complexity가 존재한다. 문제의 complexity는 그 문제를 해결하기 위해 필요한 최소 일의 양을 의미한다.
알고리즘의 클래스(Basic Operation의 타입)을 선택해야 한다. → 해당 Basic Operation을 얼만큼 사용했느냐 일의 양을 counting 해주면 된다.
Optimal은 “The best possible”의 의미를 가지고 있다.→앞으로 개발될 수 있는 알고리즘 중에서 가장 좋은 알고리즘을 찾는다는 의미를 가지고 있다.
우리가 개발한 알고리즘 W(n)이 복잡도 F(n)과 같은 것을 보여주면 된다.
만약 다르다면 더 효율적인 알고리즘이 존재하던가 더 타이트한 문제 복잡도 가 존재할 수 있다.
두개의 행렬(n * n)을 곱하는 문제를 예시로 살펴보자.
이 문제의 basic operation은 ‘곱셈’ or ‘덧셈’이다. 곱셈이라고 가정을 한다면 n^3 time 알고리즘이다.
함수들을 분류하는 방법
- 빅오메가(g): 여기에 속하는 함수들은 g보다 증가율이 크거나 같다. 3n^2 + n + 10, 7n^4도 빅오메가 n^2에 포함되는 함수라고 볼 수 있다.
- 빅오(g): 여기에 속하는 함수들은 g보다 증가율이 작거나 같다.
- 빅세타(g): 여기에 속하는 함수들은 g와 증가율이 같다. 빅세타는 g와 증가율이 같기 때문에
asymptotic order라고도 한다.
- 리틀오(g): 여기에 속하는 함수들은 g보다 증가율이 작다.
- 리틀오메가(g): 여기에 속하는 함수들은 g보다 증가율이 크다.
헷갈리는 경우가 생기면 32p에 나와있는 수식을 이용하면 된다. g(n)을 내가 비교하고자 하는 식을 넣고 상수로 떨어지면 그 값이 맞는거다. 예를 들면 2^(n+1)의 빅세타는 2^n이다.
Transitive: f가 O(g)를 만족하고 g가 O(h)를 만족한다면 f는 O(h)를 만족한다.
Reflexive: f가 빅세타(f)를 만족할 때 → 빅오, 빅세타, 빅오메가도 만족할 수 있다.
Symmetric: f가 빅세타(g)를 만족한다면 g도 빅세타(f)를 만족한다. → 빅세타만 만족한다.
Equivalance: 위 세개를 모두 만족할 때
f가 빅오(g)이면 g는 빅오메가(f)이다.
빅오(f+g) = 빅오(max(f,g))
→ f = 7n^2 + 3, g = 4n^5 + 3n^2 + 100
→ f+g = 4n^5 + 10n^2 + 103
→ 두 함수의 최고차항이 더 큰 함수만 분석하더라도 가능하다.
빅오(1)를 constant라고 한다. 이를 빅오(c) 또는 빅오(0)라고도 한다.
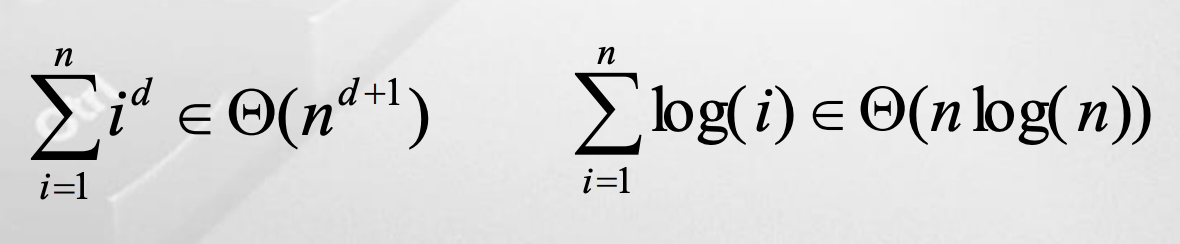
log(i)의 합은 log(1 2 … * n) = log(n!) = nlog(n)
- n! < n^n → n!는 리틀오(n^n)에 속한다.
- n! > 2^n → n!는 리틀오메가(2^n)에 속한다.
- log(n!) = log(n^n) → log n!는 빅세타(logn^n)에 속한다. → 빅세타(n log n)에 속한다.
Ordered Array Searching

Worst Case는 K가 n-1번째 칸에 있을 경우와 K의 값이 n-2번째 보다는 크고 n-1번째보다는 작을 때이다. → 4번에서 n번, 6번에서 1번 총 n+1번 비교하게 된다.

실패할 확률: 배열이 있을 때 각 사이에 있는 값일 때 + 배열 시작 전에 있을 때 + 배열 마지막 칸 이후에 있을 때 = gap이 0부터 ~ n까지 총 n+1개의 경우가 생긴다. gap0은 1번, gap1은 2번, gapi는 i+1번의 연산을 수행하게 된다. 여기서 주의해야 할 점은 gap n일 때 n번 비교연산을 하게 된다. 따라서 gap n-1일 경우 n번 비교연산을 하고 따로 gap n번일 때 비교연산을 합하면 된다. 따라서 총 n+1번 비교한다.
Binary Search
탐색에 성공한 경우는 종료하지만 실패했을 경우에도 인풋의 사이즈를 절반으로 줄일 수 있다는 장점이 있다. 이 알고리즘을 수행할 때에는 다른 알고리즘과 다르게 First와 Last가 주어진다.

재귀함수를 호출하는 형식으로 코드를 짜는데 무한루프에 빠지지 않도록 탈출 조건을 잘 만들어줘야 한다. 주의해야할 점은 1번 라인은 Basic Operation이 아니다. Basic Operation은 K와 엔트리 간 비교를 할 때에만 적용이 된다.
Worst Case는 n 1/2 1/2 … 1/2 = 1 → n (1/2)^k = 1
k = log2n → 빅세타 log2n이다.
Average case
가정: n = 2^d - 1 → 재귀함수를 호출할 때 이런 방식으로 호출이 된다. 꽉 찬 complete binary tree를 가진다.
1번부터 d번까지 시그마 1/n t 2^(t-1)
Sd = 1 1 + 2 2^1 + 3 2^2 + … + d 2^(d-1)
2Sd = + 1 2^1 + 2 2^2 + …+ (d-1) 2^(d-1) + d 2^d
-Sd = 1 + 2^1 + 2^2 + … + 2^(d-1) - 2^d
Sd = (d-1) * 2^d + 1
n = 2^d - 1 → d = log(n+1)
Sd = (log(n+1) - 1)(n+1)+1 = nlog(n+1) + log(n+1) - n -1 + 1
1/n * Sd = log(n+1) + log(n+1)/n -1 = A(success)
A(fail) = 0부터 n까지 시그마 1/(n+1) d = 1/(n+1) d * (n+1) = d = log(n+1)
A(n) = q( log(n+1) + log(n+1)/n -1 ) + (1-q)log(n+1)
Decision Tree
Decision Tree는 Binary Tree이다. input size N과 알고리즘이 생기면 항상 같은 모양의 트리가 완성된다.
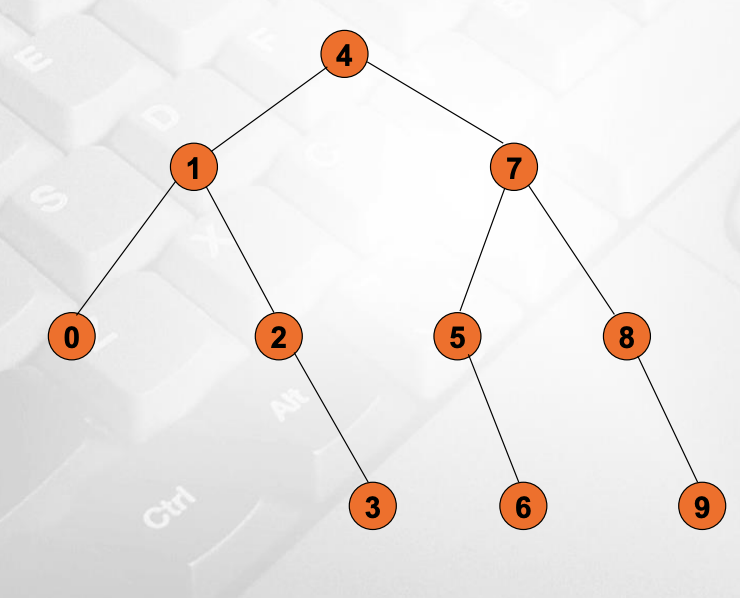
(0+9)/2 = 4.xxx → 루트의 값은 4이다.
(0+3)/2 = 1.xxx → leftChild 값은 1이다.
(5+9)/2 = 7 → rightChild값은 7이다.
.
.
.
이런 방식으로 계속 진행해준다.
알고리즘 A와 B는 순차적으로 검색하기 때문에 input N에 대한 decision tree는 노드의 길이가 n인 풀로 꽉찬 트리 모양이다.
알고리즘 C는 오른쪽 한줄로 쭉 진행되는 노드의 길이가 n인 트리 모양이다.
꽉 찬 트리모양일 때 decision tree의 Worst Case를 계산할 수 있다. 비교연산을 P번 할 때 노드의 수는 1 + 2 + 2^2 + … + 2^(p-1) = N ≤ 2^p - 1 이다.
어떠한 decision tree라도 라지N은 스몰 N보다 크거나 같아야 한다. p ≥ log(n+1)을 만족해야 한다.