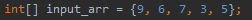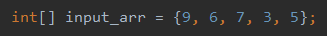알고리즘 성능 분석
프로그램들의 규모가 점차 커짐에 따라 처리하는 데이터의 양이 많아지고 있다. 이러한 경우 프로그램은 많은 데이터를 효율적으로 처리할 수 있어야 한다.
데이터를 처리하는 알고리즘이 입력 데이터 n개를 n^2번 처리하여 결과 값을 출력한다고 가정해보자.
입력 데이터가 100이면 10000번 처리한다.
입력 데이터가 5000이면 25000000번 처리한다.
입력 값은 50배 증가하였으나, 출력 값은 2500배 증가했다. 처리 횟수로만 따지면 24999000번 증가했다.
이러한 경우 알고리즘의 효율성이 떨어진다고 볼 수 있고 이를 개선할 필요성이 있어 보인다.
시간 복잡도
시간 복잡도는 알고리즘이 수행되는데 처리가 몇 번 수행되는지를 나타낸다. 이 시간복잡도를 표현하는 방법은 여러가지가 있지만, 그 중에서도 빅오 표기법을 가장 많이 사용한다.
빅오 표기법은 입력 값이 n개 들어왔을 때 최악의 경우 몇 번 수행되는지를 나타내는 표기법으로 도출되는 n에 대한 수식 중 가장 큰 지수를 가진 항만 남겨 표기한다.
말이 어려울 수 있으니.. 예를 들어보자.
int n = 5;
int sum = 0;
for(int i = 0; i < n; i++){
sum++;
}
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
for(int k = 0; k < 2; k++){
sum++;
}
}
}위의 코드에서 입력값 n은 5로 주어졌다. 맨 처음 단일 반복문에서는 sum++; 연산이 n번 도는 반복문안에 있기 때문에 n번 수행된다.
그리고 삼중 반복문에서는 n만큼 돌며 각 루프마다 n만큼 또 돌고 그 루프안에서 2만큼 또 돈다. 즉 sum++;이라는 연산이 n x n x 2 만큼 수행된다는 것이다.
따라서 n이 5로 주어진 위 알고리즘의 연산 횟수는 5 + 5 x 5 x 2 = 55회이다.
대입연산과 반복문 자체의 비교 연산 등을 제외하고 사칙연산만 놓고 봤을 때, 위 알고리즘의 시간복잡도는 2n^2 + n이라고 볼 수 있다.
빅오 표기법은 이 시간복잡도를 O(n^2)로 표현한다. n의 값에 따라 횟수가 크게 달라지지만 그 앞의 계수와 최고차항을 제외한 항들에 의해서는 횟수가 크게 달라지지 않으므로 가볍게 무시하고 표기하는 것이다.
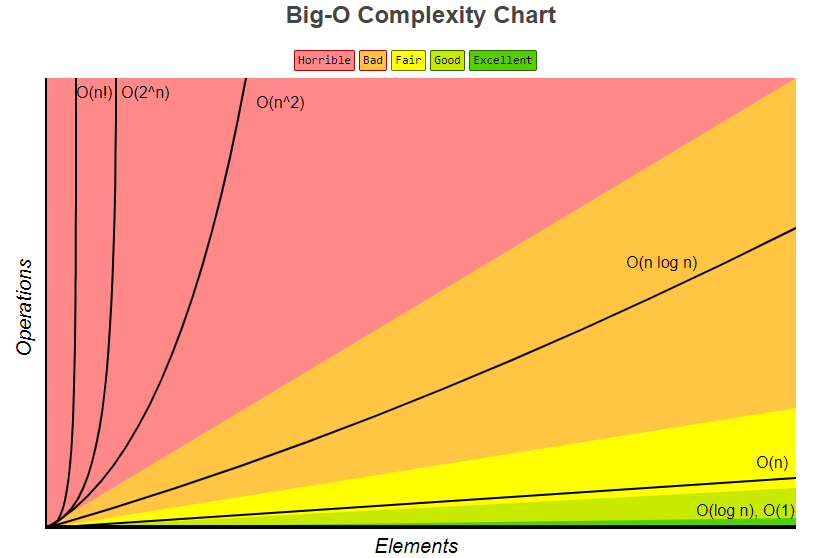
다양한 알고리즘과 시간 복잡도
출처 : https://www.bigocheatsheet.com/
시간복잡도에 따라서 알고리즘의 시간적인 성능을 한눈에 알아볼 수 있다. 아래의 차트는 시간복잡도 별로 연산횟수가 어느정도로 증가하는지를 나타내는 차트이다.
여러 개의 정렬 알고리즘으로 위의 시간복잡도로 알아보는 코드를 구현해보자.
선택 정렬
선택 정렬은 내가 방문하지 않았던 배열에서 최솟값을 찾아서, 현재 위치로 옮기고 다음 위치로 넘어가는 정렬 알고리즘이다.
한 번 반복할 때마다 내 위치에 알맞은 값을 넣어준다고 생각하고 어떤 값을 넣을지에 대해서 전체 배열을 다 반복해서 찾아낸다.
public class SelectionSorting {
public static void main(String[] args) {
// element의 갯수가 input인 것으로 생각한다.
int[] input_arr = {9, 6, 7, 3, 5};
int cnt = selectionSorting(input_arr);
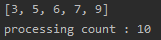
System.out.println(Arrays.toString(input_arr));
System.out.println("processing count : " + cnt);
}
private static int selectionSorting(int[] input_arr){
int cnt = 0;
// i자리에 값을 가지고 비교한다.
for(int i = 0; i < input_arr.length; i++){
// 최솟값은 i자리의 값으로 초기화해둔다.
int minVal = input_arr[i];
int minIdx = i;
// i자리 이후의 값들과 비교하여 더 작은 값이 있으면 갱신한다.
for(int j = i + 1; j < input_arr.length; j++){
cnt++;
if(minVal > input_arr[j]) {
minVal = input_arr[j];
minIdx = j;
}
}
// i자리 이후의 값 중 가장 작은 값을 찾았으니 i자리와 바꿔준다.
int temp = input_arr[i];
input_arr[i] = input_arr[minIdx];
input_arr[minIdx] = temp;
}
return cnt;
}
}코드만 봤을 때 두 개의 반복문으로 시간 복잡도가 O(n^2)인 것을 알 수 있다.
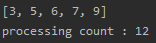
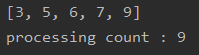
첫 번째 케이스는 비교 횟수가 4, 3, 2, 1 이여서 총 비교 카운트가 10이 출력되었다. 두 번째 케이스는 비교 횟수가 13, 12, ..., 2, 1이여서 총 비교 카운트가 91이 출력되었다.
시간복잡도를 O(n^2)로 표현했지만 연산 횟수가 정확히 5의 제곱인 25, 14의 제곱인 196이 나오진 않았다. 하지만 입력 값이 증가함에 따라 출력 값이 증가하는 추이가 5->14에 따라 10->91인 것은 25->196와 증가 추이가 비슷한 것을 확인할 수 있다.
버블 정렬
버블 정렬은 인접한 두 원소를 비교하여 큰 원소를 뒤로 밀어내는 정렬 알고리즘이다. 1회전 마다 제일 뒤의 인덱스에 정렬되지 않은 배열의 최대값이 쌓여 정렬되어 나간다.
public class BubbleSorting {
public static void main(String[] args) {
int[] input_arr = {9, 6, 7, 3, 5, 4, 10, 14, 1, 2, 0, 12, 1111};
int cnt = bubbleSorting(input_arr);
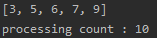
System.out.println(Arrays.toString(input_arr));
System.out.println("processing count : " + cnt);
}
private static int bubbleSorting(int[] input_arr){
int cnt = 0;
// i는 1회전마다 어디 배열까지 돌아갈지 결정한다.
for(int i = input_arr.length - 1; i > 0; i--){
// j는 몇 번째 원소를 비교할 지를 내타낸다.
for(int j = 0; j < i; j++){
cnt++;
// 고른 원소와 그 다음 원소를 비교한다.
if(input_arr[j] > input_arr[j + 1]) {
int temp = input_arr[j];
input_arr[j] = input_arr[j + 1];
input_arr[j + 1] = temp;
}
}
}
return cnt;
}
}
버블 정렬은 항상 반복문의 반복 횟수가 일정하다. 1회전마다 배열의 마지막 자리에 정렬되며 그 다음 회전은 그 앞까지 반복한다.
따라서 n-1, n-2, n-3, ..., 2, 1 번 반복하여.. n(n-1)/2의 시간 복잡도를 가진다. 이는 빅오 표기법으로는 O(n^2)이다.
삽입 정렬
삽입 정렬은 배열들을 미리 정렬해 나가면서, 정렬된 배열들의 중간에 다음 값을 끼워 넣는 식으로 구현되는 정렬 알고리즘이다.
한 번 반복할 때마다 내 앞의 배열 중 나보다 작은 값 다음에 나를 삽입하는 식으로 구현한다.
public class InsertionSorting {
public static void main(String[] args) {
// element의 갯수가 input인 것으로 생각한다.
int[] input_arr = {8, 5, 6, 2, 4};
int cnt = insertionSorting(input_arr);
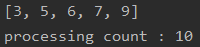
System.out.println(Arrays.toString(input_arr));
System.out.println("processing count : " + cnt);
}
private static int insertionSorting(int[] input_arr){
int cnt = 0;
// 앞에 자리들이랑 비교할 i자리
for(int i = 1; i < input_arr.length; i++){
// 이미 정렬된 앞의 자리들 중 i자리 보다 작은 애가 나오기 전까지 자리를 바꿔간다.
for(int j = i - 1; j >= 0; j--){
cnt++;
if(input_arr[j] < input_arr[j + 1]) break;
int temp = input_arr[j];
input_arr[j] = input_arr[j + 1];
input_arr[j + 1] = temp;
}
}
return cnt;
}
}
삽입 정렬 역시 두 개의 반복문으로 구현되니 시간 복잡도는 O(n^2)이다. 하지만 배열을 정렬하며 처리를 수행하다보니, 이미 어느 정도 정렬되어 있는 경우에는 성능이 좋아질 수 있다. 두 번째 케이스의 경우에는 선택 정렬과 같은 크기의 입력 값(14개)을 주었으나, 이미 어느 정도 정렬된 값을 처리 횟수가 39번으로 두 배 가까이 좋은 성능으로 알고리즘이 수행되었다.
합볍 정렬
합병 정렬은 대표적인 분할 정복 알고리즘 중 하나이다. 전체 배열을 절반으로 나누고 계속 절반으로 나누어 원소의 갯수가 1개가 되었을 때 두 개의 배열을 정렬하며 하나로 합친다.
이 때 devide & conquer 메소드를 사용하며 conquer 메소드에서 두 배열의 인덱스를 비교해가면 정렬된 배열을 합병해낸다.
public class MergeSorting {
public static void main(String[] args) {
int[] input_arr = {9, 6, 7, 3, 5, 4, 10, 14, 1, 2, 0, 12, 1111};
int[] sorted_arr = new int[input_arr.length];
int cnt = mergeSorting(input_arr, sorted_arr);
System.out.println(Arrays.toString(input_arr));
System.out.println("processing count : " + cnt);
}
private static int mergeSorting(int[] input_arr, int[] sorted_arr){ return divide(input_arr, 0, input_arr.length - 1, sorted_arr); }
private static int divide(int[] input_arr, int left, int right, int[] sorted_arr){
int cnt = 0;
int mid = (left + right) / 2;
if(left >= right) return cnt;
cnt += divide(input_arr, left, mid, sorted_arr);
cnt += divide(input_arr, mid + 1, right, sorted_arr);
cnt += conquer(input_arr, left, mid, right, sorted_arr);
return cnt;
}
private static int conquer(int[] input_arr, int left, int mid, int right, int[] sorted_arr){
int cnt = 0;
// 두 분할 배열의 원소의 크기를 비교할 인덱스
int i = left;
int j = mid + 1;
// sorted_arr에 정렬되어갈 인덱스
int k = left;
// i와 j를 비교하며 더 작은걸 sorted_arr에 차례대로 넣는다.
while(i <= mid && j <= right){
cnt++;
if(input_arr[i] <= input_arr[j]) sorted_arr[k++] = input_arr[i++];
else sorted_arr[k++] = input_arr[j++];
}
// 만약 앞의 분할 배열이 남아있다면
if(i <= mid) {
for(int l = i; l <= mid; l++) {
cnt++;
sorted_arr[k++] = input_arr[l];
}
}
// 만약 뒤의 분할 배열이 남아있다면
if(j <= right) {
for(int l = j; l <= right; l++){
cnt++;
sorted_arr[k++] = input_arr[l];
}
}
// 정렬된 분할 배열을 원래 배열에 넣는다.
for(int l = left; l <= right; l++){
input_arr[l] = sorted_arr[l];
}
return cnt;
}
}퀵 정렬
퀵 정렬은 합병 정렬과 비슷하게 두 개의 배열로 나누어 분할 정복하는 알고리즘이다. 하지만 절반으로 나누어 가던 합병 정렬과는 달리 하나의 값을 기준으로 양옆으로 크고 작음을 정렬하여 비정형적인 크기로 분할해나간다.
public class QuickSorting {
public static void main(String[] args) {
int[] input_arr = {9, 6, 7, 3, 5, 4, 10, 14, 1, 2, 0, 12, 1111};
int cnt = quickSorting(input_arr);
System.out.println(Arrays.toString(input_arr));
System.out.println("processing count : " + cnt);
}
private static int quickSorting(int[] input_arr){ return divide(input_arr, 0, input_arr.length - 1); }
private static int divide(int[] input_arr, int left, int right){
if(left - right == 0 || left > right) return 0;
int cnt = 0;
int pivot = input_arr[left];
int low = left + 1;
int high = right;
// low와 high가 바뀌는 순간까지 정렬하면서 내려온다.
while(low <= high) {
if(input_arr[low] > pivot && input_arr[high] < pivot) {
int temp = input_arr[low];
input_arr[low++] = input_arr[high];
input_arr[high--] = temp;
}
if(input_arr[low] < pivot) low++;
if(input_arr[high] > pivot) high--;
cnt++;
}
// 정렬 다하고 피벗을 사이에 끼운다.
input_arr[left] = input_arr[high];
input_arr[high] = pivot;
cnt++;
cnt += divide(input_arr, left, high - 1);
cnt += divide(input_arr, low, right);
return cnt;
}
}
합병 정렬과 퀵 정렬은 n개의 입력이 주어졌을 때 이를 나누어 간다. 합병 정렬을 예를 들어 5개의 입력이 주어지면 1회전에 3, 2개로 나눈다. 그 다음 회전에 2, 1, 1, 1로 나눈다. 그 다음 회전에 1, 1, 1, 1, 1로 나눈다. 즉, log2(n)만큼 반복했을 때 1개짜리 배열로 모두 만들 수 있다.
log2(n)번으로 나누어 분할할 때 각 분할 마다 다시 합병해야하는 원소의 갯수는 n개이다. 따라서 합병 정렬은 O(nlogn)의 시간복잡도를 가진다. 퀵 정렬도 마찬가지이다.