2장은 주로 Confidentiality(기밀성)
3장은 주로 인증 & 서명 (무결성)
✏️ 메시지 인증 방법
- Source Authentication: 메시지의 송신자를 확인하는 것
- Message Authentication: 수신한 메시지가 진짜임을 확인하고, 메시지의 내용이 변경되지 않았음을 검증하는 것
■ 대칭 암호를 이용한 인증
메시지를 반드시 암호화하여 송수신자 간의 인증을 수행한다.
- 송수신자가 동일한 키를 소유
- 오류 감지 코드 사용 (메시지 변경 여부 확인 가능)
- 순서 번호를 사용하여 메시지 순서 변경 탐지 가능
- 타임스탬프를 통해 메시지 지연 여부 확인 가능
■ 암호화 없는 인증
메시지를 암호화하지 않고 인증할 경우, 기밀성은 보장되지 않는다.
- 인증 꼬리표(MAC)를 메시지에 첨부하여 전송
- 메시지 자체는 암호화하지 않음
응용 사례
- 브로드캐스팅: 네트워크 경고 등 메시지를 다수에게 전송할 때
- 메시지 복호화 시간이 부족할 때
- 컴퓨터 프로그램은 평문 상태에서 인증하는 것이 편리할 때
메시지 암호화를 하지 않고 인증하는 방법은 MAC과 해시를 사용한 인증 2가지가 존재한다.
► 메시지 인증 코드 (MAC)
MAC(Message Authentication Code)는 송신자가 비밀키를 이용해 메시지에 작은 데이터 블록을 추가하는 방식이다.
MAC = F(Key, Message)
- 여기서
Key는 송수신자가 공유하는 비밀키이다.- MAC의 크기는 메시지 크기보다 작다.
- 수신자는 수신한 메시지에 키를 적용하여 새로운 MAC을 생성하고, 수신한 MAC과 비교하여 메시지의 무결성을 검증한다.
- 예를 들어, DES를 사용하여 암호문 끝부분의 일부 비트를 MAC으로 사용할 수 있다.
► 해시를 사용한 인증
해시 함수 자체는 비밀키를 사용하지 않기 때문에, 사실상 인증이라기보다는 데이터의 무결성을 보장하는 방법에 가깝다.
1. 블록 암호 사용 방법
- 메시지 다이제스트(Hash(M))를 암호화하여 인증한다.
- 메시지 전체를 암호화하지 않으므로 오버헤드가 줄어든다.
- 공개키 암호 사용 방법
- 메시지 다이제스트를 개인키로 암호화하고, 공개키로 복호화하여 인증한다.
- Nonce(비밀값) 사용 방법
- 송수신자가 공통의 비밀값(S)을 갖고 있으며,
MD = H(S||M)형태로 사용한다.- 여기서
||는 Concatenation(연결)을 의미한다.
암호화 없는 메시지 인증의 이유
- 암호 소프트웨어는 속도가 느리다.
- 암호 장비는 대용량 데이터 처리에 최적화되어 있으나, 작은 데이터 처리 시 오버헤드가 크다.
- 암호 알고리즘에 대한 수출 제약이 존재한다.
✏️ 안전 해시 함수
해시 함수는 메시지 인증과 디지털 서명에 사용된다.
■ 해시 함수의 요건
- 임의 크기의 데이터 블록을 입력으로 받아야 한다.
- 일정한 길이의 출력을 제공해야 한다.
- 계산 용이성과 구현 가능성이 있어야 한다.
- 일방향 성질이 있어야 한다.
- 약한 충돌 저항성: 주어진 x에 대해
H(x) = H(y)를 만족하는 y를 찾기 어려워야 한다. - 강한 충돌 저항성:
H(x) = H(y)를 만족하는 두 개의 서로 다른 입력 쌍(x, y)을 찾기 어려워야 한다.
일방향 성질 (Preimage Resistance)
: 어떤 해시 값
h에 대해H(x) = h를 만족하는 x를 찾는 것이 계산적으로 불가능
H가 일방향이 아니라면?
- 공격자는 메시지와 해시코드 값을 얻게 됨
C = H(S||M)- 공격자는 해시 함수의 역을 게산 ->
S||M을 구함- 공격자는 M과 S(Nonce)를 알 수 있게 됨
약한 충돌 저항성
주어진 블록
x에 대해서,H(x) = H(y)를 만족하는y를 찾는 것이 불가능
약한 충돌 저항성이 성립되지 않으면?
1. 메시지와 암호화된 해시코드 가로채기
2. 메시지로부터 암호화되지 않은 해시코드 생성
3. 동일한 해시코드를 갖는 변조된 메시지를 생성
즉, 위조가 가능해진다.
➜ 무결성 성립 못함
강한 충돌 저항성
생일 공격(Birthday attck)을 방어할 수 있다.
■ 해시 함수에 대한 공격
전수 공격 (Brute Force)
- 해시코드 길이가
n비트일 때:- 일방향 성질 저항성:
2^n의 난이도 - 약한 충돌 저항성:
2^n의 난이도 - 강한 충돌 저항성:
2^(n/2)의 난이도
- 일방향 성질 저항성:
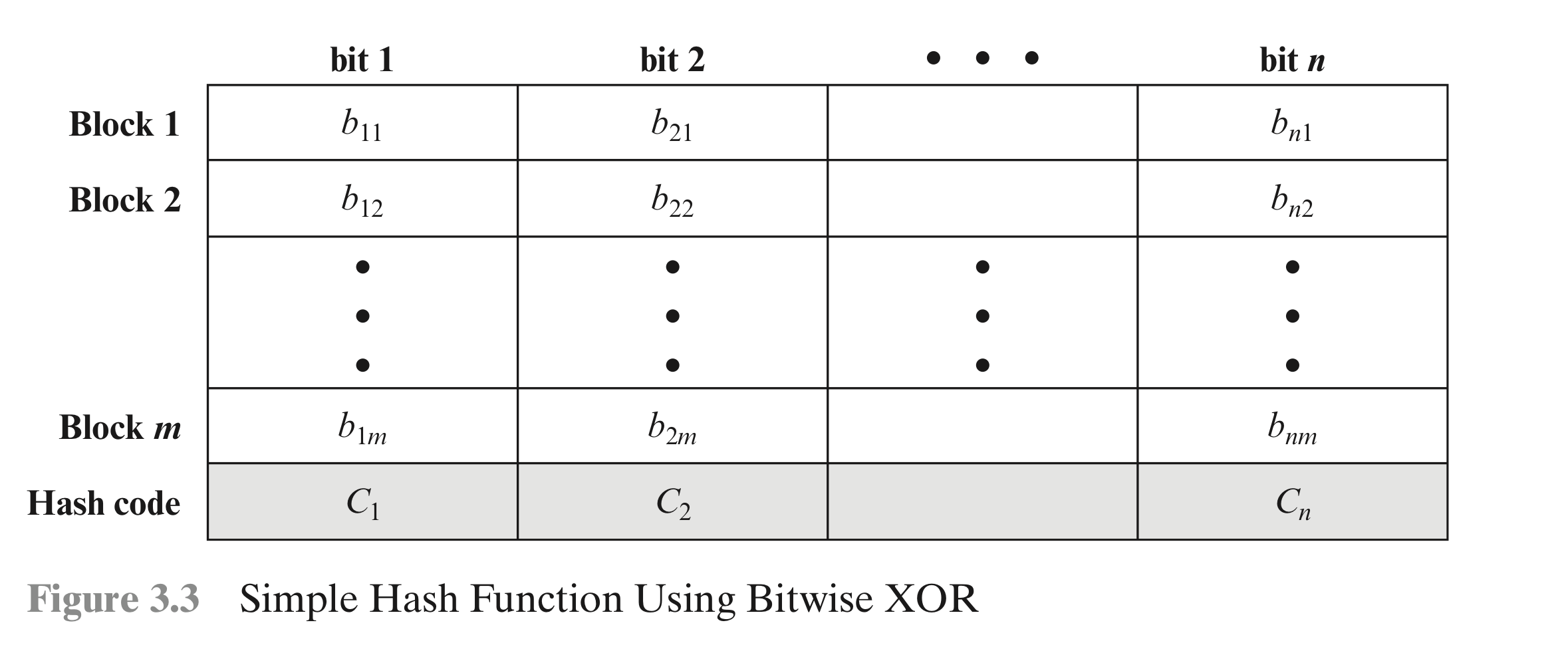
■ 단순 해시 함수
Parity 값을 해시 코드로 사용하는 단순한 방법
충돌 저항성이 없다는 문제가 있다!
➜ 동일한 해시 값을 갖는 다른 메시지를 찾을 수 있다.
b1과 b2를 바꿔도 상관 없다.
Rotated XOR
위의 문제를 해결하기 위해 Rotated XOR방식을 사용한다.
n 비트 해시값을 0으로 초기화 한다.
뒤에 이어지는 n 비트 데이터 블록에 다음과 같은 절차를 시행한다.
- 현재 해시값을 왼쪽으로 한 비트 회전한다.
- 블록을 해시값에 XOR한다.
취약성: 평문 메시지에 해시코드만 암호화하는 경우 단순 XOR, RXOR 모두 취약
공격자가 평문 메시지로부터 동일한 해시 코드를 생성하는 다른 메시지를 찾는 것이 용이함
■ SHA
SHA는 안전 해시 함수이다.
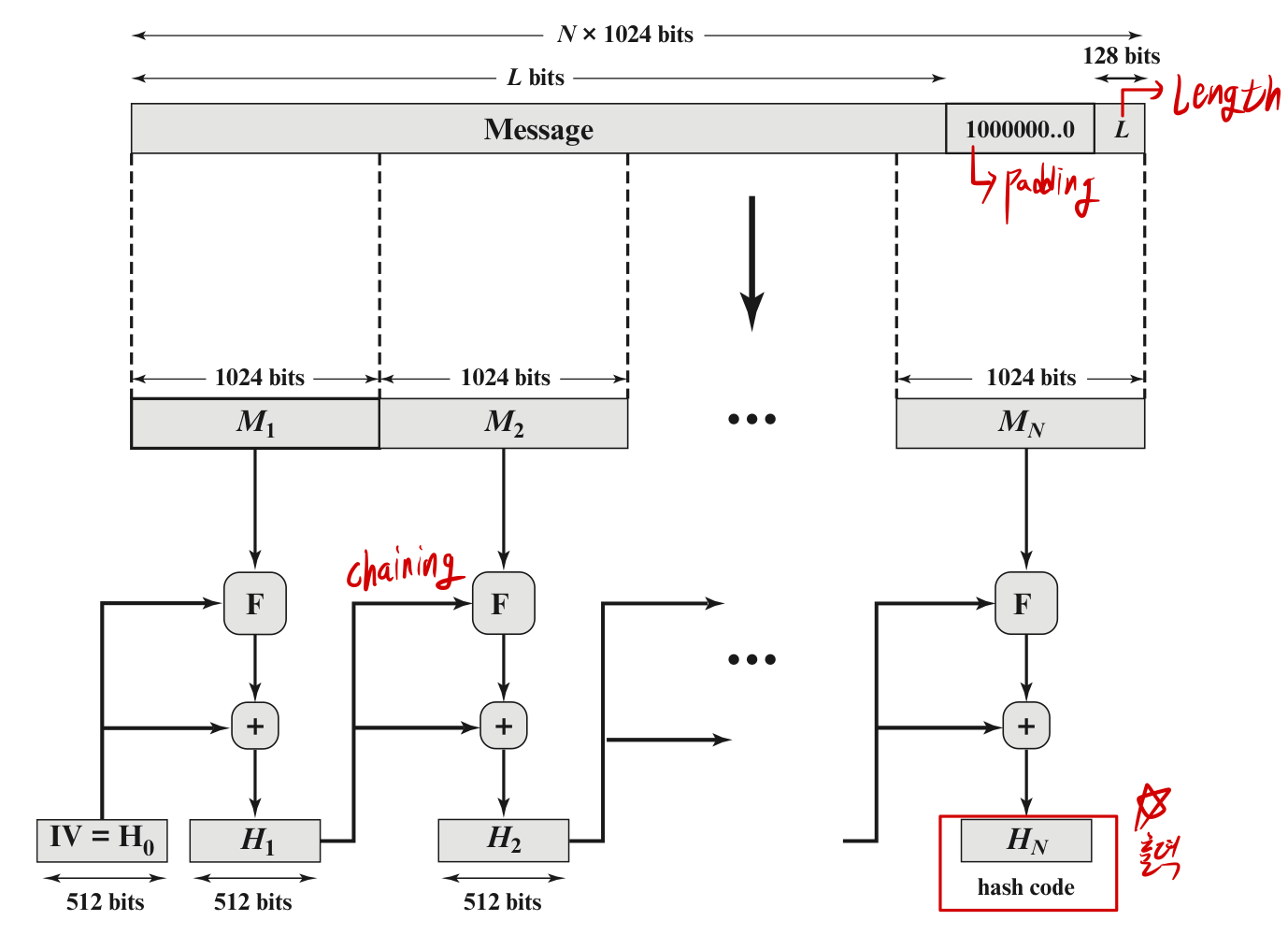
- SHA-512
- 입력 메시지 크기: 최대
2^128비트 이하 - 출력: 512비트 해시
- 처리 단위: 1024비트 블록
- 5단계 과정으로 구성된다: 패딩, 길이 추가, MD 버퍼 초기화, 블록 처리, 출력 생성
- 입력 메시지 크기: 최대
-
패딩 비트 붙이기 (1024의 배수로 만들어줌)
- 패딩은 첫번째 비트가 1이고 나머지 비트는 모두 0
-
길이 붙이기
- 128bit 크기의 길이정보 삽입
-
MD 버퍼 초기화
- 512 비트 버퍼를 해시함수의 중간 값과 최종 ...
-
1024비트 블록 메시지 처리
- F 함수
- 80 라운드로 구성
- 512비트 버퍼 값인 abcdefgh를 입력으로 사용하고 이 버퍼의 내용을 갱신
-
출력
- 메시지 다이제스트 출력
키는 사용하지 않는다는 것이 포인트
✏️ 메시지 인증 코드
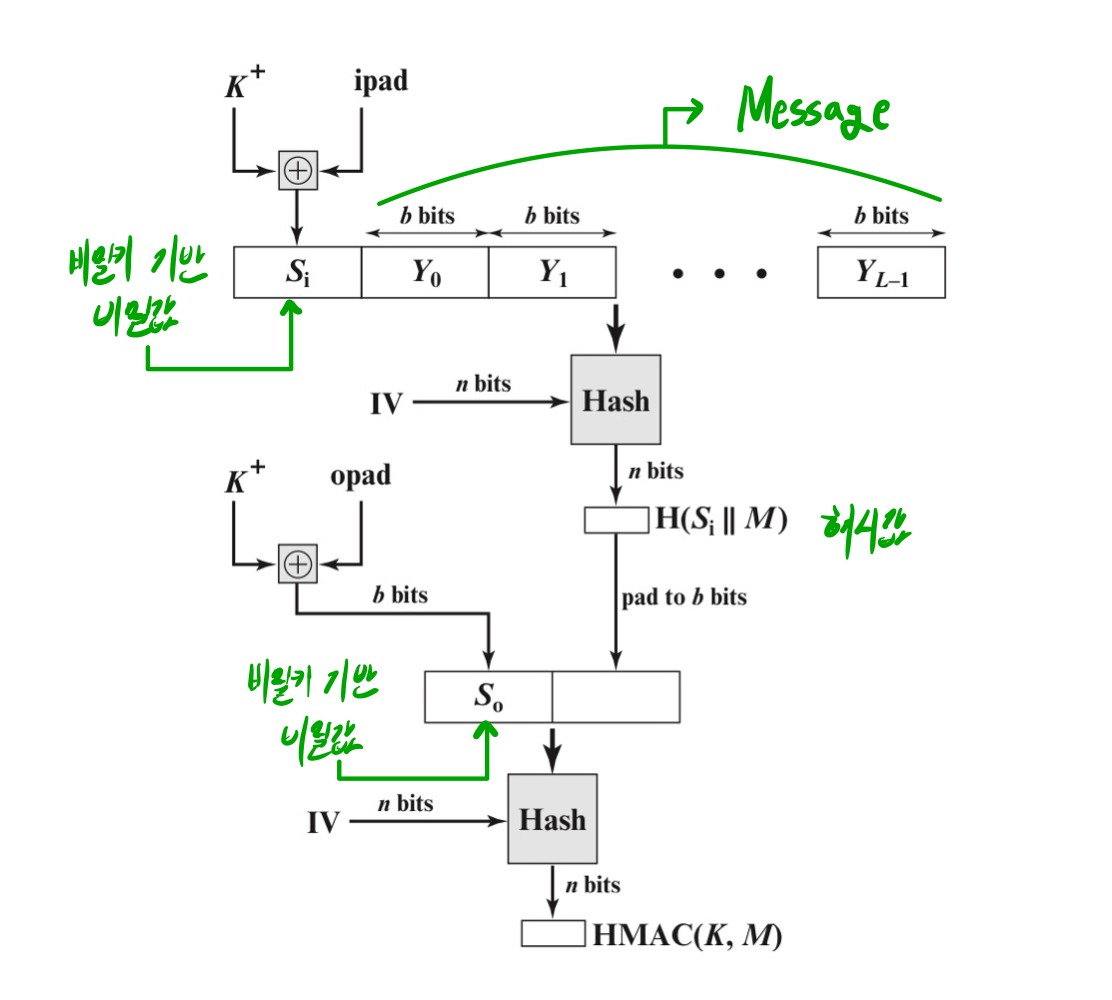
■ HMAC
HMAC은 기존 해시 알고리즘에 비밀키를 추가하여 메시지 인증을 수행하는 방식이다.
- 기존 해시 함수를 사용하면서도 비밀키를 적용하여 보안성을 높인다.
- DES와 같은 관용 암호 알고리즘보다 빠른 속도를 자랑한다.
H = 내장된 해시함수 ex) SHA-1
Y = M의 i번째 블록
b = 블록의 비트 수
n = 내장된 해시함수에 의해 생성된 해시코드의 길이
K = 비밀키
K+ = K의 왼쪽에 0을 붙여서 길이가 b가 되도록 만듦
ipad = 00110110
opad = 01011100
ipad는 ~opad이다
메시지 인증을 하기 위해서 HASH를 이용하는 방법이 있었다.
Nonce 붙이는 거
이건 아예 Hash 함수 자체만으로 인증이 되는 방식
■ CMAC
Cipher Based Message Authentication Code는 블록 암호를 기반으로 MAC을 생성하는 방식이다.
앞에서 본 Message를 암호화 한 방법 말고 다른거(얘는 메시지 전체를 DES해서 MAC을 붙이는 방식)
CMAC은 chaining을 적용함
메시지 길이가 블록 길이의 정수배인 경우
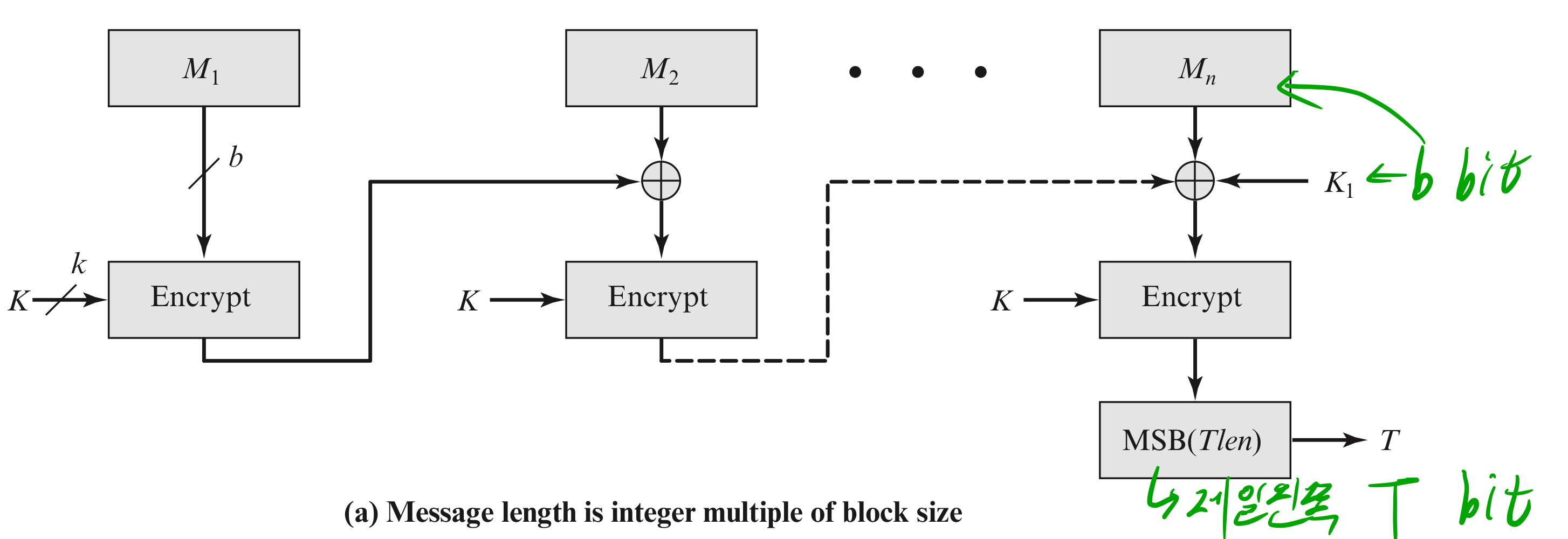
- 메시지를 n개의 블록으로 나누어 블록 암호화를 수행하고, 이를 기반으로 MAC을 생성한다.
- 메시지 길이가 블록의 정수 배가 아닐 경우 패딩을 추가하고, 마지막 블록에서는 다른 키(K2)를 사용한다.
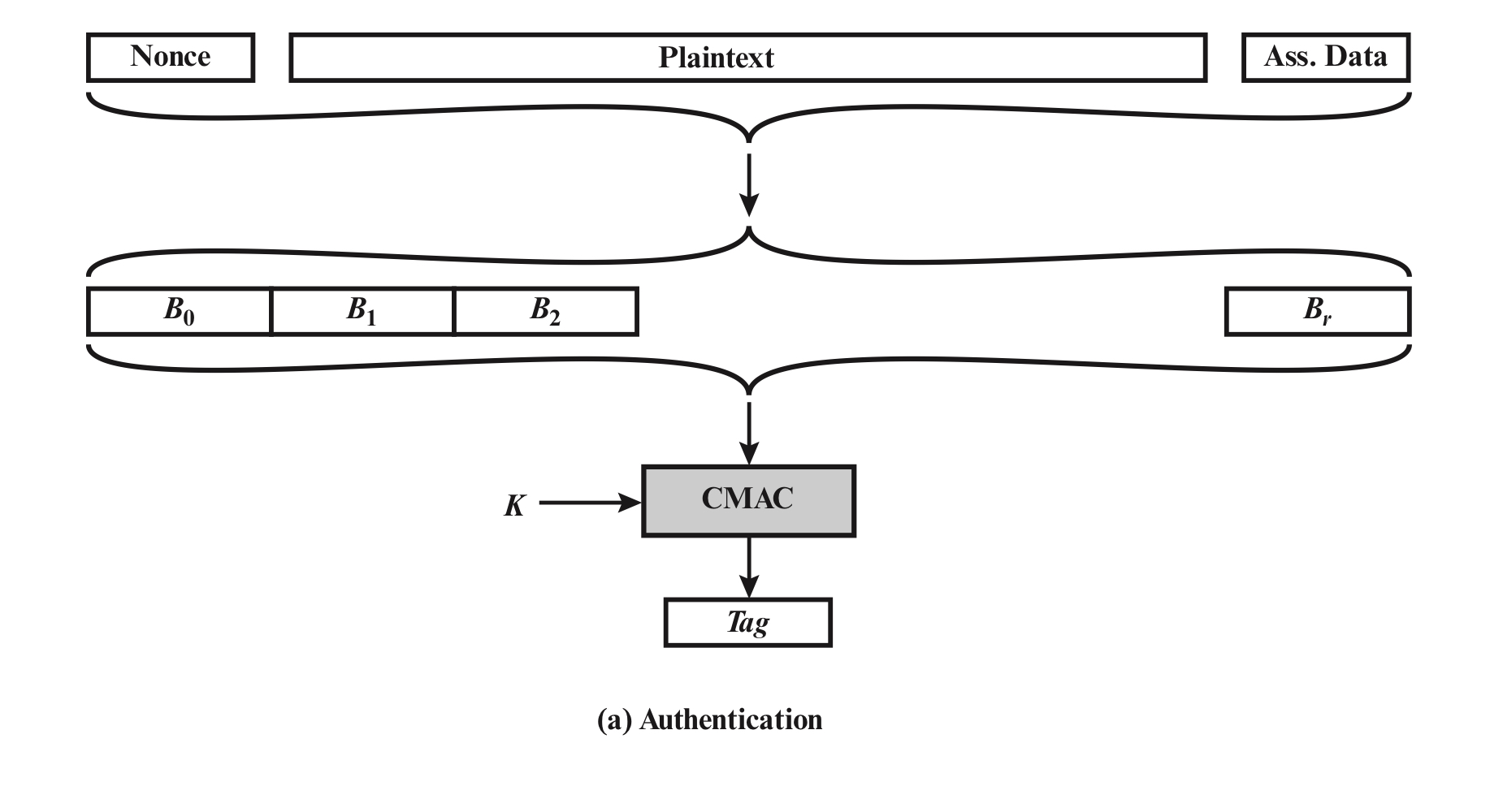
■ CCM
Counter Mode를 이용한 MAC 방식으로, 기밀성과 무결성을 동시에 보호한다.
필요한 기술들
- 인증된 암호화 모드
- 기밀성과 무결성(인증)을 동시에 보호해야 함
- AES, CTR, CMAC
- 암호화와 MAC 알고리즘에 동일한 단일 키 K 사용
- 비표
- Associated Data
- 암호화는 하지 않고 인증만 필요한 것
포인트
- Payload는 암호화와 인증이 필요하지만, 헤더는 인증만 필요하다.
✏️ 공개키 암호 원리
공개키 암호는 서로 다른 두 개의 키를 사용하는 비대칭 암호 방식이다.
- 공개키 암호가 관용 암호보다 더 안전하다 (X)
- 공개키 암호를 사용하게 되면서 관용 암호를 사용하지 않게 되었다. (X)
- 공개키를 사용하는 키 분배가 더 쉽다. (X)
공개키 방식이 관용 암호보다 오버헤드가 있다~ (O)
■ 공개키 암호의 핵심 요소
- 평문: 암호화 전의 원본 메시지
- 암호 알고리즘: 평문을 암호문으로 변환하는 알고리즘
- 공개키와 개인키: 서로 짝을 이루는 두 개의 키
- 암호문: 암호화된 메시지
- 복호 알고리즘: 암호문을 평문으로 변환하는 알고리즘
■ 공개키 암호의 특성
- 한 쌍의 키: 하나는 암호화, 다른 하나는 복호화에 사용된다.
- 공개키는 누구나 접근할 수 있도록 등록된다.
- 개인키는 암호문을 복호화하는 데 사용된다.
■ 공개키 암호의 요건
- 한 쌍의 키를 생성하는 것이 계산적으로 쉬워야 한다.
- 송신자는 암호문을 쉽게 생성할 수 있어야 한다.
- 수신자는 원문을 쉽게 복호화할 수 있어야 한다.
- 공격자가 개인키를 알아내는 것이 불가능해야 한다.
- 공개키로 암호문을 원문으로 변환하는 것이 불가능해야 한다.
■ 키 명칭
대칭 암호(관용 암호)
- 비밀키 또는 대칭키
공개키 암호
- 공개키
- 개인키
■ 응용
| 알고리즘 | 암호/복호 | 디지털 서명 | 키 교환 |
|---|---|---|---|
암호/복호: 수신자의 공개키로 메시지 암호화
디지털 서명(인증): 송신자 자신의 개인키로 암호화
키 교환: 세션 키를 공유
✏️ 공개키 암호 알고리즘
RSA
소인수분해 문제의 어려움을 기반으로 한 알고리즘
송신자와 수신자는 모두 n과 e를 알고있어야 함.
수신자만이 d값을 알아야 함.
공개키: e, n
개인키: d, n
C = M^e mod n
M = C^d mod n
RSA의 요구 조건
-
n보다 작은 모든 정수 M에 대해서 M = M^ed mod n을 만족하는 값 e,d,n을 구할 수 있어야 함
-
M^e와 c^d를 구하는 것이 쉬워야 함
-
e,n으로 d를 구하는 것이 어려워야 함
RSA 해독 방법
- brute force
- e와 d의 비트 수가 클수록 알고리즘은 안전
- n을 두개의 소인수의 곱으로 인수분해
- n = p * q
- 효과적인 인수분해 방법 없음
✏️ Diffie-Hellman
키 교환
두 사용자가 비밀키를 안전하게 교환해서 메시지를 암호화하려는 목적
이산 대수 문제를 푸는 것이 어렵다는 데 근거함
소수 p의 원시근(primitive root)
원시근: 자신의 거듭제곱을 이용하면 1부터 p-1까지의 정수를 모두 생성해 낼 수 있는 수
모두에게 알려진 정보
- 소수 q
- 의 원시근 a
- 공개키 Y
A는 랜덤넘버 X_A(X_A < q) 를 선택
B는 랜덤넘버 X_B(X_B < q) 를선택
A는 Y_a를 계산 Y_A = a^X_A mod q
B는 Y_b를 계산
이산대수
공식:
공개키: Y
개인키: X_A, X_B
공개키와 개인키를 이용해서 대칭키 교환을 함
대칭키: K = Y_B^X_A mod q
- q가 클수록 안전하다.
Y_A = a^X_A mod q,Y_B^X_A mod q등의 계산들은 쉽다.- X값을 찾는 것은 매우 어렵다.
man-in-the-middle attack에는 취약함
-> 인증이 안되었기 때문이다.
중간자 공격(man-in-the-middle)
중간자 == 공격자
- 공격자는 2개의 개인키와 공개키를 생성한다.
- A와 B의 공개키를 가로챈다.
- 자신의 공개키를 A와 B에게 분배한다.
- A와 D가 통신하고 B와 D가 통신한다.
메시지 위조가 가능
인증이 안되어서 발생한 문제이다!
해결방안: 전자 서명, 공개키 인증서를 사용
✏️ 기타 공개키 암호 알고리즘
DSS
- SHA-1를 사용한 전자 서명 기법
- 서명기능만 제공
-암호나 키 교환에 사용 못함
ECC
- 비트 수가 적어서 계산 속도가 빠름
- RSA와 동등한 안전성 제공
- 신뢰성이 RSA보다 낮음
✏️ 디지털 서명
메시의 출처와 메시지 내용에 대한 확신을 위해 메시지 전체를 암호화
- 메모리가 많이 소요됨
문서의 기능을 대신하는 작은 비트블록을 암호화
- 메시지 무결성은 보장하지만, 기밀성은 보장하지 못함
salt: 임의의 값이지만 A와 B가 모두 알아야 함.
해시 2번 거쳐서 나온 결과를
RSA 방식으로 A가 개인키로 암호화 해서 보냄
B는 A의 공개키로 까봄 (인증)
디지털 서명 자체는 무결성 + 기밀성인가? <- 공부 필요