[Algorithm] 정수 삼각형

문제 설명

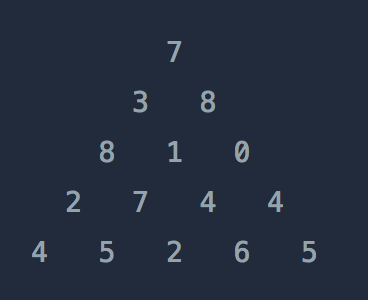
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

제한사항

삼각형의 높이는 1 이상 500 이하입니다.
삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.

입출력 예

triangle [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
result 30

접근하기

• DP 문제인지 모르겠어서 예전에 dfs로 풀려고 했던 기억이 있었는데 아쉽게도 그건 아니였다
• 위의 트리와 똑같이 생긴 모양의 dp 배열을 만들어 두고 각 위치까지 오는 길에 최대 값을 매번 갱신해나가면서 한다.
• dp는 큰 문제 하나를 풀기 위해 작은 문제로 쪼개서 그것들을 합쳐서 처리하는 느낌이다.
• 그래서 7부터 시작될 때, 3을 선택하면 10, 8을 선택하면 15를 저장하고 다음 8,1,0 자리에 가서 10일때 8이면? 10일 때 1이면? 15일때 1이면? 15일때 0이면 모두 생각해서 값을 갱신해준다.
• 그래서 결국 dfs로 풀면 중복 계산되는 루트들이 여러개 있는데 dp는 갱신 시마다 그걸 저장해두기에 순간 순간의 계산에 과거를 더하면 된다!

Code

class Solution {
    public int solution(int[][] triangle) {
        int[][] dp = new int[triangle.length][triangle.length]; 
        
        dp[0][0] = triangle[0][0];
        
        for(int i=1; i<triangle.length; i++){
            dp[i][0] = dp[i-1][0] + triangle[i][0];
            dp[i][i] = dp[i-1][i-1] + triangle[i][i];
        }
        
        for(int i=2; i<triangle.length; i++){
            for(int j=1; j<i; j++){
                dp[i][j] = Math.max(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j];
            }
        }
        
        int max = 0;
        
        for(int i=0; i<triangle.length; i++){
            if(max < dp[triangle.length-1][i]){
                max = dp[triangle.length-1][i];
            }
        }
        
        return max;
    }
    
    
}

문제 출처

• https://programmers.co.kr/learn/courses/30/lessons/43105?language=java