[알고리즘] 투 포인터(Two Pointers)

✋ 1차원 배열이 주어졌을 때, 특정 연속된 구간의 합이 M이 되는 경우의 수를 구하려면?

가장 단순하게는 2중 반복문을 돌리는 것이다.

public class Main{
	public static void main(String[] args){
		int[] arr = {1,2,3,4,2,5,2,3,1,1,2};
        int m = 5;
        
    	for(int i=0; i<arr.length; i++){
        	int sum = arr[i];
            
            for(int j=i+1; j<10; j++){
            	if(sum==m){
                	count++;
                }else if(sum>m){
                	break;
                }else{
                	sum+=arr[j];
                }
            }
        }
    }
}

아주 쉽게 볼수 있는 형태이다.
근데 이렇게 하면 시간복잡도가 O(N^2)이 나온다. (2중 반복문이니까)
배열의 크기가 커질 수록 느려지게 된다.

결국, 1차원 배열의 연속된 구간에 대해 2중 반복문을 개선하기 위해 나온 것이 투 포인터 알고리즘이다.

투 포인터 알고리즘

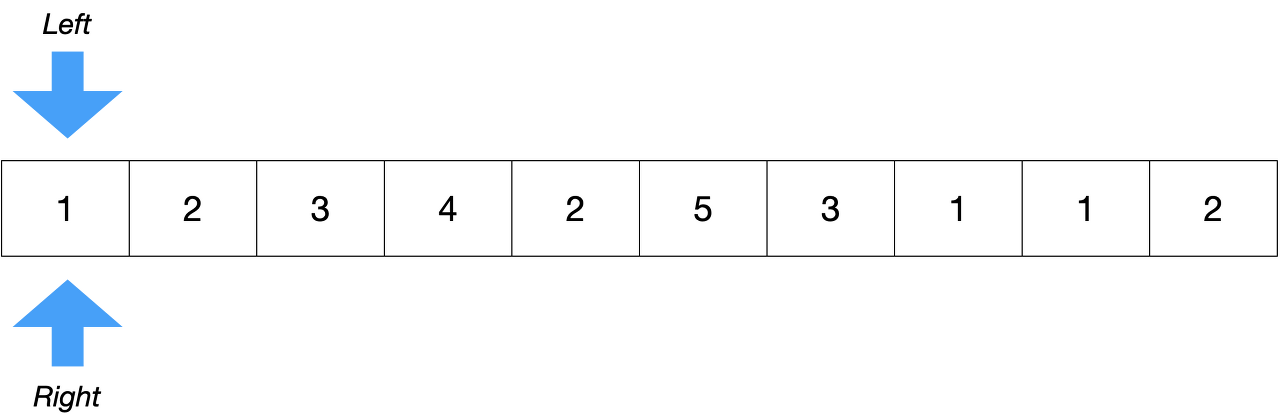
위와 같은 그림이 있다.

위의 1차원 배열에서 연속된 구간의 합이 5인 것의 경우의 수를 구해보자.

위의 2중 반복문과 큰 차이는 없지만, Right를 우측으로 하나씩 옮겨가면서 arr[left] + ... + arr[right]의 값이 5보다 크다면 더 이상 right를 옮기는 것은 무의미하다. right를 우측으로 옮겨봤자 마찬가지로 5보다 크기에.
그래서 이런 경우 left를 우측으로 옮긴다.

let's code it.

public class Main{
	public static void main(String[] args){
    	int[] arr = {1, 2, 3, 4, 2, 5, 3, 1, 1, 2};
        int m = 5;
        
		int count = twoPointer(arr, m);
	}
    
    public static int twoPointer(int[] arr, int m){
    	int sum =0, count =0;
        int left=0, right=0;
        
        while(true){
			if(sum>m){
            	sum -= arr[left++]; //left를 우측으로 옮기는 경우, left를 움직이면서 이전 위치에 있던 값을 합에서 빼줌.
            }else if(right==arr.length-1){
				break;
            }else{
            	sum += arr[right++]; //right를 우측으로 옮기는 경우
            }
            
            if(sum == m) count++;
        }
        
        return count;
    }
}

let's solve it.

완전 간단한 예제 문제를 풀어보자.

• https://www.acmicpc.net/problem/2018

package twoPointer;

import java.util.*;
public class boj_2018 {
    
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] arr = new int[n];
        for(int i=1; i<=n; i++) arr[i-1] = i;
        
        System.out.println(twoPointers(arr, n));
    }
    
    public static int twoPointers(int[] arr, int n){
        int sum=0, count=1;
        int left=0, right=0;
        
        while(true){
            if(sum>n){
                sum -= arr[left++];
            }else if(right == arr.length-1){
                break;
            }else{
                sum += arr[right++];
            }
            
            if(sum==n) count++;
        }
        
        return count;
    }
    
}