
정렬 별 장단점 비교
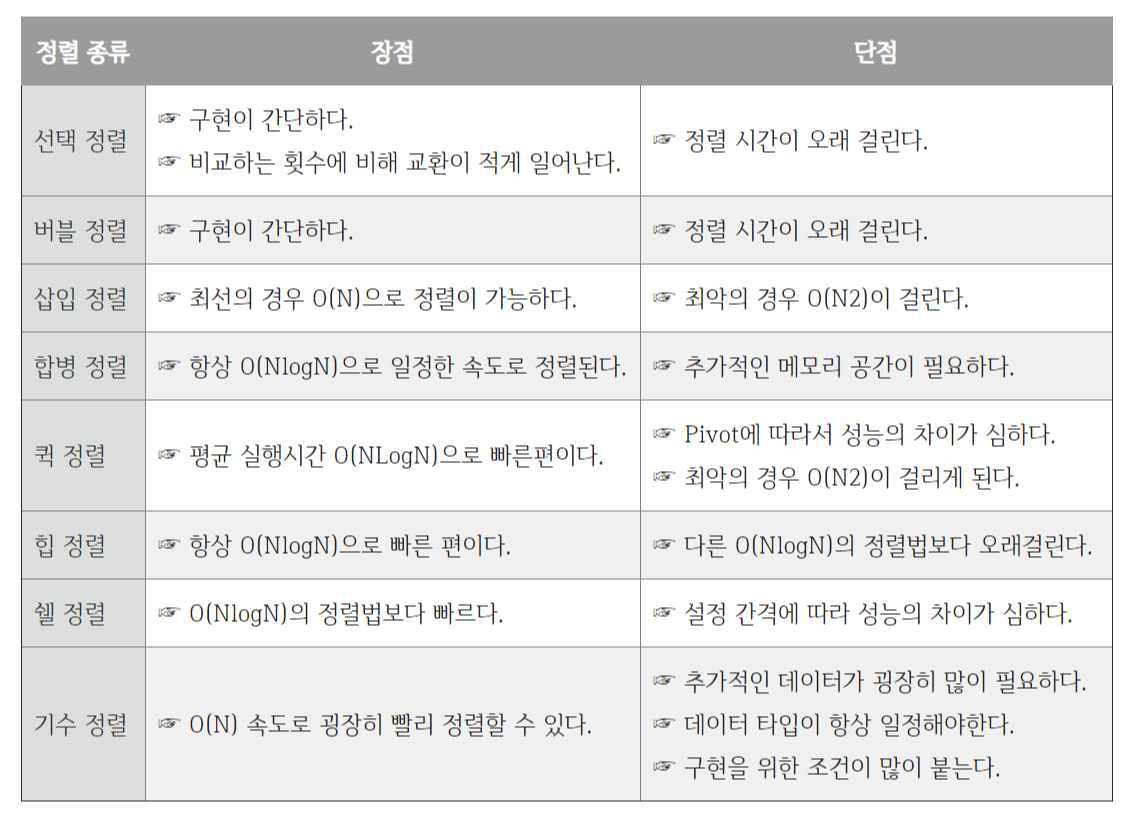
비교 표 출처 : [Algorithm] 각 정렬의 특징 및 장단점 & 시간복잡도
정렬 별 시간복잡도, 공간복잡도 비교
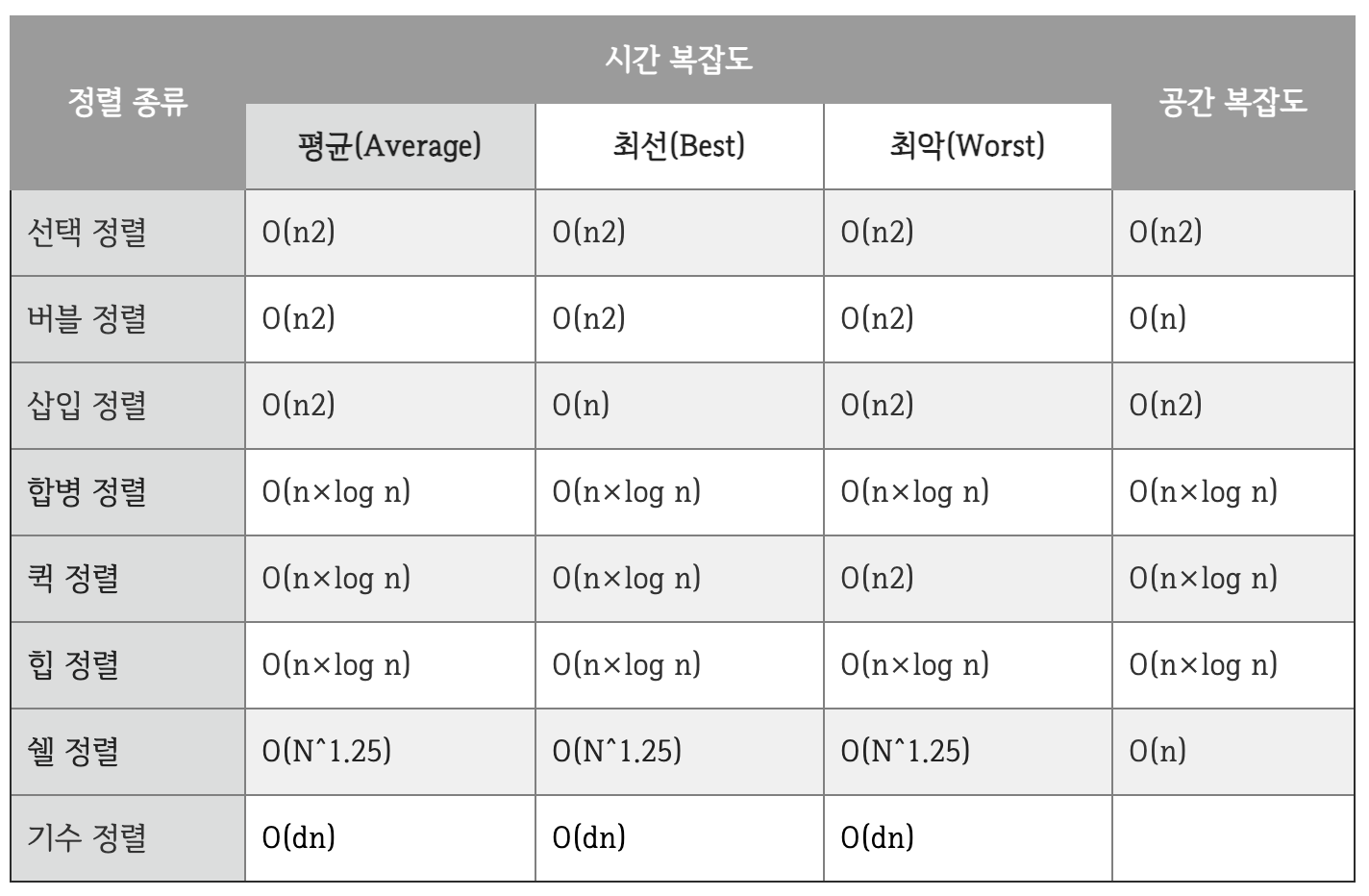
비교 표 출처 : [Algorithm] 각 정렬의 특징 및 장단점 & 시간복잡도
버블 정렬
" 인접 값끼리 비교하며 정렬. i를 length-i-1까지 올리는 정렬 "
장점
- 구현이 쉽다. 인접값만 비교하기에 쉽다. 코드가 직관적이다.
단점
- 비효율적이다. 최악, 최선 모두 O(N^2)의 시간복잡도를 갖기에 효율적인 정렬 방법은 아니다.
유용한 곳
- 이미 정렬된 데이터를 정렬 시에 가장 빠르다.(반대로 역순 배열은 가장 느리다)
선택 정렬
" standard로 값을 i로 저장하고 i보다 작으면 standard 바꾸면서 반복. 이 후 교환"
장점
- 구현이 쉬운편이다. 정렬을 위한 비교 횟수가 많지만 실제 교환 횟수는 적기에 많은 교환이 일어나야 하는 자료 상테에서 효율적일 수 있다.
- 버블 정렬과 똑같이 O(N^2)의 시간 복잡도를 갖지만 실제론 버블 정렬 보단 빠르다(장점인가)
단점
- 항상 O(N^2)의 시간복잡도를 갖는 오래 걸리는 정렬 방식.
유용한 곳
- 비교 횟수에 비해 적은 교환 횟수를 갖기에 많은 교환이 일어나야 하는 자료 상태에서 비교적 효율적.
퀵 정렬
" 피벗을 정하고 보다 작으면 왼쪽, 보다 크면 오른쪽. 계속 비교하면서 교환"
장점
- 기준 값(피벗)에 의한 분할을 통해 구현하는 정렬법으로써, 분할 과정에서 logN이라는 시간이 걸리게 되고 전체적으로 보게 되면 NlogN으로써 실행시간이 준수한 편이다.
단점
- 기준 값(피벗)에 따라 시간복잡도가 크게 다르다. 피벗을 적당한 값을 고르면 NlogN의 시간복잡도를 갖지만 최악의 경우 O(N^2)을 갖기도 한다...
- 불안정 정렬이다.
유용한 곳
- 순차 접근이 아닌 임의 접근이기에 LinkedList를 퀵 정렬에 사용하면 성능이 좋지 않다!
힙 정렬
" 최대 힙을 만들고 루트 노드 던지고 마지막 노드를 루트 노드 위치에 넣고 다시 최대 힙 만들기를 반복"
장점
- 추가 메모리가 필요치 앟ㄴ고 항상 O(NlogN)이라는 시간 복잡도를 갖는 정렬 법들 중 효율적이다. 퀵도 O(NlogN)을 가져서 매우 효율적이지만 피벗 값에 따라 O(N^2)까지도 갖지만 힙 정렬은 항상 O(NlogN)을 갖는다.
단점
- 이상적일 경우, 퀵 정렬과 비교했을 때 똑같이 O(NlogN)이 나오긴 하지만 실제론 퀵정렬보다 느리다고 한다. 데이터 상태에 따라 다른 정렬법에 비해 느린편이다.
- 불안정 정렬이다.
유용한 곳
- 가장 크거나 가장 작은 값을 구할 때!
- 최대 K만큼 떨어진 요소들을 구할 때 : 삽입 정렬보다 더욱 개선된 효과
삽입 정렬
"standard에 i번째 값 넣어두고 standard보다 크면 작은 거 나올 때까지 미루고 그 자리 차지."
장점
- 최선의 경우, O(N)이라는 엄청난 효율성을 가진다. 다른 정렬 알고리즘의 일부로도 쓰인다.
단점
- 최악의 경우, O(N^2)이라는 시간 복잡도를 갖는다. 데이터의 상태, 크기에 따라 성능 편차가 심하다..
유용한 곳
- 이미 정렬된 경우, 아주 최고의 정렬 알고리즘. 탐색을 제외한 오버헤드가 매우 적기에.
병합 정렬
"분할 분할 분할 정복 정복 정복"
장점
- 퀵 정렬과 비슷하게 원본 배열을 분할하면서 정렬하는 정렬법으로 분할 과정에서 logN만큼 시간이 걸린다. 최종적으로는 NlogN이 걸린다.
- 퀵 정렬과 다르게 피벗을 설정하거나 그런 과정 없이 무조건 절반으로 분할하기에 피벗에 따라 성능이 안 좋을 일은 없다. 따라서 항상 O(NlogN)이라는 시간 복잡도.
단점
- 퀵 보다 당연 좋다고 하겠지만 추가 메모리가 필요하다는 큰 단점이 있다.
- 임시 배열에 원본 맵을 계속해서 옮겨주면서 정렬하는 방법이다.
유용한 곳
- 순차적인 비교로 정렬하기에 LinkedList의 정렬에 사용하면 효율적이다.
- 크기가 큰 레코드 정렬 시 매우 효율적!
🖐 추가적인 메모리 할당할 수 없는 경우, 데이터가 최악으로 있다면 병합 vs 퀵 중에 뭘 써야 할까?
👉 데이터가 최악인 것만 본다면 퀵 보다 병합 정렬이 훨씬 빠르지만 추가 메모리 할당이 없다면 병합 정렬은 사용 불가이기에 퀵을 써야한다.
버블정렬은 최선의 경우 O(n) 이에요.