[알고리즘] 병합 정렬 (Merge Sort)

Jay·2021년 2월 27일

알고리즘-Concept

목록 보기

3/15

Intro

정렬 알고리즘은 아래와 같이 2가지로 나뉜다.

단순하지만 비효율적인 방법 : 선택 정렬, 삽입 정렬, 버블 정렬
복잡하지만 조금 더 효율적인 방법 : 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬

그 중 병합 정렬을 다뤄보자.

병합 정렬 (Merge Sort)

합병 정렬. 분할 정복 방법을 통해 구현한다.
빠른 정렬로 분류되며, Quick Sort와 함께 많이 언급되는 정렬 방식이다.
Quick Sort와는 반대로 안정 정렬에 속한다.

시간 복잡도

최악, 최선, 평균 모두 O(NlogN)
요소를 쪼갠 후에, 다시 합병 시키면서 정렬해 나가는 방식으로 쪼개는 방식은 퀵 정렬과 유사하다.

MergeSort()

private static void mergeSort(int[] a, int left, int right) {
        if (left < right) {
            int mid = (left + right) / 2;

            mergeSort(a, left, mid); // 왼쪽 부분 배열을 나눈다.
            mergeSort(a, mid + 1, right); // 오른쪽 부분 배열을 나눈다.
            merge(a, left, mid, right);
            // 나눈 부분 배열을 합친다.
            // 핵심 로직이다.
        }
    }

Merge()

/*
    * i : 왼쪽 부분 배열을 관리하는 인덱스
    * j : 오른쪽 부분 배열을 관리하는 인덱스
    * */
    private static void merge(int[] a, int left, int mid, int right) {
        int i, j, k, l;
        i = left;
        j = (mid + 1);
        k = left;

        // 왼쪽 부분 배열과 오른쪽 부분 배열을 비교하면서
        // 각각의 원소 중에서 작은 원소가 sorted 배열에 들어간다.
        // 왼쪽 혹은 오른쪽의 부분 배열 중 하나의 배열이라도 모든 원소가 sorted 배열에 들어간다면
        // 아래의 반복문은 조건을 만족하지 하지 않기 때문에 빠져 나온다.
        // sorted 배열에 들어가지 못한 부분 배열은 아래 쪽에서 채워진다.
        while (i <= mid && j <= right) {
            if (a[i] < a[j]) sorted[k++] = a[i++];
            else sorted[k++] = a[j++];
        }

        // mid < i 인 순간, i는 왼쪽 부분 배열의 인덱스를 관리하므로
        // 즉, 왼쪽 부분 배열이 sorted 에 모두 채워졌음을 의미한다.
        // 따라서 남아 있는 오른쪽 부분 배열의 값을 일괄 복사한다.
        if (mid < i) {
            for (l = j; l <= right; l++) sorted[k++] = a[l];
        } else {
            // mid > i 인 것은 오른쪽 부분 배열이 sorted 배열에 정렬된 상태로 모두 채워졌음을 의미한다.
            // 따라서, 왼쪽 부분 배열은 아직 남아 있는 상태이다.
            // 즉, 남아 있는 왼쪽 부분 배열의 값을 일괄 복사한다.
            for (l = i; l <= mid; l++) sorted[k++] = a[l];
        }

        // sorted 배열에 들어간 부분 배열을 합하여 정렬한 배열은
        // 원본 배열인 a 배열로 다시 복사한다.
        for (l = left; l <= right; l++) a[l] = sorted[l];
    }

코드로 이해가 안될 수 있다. 나 역시 처음엔 그림이 이해가 쉬웠다.

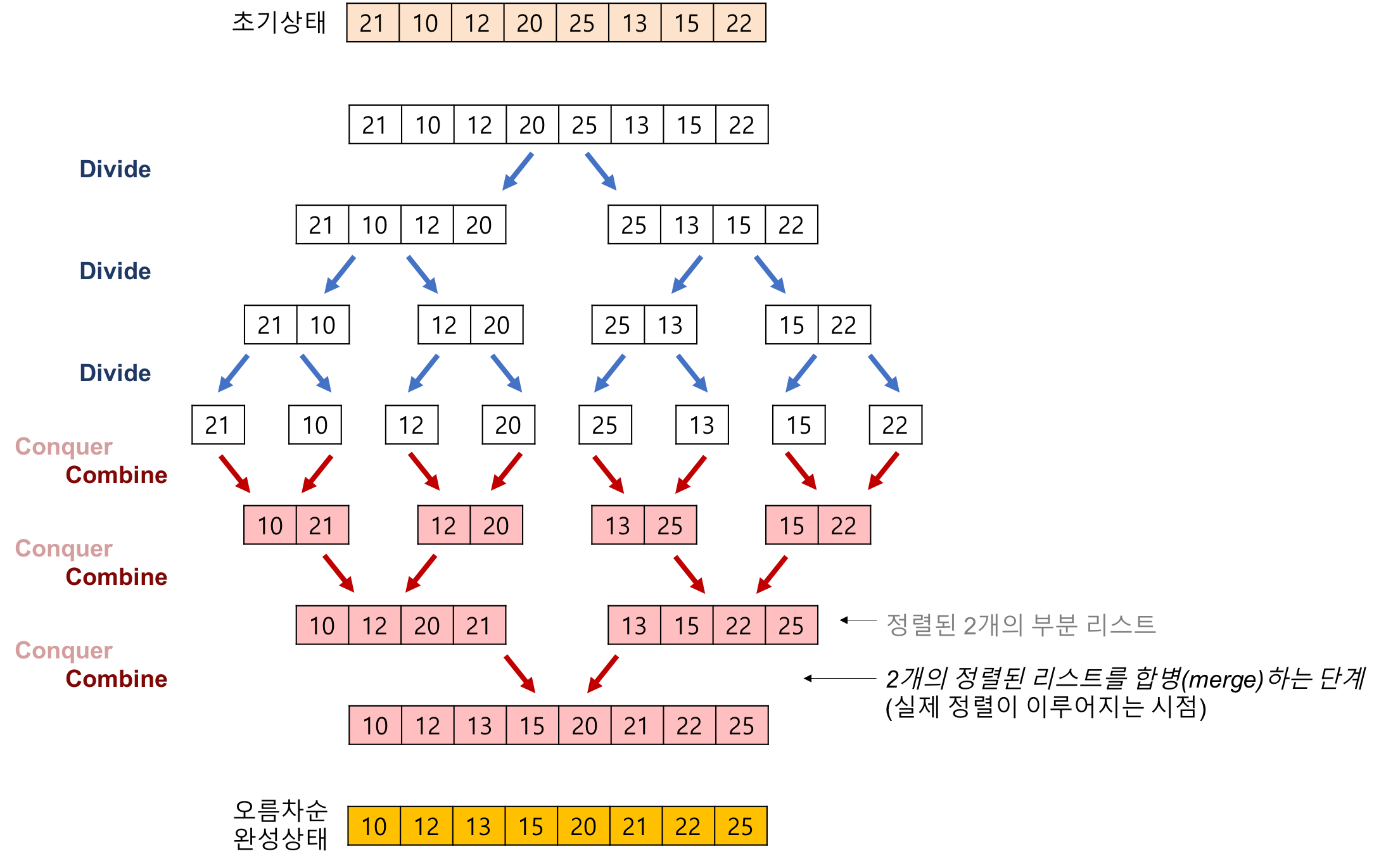
정말 기가막힌 설명을 해주는 그림이다.
분할과 정복을 반복한다.

합병 정렬은 순차적인 비교로 정렬을 진행하기에, LinkedList의 정렬에 사용하면 효율적이다.
퀵 정렬은순차 접근이 아닌 임의의 접근이기에 LinkedList를 퀵 정렬에 사용하여 정렬하면 성능이 좋지 않다.
LinkedList는 삽입과 삭제 연산에서는 유용하지만, 접근 연산에선 비효율적이다.