
힙 정렬 !?
- 완전 이진 트리를 기본으로 한느 힙 자료구조를 기반으로 한 정렬 방식.
- 불안정 정렬
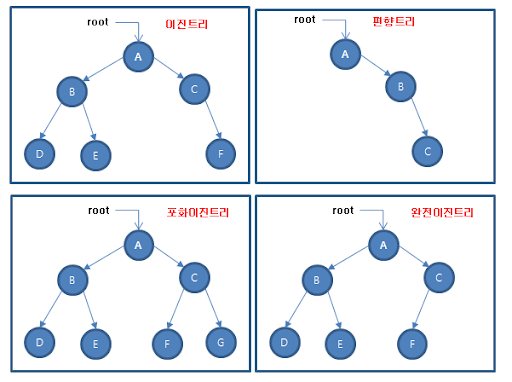
완전 이진 트리
- 삽입할 때, 왼쪽부터 차례대로 추가하는 이진 트리
시간 복잡도
- 평균 : O(NlogN)
- 최선 : O(NlogN)
- 최악 : O(NlogN)
로직
- 최대 힙을 구성한다.
- 현재 힙 루트는 가장 큰 값이 존재한다. 루트의 값을 마지막 요소와 바꾼 후, 힙의 사이즈를 하나 줄인다.
- 힙의 사이즈가 1보다 크면 위의 과정을 반복한다.
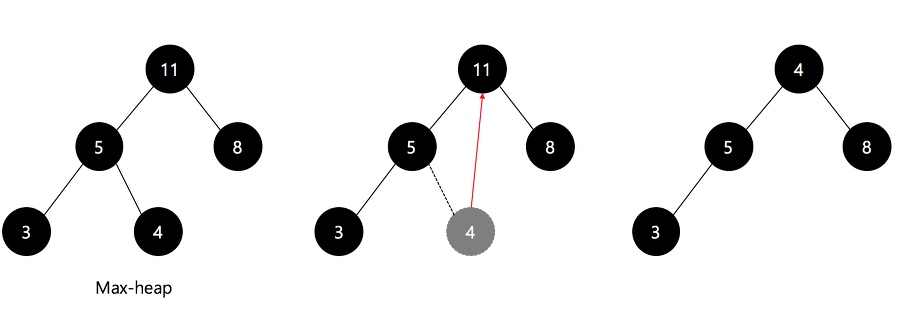
루트 노드를 마지막 노드로 대체한다. (11->4) 그리고 다시 최대 힙 구성.
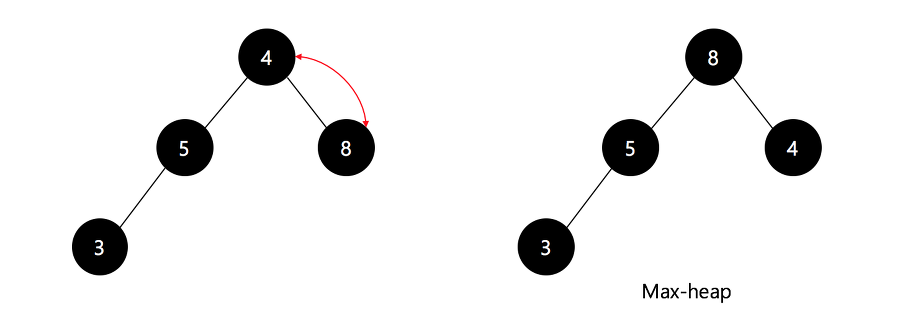
이와 같은 방식으로 최대 값을 하나씩 뽑아가면서 정렬하는 것이 Heap Sort.
private static void heapSort(int[] arr){
int n = arr.length;
for(int i=(n/2)-1; i>=0; i--{
heapify(arr, n, i);
}
for(int i= n-1; i>0; i--){
swap(arr, 0, 1);
heapify(arr, i, 0);
}
}1번째 heapify
- 일반 배열을 힙으로 구성하는 역할을 한다.
- 자식 노드로부터 부모 노드를 비교한다.
- (n/2)-1부터 0까지 인덱스를 돌리는 이유?
: 부모 노드의 인덱스를 기준으로 왼쪽 자식 노드 : ix2+1, 오른쪽 자식 노드 : ix2+2이기 때문에.
2번째 heapify
- 요소 하나가 제거된 이후에 다시 최대 힙을 구성하기 위함.
- 루트를 기준으로 진행한다.
private static void heapify(int[] arr, int n, int i){
int p = i; //부모 노드
int l = i * 2 + 1; // 왼쪽 자식 노드
int r = i * 2 + 2; // 오른쪽 자식 노드
//왼쪽 자식 노드와 부모 노드를 비교하며 큰 값을 부모 노드로 올린다.
if(l<n && arr[p] < arr[l]) p=l;
//오른쪽 자식 노드와 부모 노드를 비교하여 큰 값을 부모 노드로 올린다.
if(r<n && arr[p] < arr[r]) p=r;
//부모 노드를 가리키는 p 값이 바뀌면 위치를 교환하고
//heapify()를 호출하여 과정을 반복한다.
if( i != p ){
swap(arr, i, p);
heapify(arr, n, p);
}
}- 다시 최대 힙을 구성할 때까지 부모 노드와 자식 노드를 swap하며 재귀를 호출한다.
- 퀵 정렬과 합병 정렬의 성능이 좋기에 힙 정렬의 사용 빈도가 높진 않다.
- 하지만, 힙 자료 구조가 많이 사용되고 있으며, 이때 함께 따라오는 개념이 heap sort이다.
Heap Sort가 유용 할 때
- 가장 크거나 가장 작은 값을 구할 때 : 최소 힙, 최대 힙의 루트 값이기에 한번의 힙 구성을 통해 구하는 것이 가능하다.
- 최대 k만큼 떨어진 요소들을 정할 때 : 삽입 정렬보다 더욱 개선된 효과를 볼 수 있따.
참고로, PriorityQueue가 힙으로 구성되어있다.😎