선택 정렬
-
정렬(sorting)이란 데이터를 특정한 기준에 따라 순서대로 나열하는 것을 말함
-
문제 상황에 따라 적절한 정렬 알고리즘이 공식처럼 사용됨
- 데이터의 개수가 적을 때, 데이터의 개수가 많지만 데이터의 범위가 특정범위로 한정되어 있을 때, 이미 데이터가 정렬되어 있는 경우 등
-
선택 정렬
- 처리되지 않은 데이터 중 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸는 것을 반복 → 매번 현재 범위에서 가장 작은 데이터를 골라 맨 앞으로 보내주는 것
-
선택 정렬 동작 예시
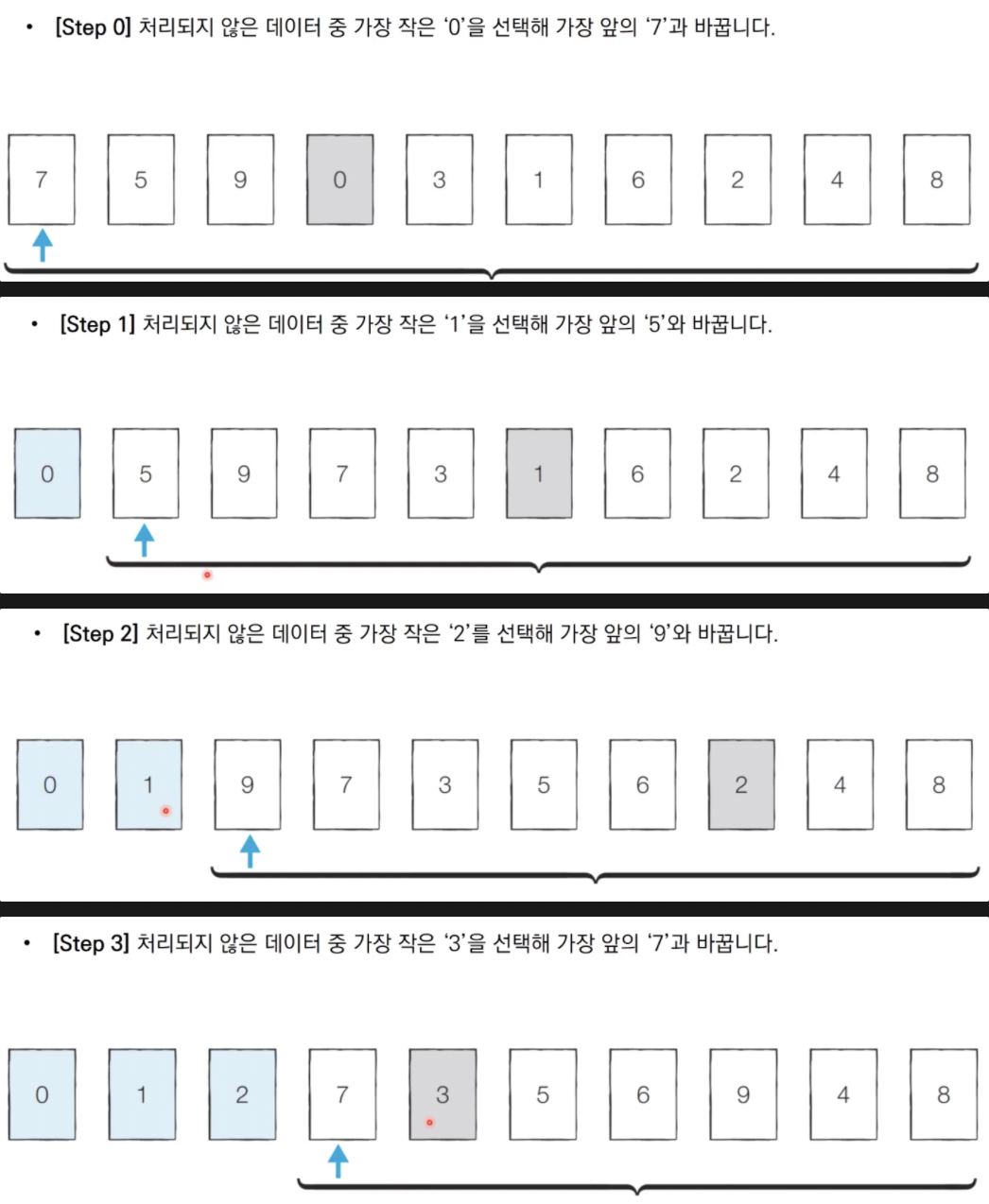
- 이러한 과정을 반복하면 정렬이 완료됨

- 탐색 범위는 반복할 때마다 줄어들고 매번 가장 작은 원소를 찾기 위해 탐색 범위만큼 데이터를 하나씩 확인하기에 매번 선형탐색을 수행하는 것과 동일 → 이중반복문을 이용해서 선택정렬 구현
- 이러한 과정을 반복하면 정렬이 완료됨
-
코드
array = [7,5,9,0,3,1,6,2,4,8] #i는 반복할 때마다 가장 앞쪽의 위치 for i in range(len(array)): min_index = i # 가장 작은 원소의 인덱스 for j in range(i+1, len(array)): if array[min_index] > array[j]: min_index = j array[i], array[min_index] = array[min_index], array[i] # 스와프: 가장 앞쪽 원소와 가장 작은 원소의 위치를 바꿔줌 print(array) -
선택 정렬의 시간 복잡도
- N번만큼 가장 작은 수를 찾아서 맨 앞으로 보내야 함
- 전체 연산 횟수: N + (N-1) + (N-2) + … + 2 (맨 마지막은 연산 안해줘도 됨)
- 이는 (N^2 + N -2) / 2로 표현할 수 있는데 빅오 표기법에 따라 O(N2)이라고 작성함
삽입 정렬
-
처리되지 않은 데이터를 하나씩 골라 적절한 위치에 삽입
-
데이터는 어느위치에 들어가는 것이 맞을것인가 매번 계산해서 적절한 위치에 삽입
-
선택 정렬에 비해 구현 난이도가 높지만 더 효율적임
-
삽입 정렬 동작 예시

- 이러한 과정을 반복하면 다음과 같이 정렬이 완료됨

- 이러한 과정을 반복하면 다음과 같이 정렬이 완료됨
-
코드
array = [7,5,9,0,3,1,6,2,4,8] #두번째 원소부터 시작해서 왼쪽으로 이동해나가며 위치를 바꿔주는 것을 이용 for i in range(1, len(array)): for j in range(i, 0, -1): #인덱스 i부터 1까지 1씩 감소하며 반복하는 문법 if array[j] < array [j-1]: #한 칸씩 왼쪽으로 이동 (위치를 바꿈) array[j], array[j-1] = array[j-1], array[j] else: #자기보다 작은 데이터를 만나면 그 위치에서 멈춤 break print(array) -
삽입 정렬의 시간 복잡도
- 시간복잡도는 O(N^2)이며, 선택 정렬과 마찬가지로 반복문이 두번 중첩되어 사용됨
- 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 동작함
- 최선의 경우 O(N)의 시간 복잡도를 가짐
- 이미 정렬되어 있는 상태에서 삽입 정렬을 수행하면?
- 각 원소가 들어갈 위치를 고를 때 선형탐색을 수행하게 되는데 그 탐색과정이 바로 멈춰지기에 데이터가 어디로 들어갈지 고르는 시간이 상수시간으로 대체되기에 전체 정렬을 위한 복잡도가 O(N)이 됨
퀵 정렬
-
기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법
-
일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘 중 하나, 병합 정렬과 더불어 프로그래밍 언어의 정렬 라이브러리의 근간이 되는 알고리즘
-
가장 기본적인 퀵 정렬은 첫번째 데이터를 기준 데이터(Pivot)로 설정함
-
퀵 정렬 동작 예시

-
왼쪽은 모두 피벗값보다 작은 데이터, 오른쪽은 모두 피벗값보다 큰 데이터

-
-
퀵 정렬이 빠른 이유: 이상적인 경우 분할이 절반씩 일어난다면 전체 연산 횟수로 O(NlogN)
- 너비 높이 = N logN = NlogN
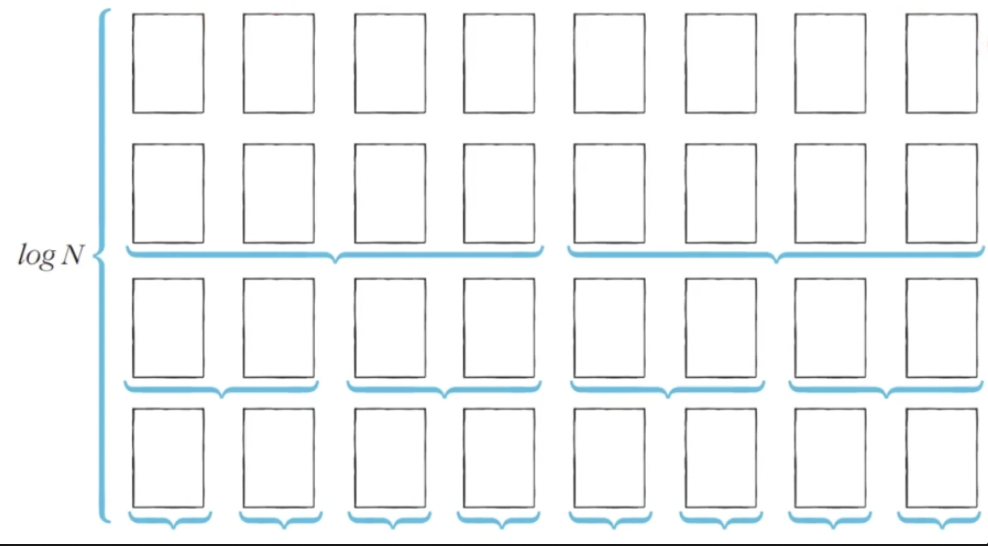
- 너비 높이 = N logN = NlogN
-
퀵 정렬의 시간 복잡도
- 평균의 경우 O(NlogN)의 시간복잡도를 가짐
- 최악의 경우 O(N^2)의 시간 복잡도를 가짐
- 이미 정렬된 배열에 대해 첫번째 원소를 피벗으로 삼아 퀵 정렬을 수행하면 분할이 수행되는 횟수가 N이 되어 분할을 하기 위해 매번 선형탐색을 해야하기에 시간복잡도가 N^2이 됨
-
코드
array = [5,7,9,0,3,1,6,2,4,8] def quick_sort(array): # 리스트가 하나 이하의 원소만을 담고 있다면 종료 if len(array) <= 1: return array pivot = array[0] # 피벗은 첫번째 원소 tail = array[1:] # 피벗을 제외한 리스트 left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분 right_side = [x for x in tail if x >= pivot] # 분할된 오른쪽 부분 # 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행하고, 전체 리스트 반환 return quick_sort(left_side) + [pivot] + quick_sort(right_side) print(quick_sort(array))
계수 정렬
-
특정한 조건이 부합할 때만 사용할 수 있지만 매우 빠르게 동작하는 정렬 알고리즘
- 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때 사용 가능
-
데이터의 개수가 N, 데이터(양수) 중 최댓값이 K일 때 최악의 경우에도 수행 시간 O(N+K) 보장
-
계수 정렬 동작 예시
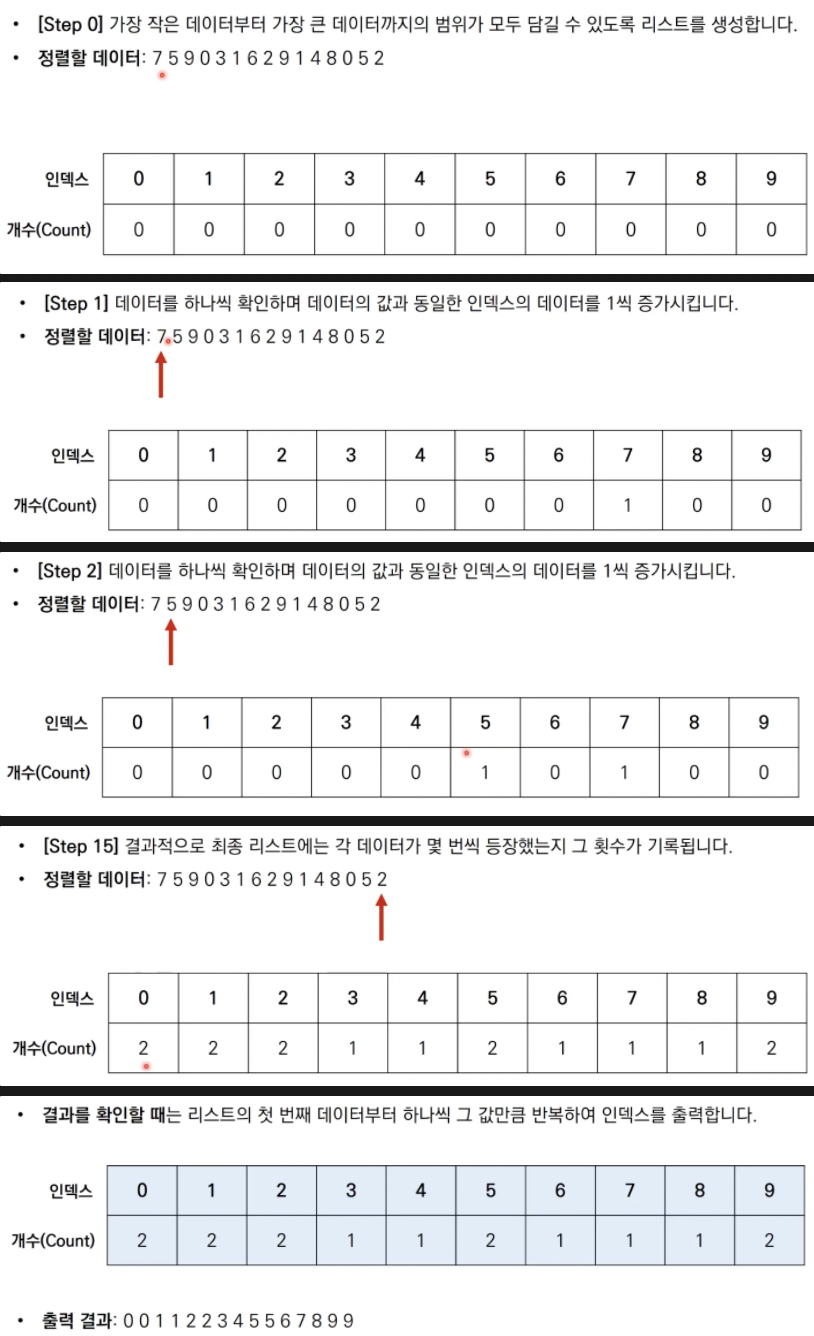
-
가장 작은 데이터부터 큰 데이터까지 모든 범위를 포함하는 배열을 만들기에 공간 복잡도는 높지만 빠르게 동작함
-
코드
# 모든 원소의 값이 0보다 크거나 같다고 가정 array = [7,5,9,0,3,1,6,2,9,1,4,8,0,5,2] # 모든 범위를 포함하는 리스트 선언(모든 값은 0으로 초기화) count = [0] * (max(array) + 1) for i in range(len(array)): count[array[i]] += 1 # 각 데이터에 해당하는 인덱스의 값 증가 for i in range(len(count)): # 리스트에 기록된 정렬 정보 확인 for j in range(count[i]): print(i, end='') # 띄어쓰기를 구분으로 등장한 횟수만큼 인덱스 출력 -
계수 정렬의 복잡도 분석
- 시간 복잡도와 공간 복잡도는 모두 O(N+K)
- 때에 따라 심각한 비효율성을 초래할 수 있음
- 데이터가 0과 999,999로 단 2개만 존재하는 경우 100만개의 배열을 만들어야하기에 비효율적임
- 동일한 값을 가지는 데이터가 여러개 등장할 때 효과적으로 사용할 수 있음
- ex) 성적의 경우 100점을 맞은 학생이 여러 명일 수 있기에 계수 정렬이 효과적임 (데이터의 값 범위가 한정적이면서 정렬할 데이터가 많은 경우)
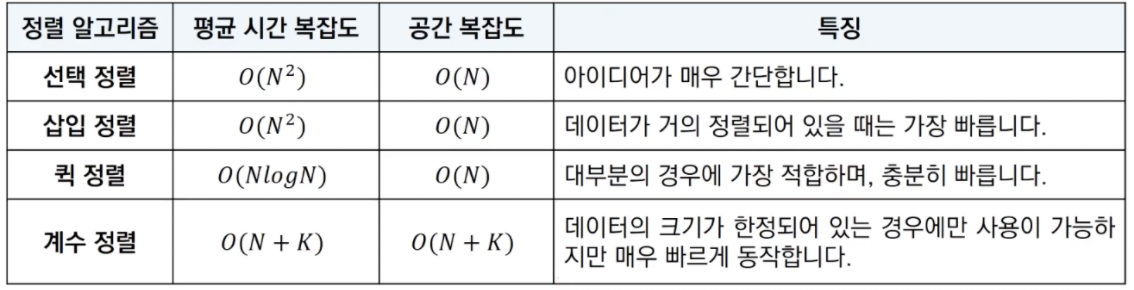
정렬 알고리즘 비교 및 기초 문제 풀이
-
대부분의 프로그래밍 언어에서 지원하는 표준 정렬 라이브러리는 최악의 경우에도 O(NlogN)을 보장함
<문제> 두 배열의 원소 교체

- 문제 해결 아이디어
- 매번 배열 A에서 가장 작은 원소를 골라서, 배열 B에서 가장 큰 원소와 교체
- 가장 먼저 배열 A와 B가 주어지면 A에 대하여 오름차순 정렬하고, B에 대하여 내림차순 정렬함
- 두 배열의 원소를 첫번째 인덱스부터 차례로 확인하면서 A의 원소가 B의 원소보다 작을 때에만 교체를 수행
- 두 배열의 원소가 최대 100,000개까지 입력될 수 있으므로 N^2으로 동작하는 선택정렬과 같은 알고리즘을 이용했을 때 시간초과 판정을 받을 수 있음
- 따라서 최악의 경우에도 O(NlogN)을 보장하는 정렬 알고리즘을 이용해야 함 → 표준라이브러리 사용
- 답안 예시
n, k = map(int, input().split()) # N, K 입력 a = list(map(int, input().split()) # 배열 A의 모든 원소 입력 b = list(map(int, input().split()) # 배열 B의 모든 원소 입력 a.sort() # 배열 A는 오름차순 정렬 b.sort(reverse=True) # 배열 B는 내림차순 정렬 수행 # 첫번째 인덱스부터 확인하며, 두 배열의 원소를 최대 K번 비교 for i in range(k): # A의 원소가 B의 원소보다 작은 경우 if a[i] < b[i]: # 두 원소를 교체 a[i], b[i] = b[i], a[i] else: # A의 원소가 B의 원소보다 크거나 같을 때, 반복문 탈출 break print(sum(a))
참고: 이것이 취업을 위한 코딩 테스트다 with 파이썬 (취업과 이직을 결정하는 알고리즘 인터뷰 완벽 가이드), 유튜브 강의 영상