밑바닥부터 시작하는 딥러닝 #3-4 경사법

Prologue

나는 여전히 웹개발자이지만, 회사에 부쩍 딥러닝 과제가 많아져서 딥러닝 공부가 많이 필요하게 됐다. 밑바닥부터 시작하는 딥러닝 책이 좋다고 해서 천천히 하나하나 공부해보려 한다.

경사법(경사하강법)

기계학습 문제 대부분은 학습 단계에서 최적의 매개변수(가중치, 편향)를 찾아야 합니다. 최적이란 손실 함수가 최솟값이 될 때의 매개변수 값 입니다.

기울기를 잘 이용해 손실 함수의 최솟값을 찾으려는 것이 경사법 입니다.

일반적으로 손실 함수의 값을 낮추는 방향은 기울기가 향하는 방향 이지만, 복잡한 함수에서는 기울기가 가리키는 방향에 최솟값이 없는 경우가 대부분 입니다.

또 기울기가 0이어도 반드시 최솟값은 아닙니다. 안장점(극솟값이라고도 하며 부분적인 최솟값을 말합니다.), 복잡하고 찌그러진 함수에서는 고원이라 하는 학습 정체기에 빠질 수도 있습니다.

경사법은 최솟값을 찾냐, 최댓값을 찾냐에 따라 이름이 다른데, 전자를 경사 하강법, 후자를 경사 상승법이라 합니다. 단, 부호의 차이라 두 용어의 차이는 별로 중요하지 않습니다.

수식

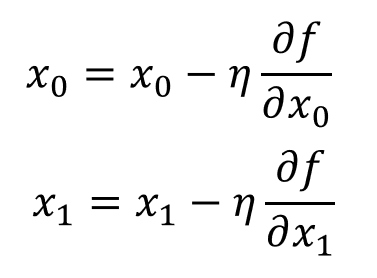
수식은 위와 같고, 위 수식에서 에타가 의미하는 것은 학습률(learning rate) 입니다. 학습률을 잘 지정해주는 것은 매우 중요합니다.

테스트

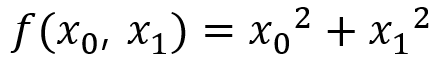
위 수식의 최솟값을 구해봅시다. 사실 구하지 않아도 직관적으로 0이 최솟값이라는걸 알긴 합니다.

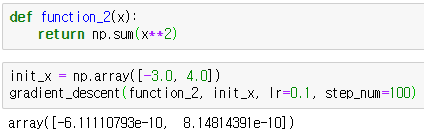
위의 결과 값을 보면 0과 매우 근사한 값이 나온 것을 알 수 있습니다.

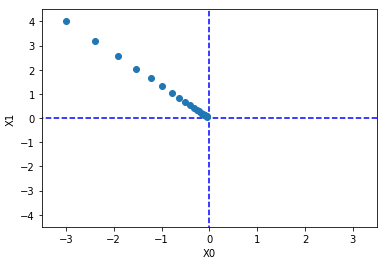
위는 경사하강법으로 올바른 최솟값에 찾아가는 과정을 시각화 한 것입니다.

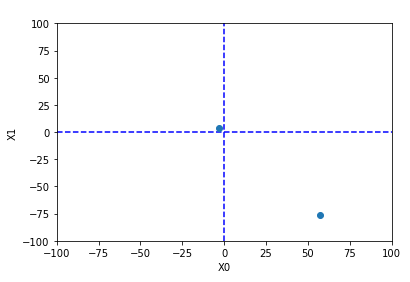
위는 학습률(learning rate)에 매우 큰 값을 넣은 경우입니다. 크게 발산하는 것을 볼 수 있습니다.

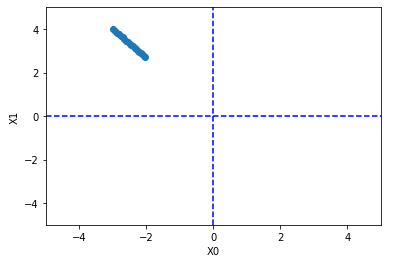
위는 학습률(learning rate)에 매우 작은 값을 넣은 경우입니다. 올바른 값에 찾아가기 전에 학습이 끊깁니다.

사람이 직접 설정하는 매개변수를 하이퍼 파라미터 라고 합니다. 이 값은 시험을 통해 가장 잘 학습하는 값을 찾는 과정을 거쳐야 합니다.

신경망에서의 기울기

이전에는 입력인 2개의 함수의 기울기를 이용해서 해당 함수의 최솟값으로 가도록 하강시켰습니다.

신경망에서의 기울기는 가중치 매개변수에 대한 손실 함수의 기울기 입니다.

수식

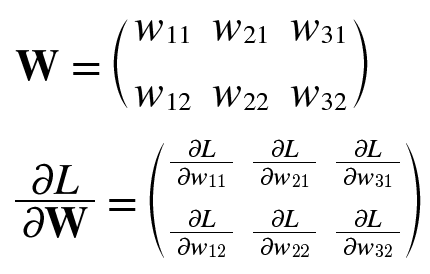
L은 손실 함수이며, W는 가중치입니다. 가중치 매개변수에 대한 손실함수의 경사(기울기) 는 각각을 편미분하여 위의 수식처럼 구할 수 있습니다.

가중치 매개변수에 대한 손실함수의 기울기의 형상과 가중치의 형상이 같다는 것을 알아두어야 합니다.

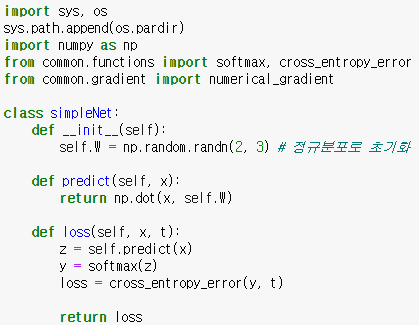
위는 simpleNet이라는 간단한 신경망 예제입니다.

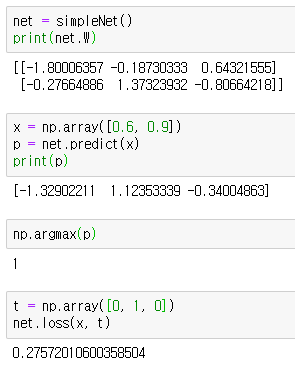
위는 simpleNet에 있는 몇가지 함수들의 실행 결과입니다.

predict는 입력과 가중치의 연산 결과를 계산해주고, loss는 정답 레이블을 이용하여 손실함수의 값을 계산해줍니다.

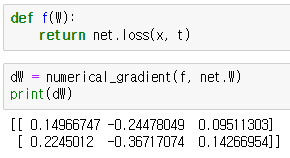
dW 값은 net 클래스에 있는 가중치(W)를 편미분한 것 즉, 기울기입니다. 이 기울기가 뜻하는 것은 만일 첫번째 가중치(W11)을 h만큼 증가시키면, 약 0.149h 정도 손실함수의 값이 증가한다는 뜻입니다. 두번째 가중치(W12)의 경우는 가중치를 h만큼 증가시키면 약 -0.244h 정도 손실함수의 값이 감소합니다. 첫번째 가중치는 양의 방향으로 갱신해야 하고 두번째 가중치는 음의 방향으로 갱신해야 함을 알 수 있습니다. 그리고 영향력은 두번째 가중치가 더 크게 기여한다는 사실도 알 수 있습니다.

간단한 람다 활용법

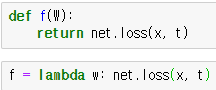
위의 방식으로도 함수 정의를 할 수 있지만, 람다를 이용하면 조금 더 간단하게 함수를 정의할 수 있습니다.

정리

• 학습은 손실함수의 값을 최소화하는 매개변수(가중치, 편향)를 찾아내는 일을 말합니다.
• 기울기를 이용하여 손실함수의 최솟값을 찾으려는 시도를 경사법이라고 합니다.
• 손실 함수가 최저가 되는 점은 대부분 기울기가 향하는 방향인데, 복잡한 함수의 경우엔 그렇지 않은 경우가 많습니다.
• 기울기가 0인 지점이 꼭 최소값은 아닙니다. 안장점(국소적인 최솟값)이라는 함정이 있습니다.
• 학습률은 하이퍼파라미터라고 불리며, 사람이 직접 테스트를 통해 설정해주어야 합니다.
• 신경망에서 기울기는 가중치 매개변수에 대한 손실함수의 기울기입니다.
  • (Loss/Weight) 각각 미분한 값을 넣음