자바스크립트로 알고리즘 정리하기 #10 다이나믹 프로그래밍 문제풀이 1

자바스크립트로 알고리즘 정리하기 #10 다이나믹 프로그래밍 문제풀이 1

1로 만들기 (boj 1463)

문제 링크

1. X가 3으로 나눠 떨어지면 3으로 나누기
2. X가 2로 나눠 떨어지면 2로 나누기
3. 1을 빼기

위와 같은 3가지 연산이 있을 때 X를 가장 빨리 1로 만드는 연산 횟수를 구하는 문제이다.

일반적인 접근 방식

• N을 1로 만들려고 한다.
• N을 가장 빠르게 작게 만들어야 한다.
• 3으로 나누는 것이 수를 가장 빠르게 작게 만든다.
• 3으로 나누는 것, 2로 나누는 것, 1을 빼는 우선순위로 N을 1로 만들어본다.

점화식 만들어보기

• N을 1로 만드는 최소 연산횟수 구해보기
  • D[N]은 N을 1로 만드는 최소 연산 횟수
  • 이렇게 연산의 3가지 방법을 주는 것은 사실 매우 난이도가 쉬운 문제이다.
  • 1번 N/3을 1로 만드는 최소 연산 횟수는 D[N/3]이다.
  • 2번 N/2을 1로 만드는 최소 연산 횟수는 D[N/2]이다.
  • 3번 1 + D[N-1]로 1로 만드는 최소 연산 횟수를 유도해볼 수 있다.

풀이 소스

bottom-up 방식으로 풀어낸다. 풀이의 핵심은 N이 가장 작은 2일 때부터 계속 최소 값을 쌓아나가는 것이다.

1일 때는 굳이 무언가 변화를 줄 필요도 없으니, 연산 횟수 자체가 존재하지 않는다. N일 때 최소 연산 횟수를 구하는데는 최단거리의 원리와 같은 원리를 사용한다.

서울, 강원, 대전, 대구, 구미, 포항, 부산 지역이 있을 때 서울에서 부산을 가는 최단거리가 서울 -> 대전 -> 대구 -> 부산 이라면, 대전에서 부산을 가는 최단거리는 대전 -> 대구 -> 부산 일 것이다. 이렇게 부분의 정답이 전체의 정답에 기여할 수 있다. 문제의 정답을 작은문제의 정답으로부터 구할 수 있다.

여기서는 2부터 N까지 계속해서 숫자 1로 만드는 최소 연산횟수를 쌓아나가는 것이다. 이렇게 쌓아놓으면 N이 100000이 됐다고 했을 때, 우리가 검증해야 할 값은

N이 2로 나누어 떨어지니 N/2, 50000일 때의 최소 연산 횟수 + 1(나누기 연산)
N에 N-1을 하여 99999일 때의 최소 연산 횟수 + 1(나누기 연산)
N이 3으로 나누어 떨어지진 않으니 N/3은 검증하지 않아도 된다.

이렇게 3가지 경우의 수를 검증하면 또 다시 가장 작은 연산횟수를 쌓아나갈 수 있는 것이다.

시간복잡도는 대략 O(N)이 나오게 된다.

let solution = (n) => {
  let d = [];

  d[0] = 0;
  d[1] = 0;

  for (let i = 2; i <= n; i++) {
    d[i] = d[i - 1] + 1;

    if (i % 3 === 0) {
      d[i] = Math.min(d[i], d[i / 3] + 1);
    }
    
    if (i % 2 === 0) {
      d[i] = Math.min(d[i], d[i / 2] + 1);
    }
  }

  return d[n];
};

const readline = require('readline');
const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

rl.on('line', function (line) {
  console.log(solution(+line));
  rl.close();
}).on('close', function () {
  process.exit();
});

2xn 타일링 (boj 11726)

문제 링크

• 2xn 직사각형을 1x2, 2x1 타일로 채우는 방법의 수

이 문제를 푸는 핵심은 역시 규칙성을 찾는 것이다.

간단히 이 문제에서 n의 증가와 타일을 채우는 방법의 수의 규칙성을 설명한 것은 아래와 같다.

• n=1일 때는 2x1 이므로 강제로 방법이 1가지밖에 없다.
• n=2일 때는 2x2 이므로 방법이 2가지밖에 없다.
• n=3일 때는 2x3인데 여기서부터 중요하다.
  • n=1일 때에서 = (세로 두개의 블럭)을 추가하는 경우의 수
  • n=2일 때에서 | (가로 하나의 블럭)을 추가하는 경우의 수

경우의 수가 계속 위와 같이 늘어난다.

결국 d[1]과 d[2]를 구하고 계속 d[n]=d[n-1]+d[n-2]를 하면 된다.

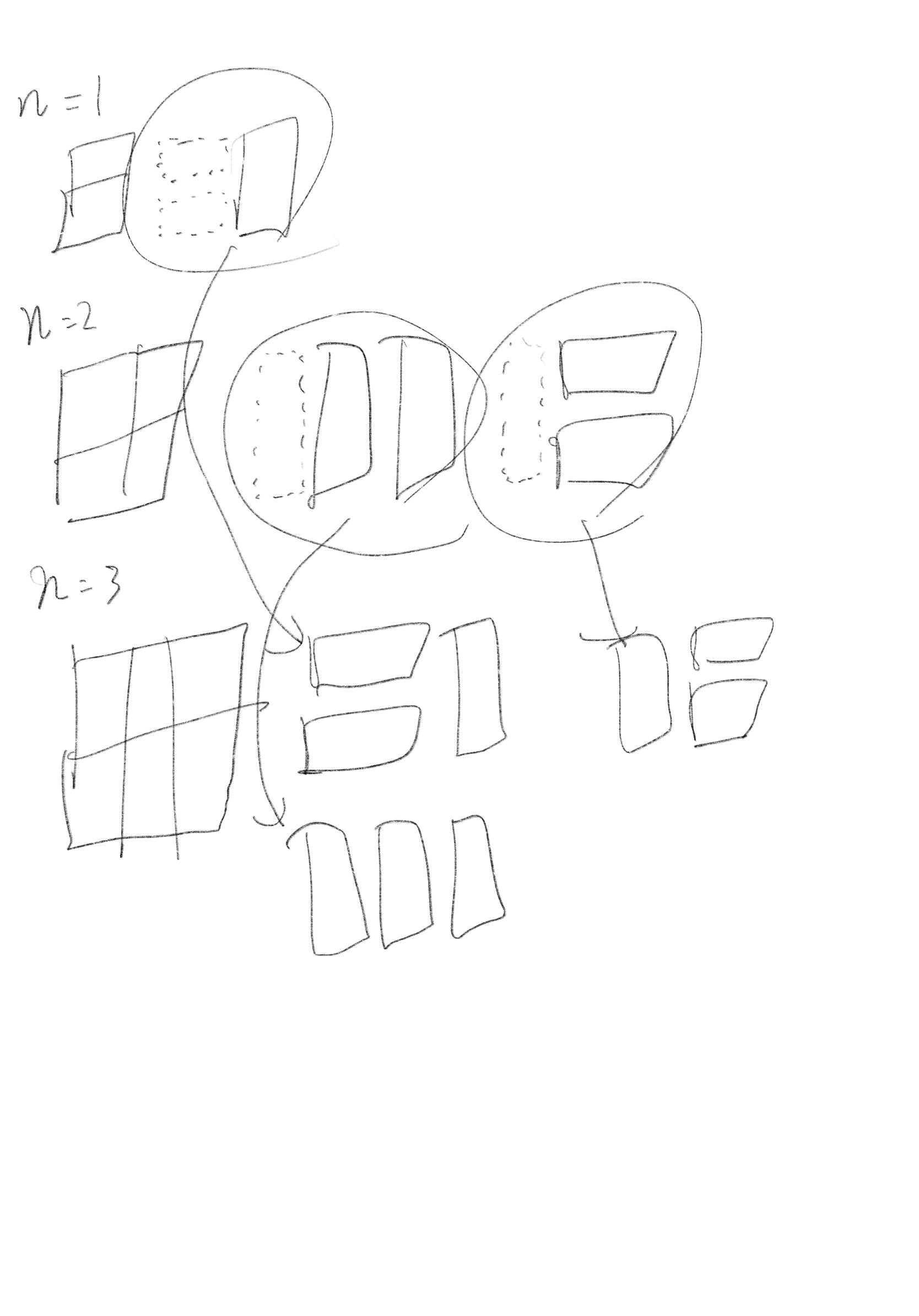
코드에서는 위의 규칙성에 + 매번 10007을 나눈 나머지를 반환하면 된다.

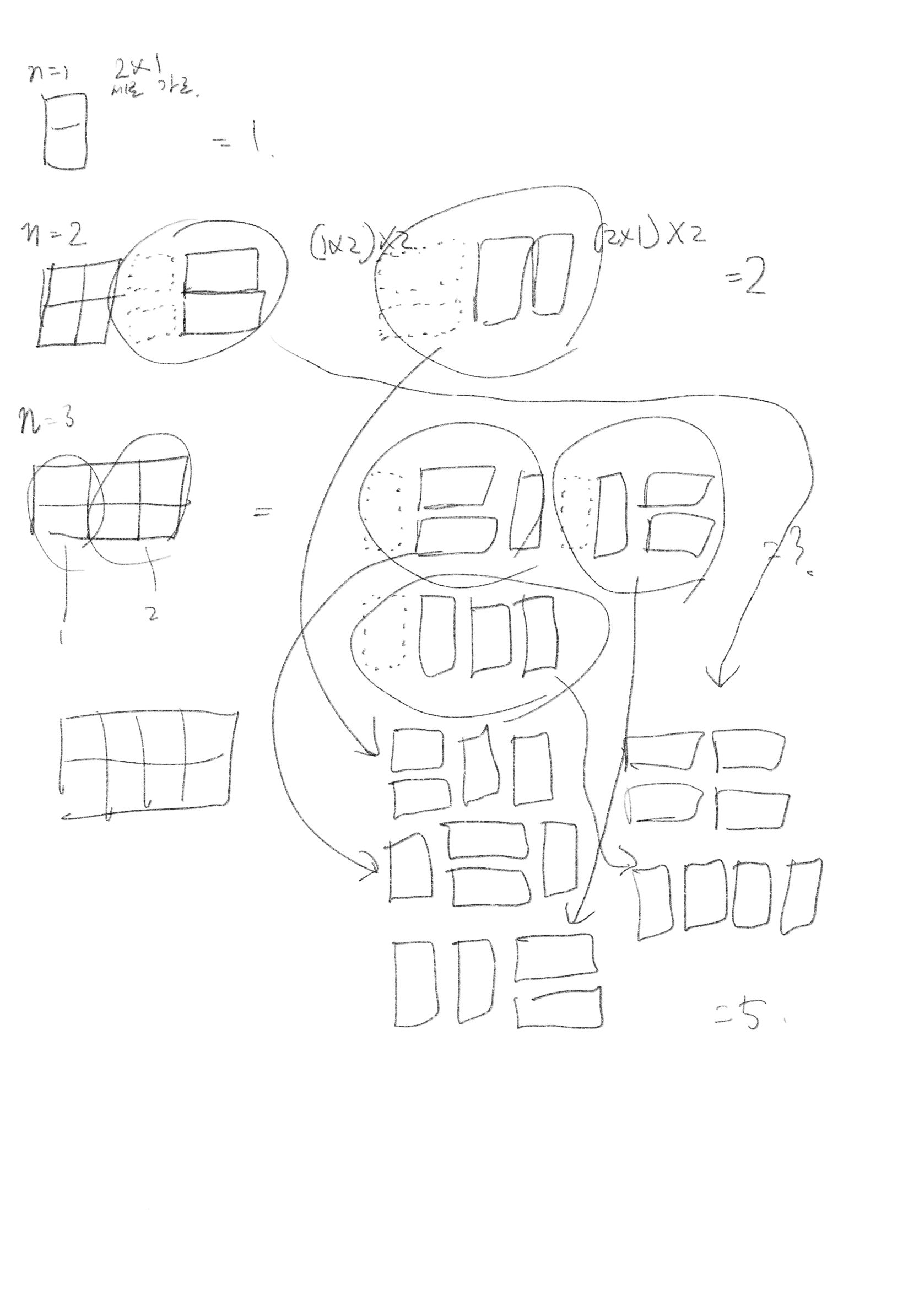
규칙성을 찾기 위한 분석은

위와 같이 하면 된다.

계속 반복되는 한 단계에서 추가되는 블록이 어떻게 형성되는지를 잘 살피면 된다. n이 아무리 늘어나도 블록은 저런 형태로만 늘어날 수 있다.

그럼 각각 |모양 블럭이 왔을 때 d[n-1]만큼 횟수가 늘어나고 =모양 블럭이 왔을 때, d[n-2]만큼 횟수가 늘어난다는 것을 알 수 있다.

let solution = (n) => {
  let d = new Array(n + 1).fill(0);

  d[1] = 1;
  d[2] = 2;

  for (let i = 3; i <= n; i++) {
    d[i] = (d[i - 1] + d[i - 2]) % 10007;
  }

  return d[n];
};

const readline = require('readline');
const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

rl.on('line', function (line) {
  console.log(solution(+line));
  rl.close();
}).on('close', function () {
  process.exit();
});

2xn 타일링 2 (boj 11727)

문제 링크

이 문제는 이전에 2xn 타일링 문제에서 아주 약간 변형된 건데, 도형을 그리면서 다시 생각해보면 쉽다.

n=1, n=2, n=3일 때의 경우의 수다

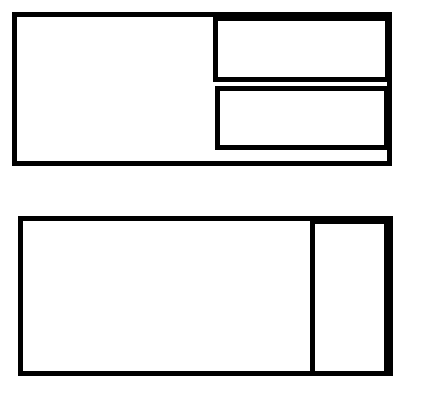
이걸 기준으로 n=4일때를 구해보면... n=4라는 것은 n=3에서 오른쪽에 2x1칸이 더 생긴것과 같다. 그래서 아래와 같은 경우의 수를 생각해볼 수 있다. 아래는 n=3일 때에 오른쪽에 막대기를 하나 더한 것이다.

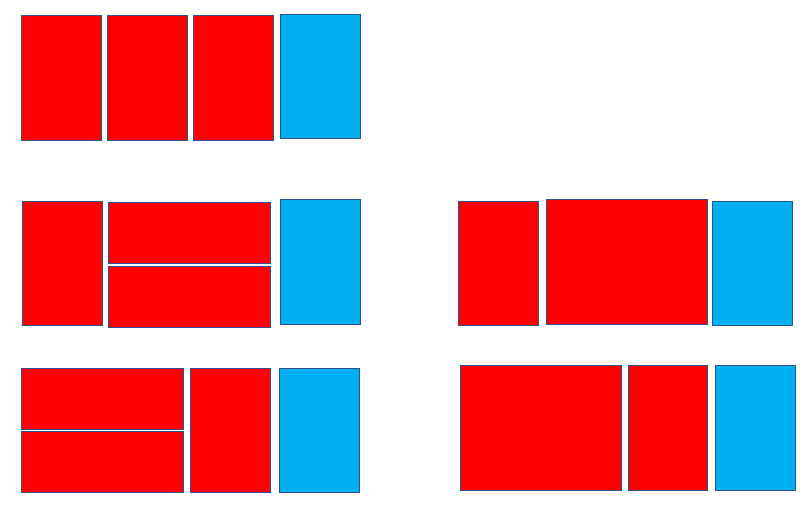
또한 n=4라는 것은 n=2에서 오른쪽에 2x2칸이 더 생긴것과도 같다. 그래서 아래와 같은 경우의 수도 생각해볼 수 있는데, 단, ||가 온 경우에는 n=3을 확장한 것과 중복되기 때문에 해당되지 않는다.

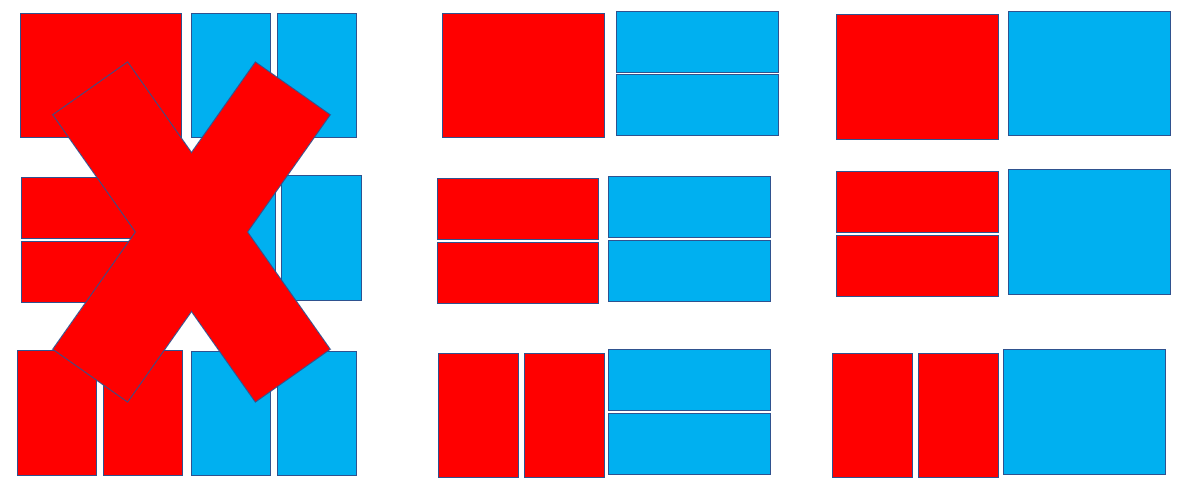
그래서 결국 n의 횟수를 구할 때 n-1 횟수 + n-2 횟수 * 2로 누적시켜 구하면 된다.

let solution = (n) => {
  let d = new Array(n + 1).fill(0);

  d[1] = 1;
  d[2] = 3;

  for (let i = 3; i <= n; i++) {
    d[i] = (d[i - 1] + d[i - 2] * 2) % 10007;
  }

  return d[n];
};

const readline = require('readline');
const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

rl.on('line', function (line) {
  console.log(solution(+line));
  rl.close();
}).on('close', function () {
  process.exit();
});

1, 2, 3 더하기

문제 링크

이 문제도 점화식을 잘 세우면 풀 수 있는데 점화식의 힌트는

N-1의 경우의 수에 +1을 하면 N이 되고
N-2의 경우의 수에 +2를 하면 N이 되고
N-3의 경우의 수에 +3을 하면 N이 된다는 것이다.

이렇게 대충 써보면서 알아보면 금방 식을 세울 수 있다.

let solution = (numbers) => {
  let d = new Array(10 + 1).fill(0);
  let answer = '';

  d[1] = 1;
  d[2] = 2;
  d[3] = 4;

  for (let i = 4; i <= 10; i++) {
    d[i] = d[i - 1] + d[i - 2] + d[i - 3];
  }

  for (let i = 1; i < numbers.length; i++) {
    answer += d[numbers[i]] + '\n';
  }

  return answer;
};

const readline = require('readline');
const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

let input = [];

rl.on('line', function (line) {
  input.push(line);
}).on('close', function () {
  console.log(solution(input));
  process.exit();
});

복잡도는 O(N)이다.