MPC (Secure Multi-Party Computation ) 이해하기 -2 / 2

이어서 해설을 완성한다.

Oblivious Transfer - 분실 통신

암호학적 2자 간 프로토콜로, 수신자가 송신자의 입력 중 하나를 비밀스럽게 선택할 수 있도록 한다. 이 프로토콜의 프라이버시 보장은 송신자는 수신자가 선택한 값을 알 수 없으며, 수신자는 선택하지 않은 입력 값을 알 수 없게 한다.

기본 예제: 1-out-of-2 둘 중 하나 OT

이 프로토콜에서는 송신자가 두 개의 메시지 $m0$ 와 $m1$을 가지고 있다. 수신자는 이 두 메시지 중 하나, 즉 $mb$ 를 알고 싶어하지만, 송신자 쪽에서 무엇이 선택되었는지 알 수 없게 하고자 한다.

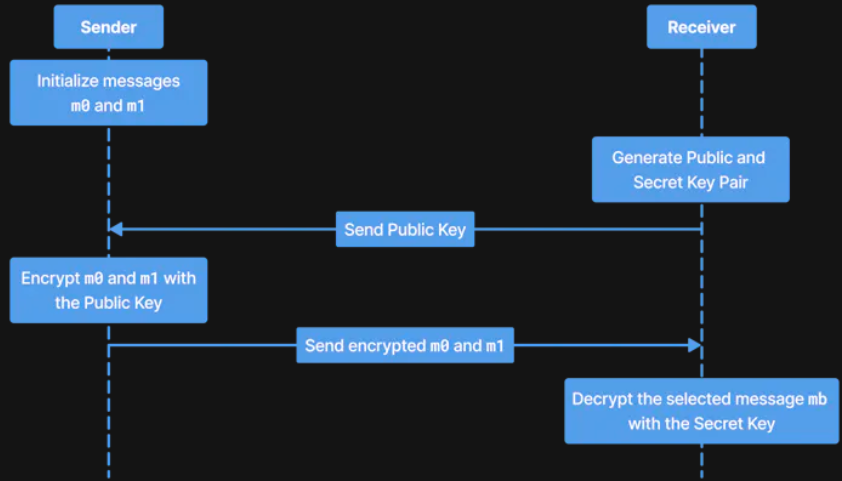
• 초기화

  • 송신자 (Sender) : 두 개의 메시지 $m0$ 와 $m1$ 을 보유.
  • 수신자 (Receiver) : 수신자는 메시지 중 하나를 선택하고자 한다. 인덱스는 b 이며, $b \in \{0,1\}$.

• 통신과정 :

  • 수신자는 공개키, 비밀키를 생성한다 (Public Key : $pk$ , Secret Key : $sk$)
  • 수신자는 송신자에게 $pk$를 보낸다.
  • 송신자는 $m0$, $m1$을 암호화 한다. 이떄 $pk$ 를 사용한다. 또 수신자의 $sk$ 는 한번만 쓸 수 있도록 설정한다. (선택된 메세지만 해독할 수 있도록 함)

• 전달 : 송신자는 암호화 된 메세지를 수신자에게 전달한다. 수신자는 $sk$를 이용해 복호화, 해독하며 $mb$ 를 선정한다. (즉, 0,1 둘 중 어느 것이 선정 되었는지 모르나, $mb$ 로 그것이 결정 되었다)

• 이 방식이라면 데이터의 프라이버시가 유지된다. 즉 수신자는 자신이 선택한 하나의 메세지 이외에 다른 메세지 내용은 알지 못한다. 송신자는 수신자가 어느 메세지를 선택했는지 알지 못한다.

암호화된 써킷 (Garbled Circuit)

Garbled Circuits (GCs) 은 1980년대에 Andrew Yao에 의해 소개된 안전한 2자 간 계산(2PC) 기술이다. GC 프로토콜은 가블러(Garbler) 와 평가자(Evaluator) 두 당사자가 협력하여 불리언 회로로 표현된 함수를 안전하게 평가하는 방식이다. 이 함수는 AND와 XOR 게이트로 구성되며, 각 당사자는 입력의 일부를 제공한다.

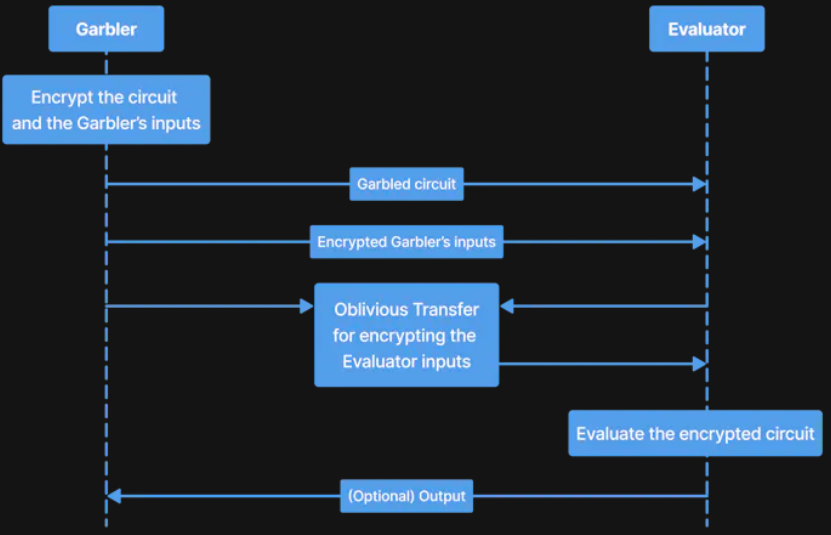
Circuit 써킷

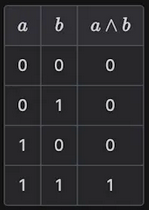
AND 게이트로 이루어진 간단한 써킷이다.

Garbling 암호화

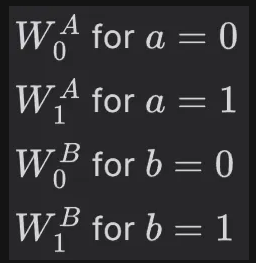
Garbler는 네개의 랜덤 String을 고른다. labels (레이블)이라고도 한다. Garbling은 진짜 (위의) 테이블을 숨기는 과정이다.

그리고 Garbler는 4개 레이블 모두를 이용해서 암호화된 아웃풋 테이블을 만든다.

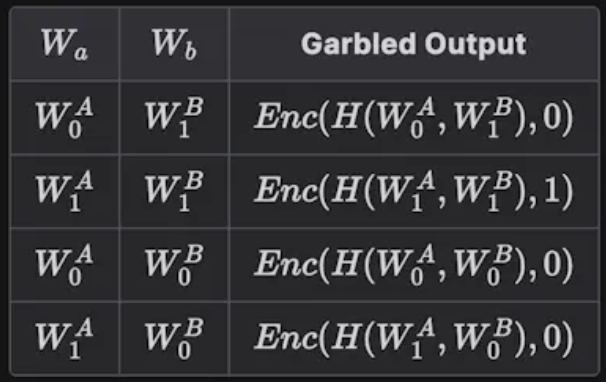
이후 순서를 랜덤으로 섞는다.

Evaluation 검토

어떤 검토자가 암호화된 게이트를 수신하면, 오로지 하나의 암호문을 해독해야 한다. 그것도 실제 a,b 값에 상응하는 실제 값으로.

따라서 Garbler에게 $W_{a}^A$, $W_{b}^B$ 대한 정보를 받는다.
Garbler는 a 값을 알고 있으므로 검토자에게 $W_{a}^A$ 값을 전달한다. 모든 레이블은 랜덤이므로 검토자는 a에 대한 정보를 알 수 없다.
하지만, $W_{b}^B$ 정보는 더욱 공개가 어렵다. Garbler는 $W_{0}^B$ , $W_{1}^B$ 모두 검토자에게 전달할 수 없다. 그렇게 되면 게이트 내의 두개 암호문에 대한 해독이 가능하다. 또한, 검토자도 마찬가지로 b에 대한 정보를 공개하고 싶지 않기 때문에 원하는 것을 요청할 수 없다.

여기서 Garbler와 검토자는 OT (Oblivious Transfer)를 실행한다. 이렇게 되면 검토자는 $W_{b}^B$에 대한 정보만 (b에 대해서는 여전히 숨긴 채로) 전달할 수 있다.

Garbling 예시

1. 초기화
   1. Garbler는 입력값 a와 b를 위한 레이블을 생성
   2. Garbler는 써킷을 생성 후 전송
2. 입력 레이블 분배
   1. Garbler는 $W_{0}^A$ 값을 검토자에게 전송 (a = 0 이므로)
3. OT 실행
   1. 검토자는 OT를 이용하여 $(W_{1})^B$ 를 수신한다 (b = 1 이므로)
4. 검토 실행
   1. 검토자는 확보한 Key $W_{0}^A$ 와 $W_{1}^B$ 를 가지고 테이블 내에서 복호화를 시도
   2. $Enc(H(W_{0}^a,W_{1}^B),W_{0}^{out}) \rightarrow W_{0}^{out}$
5. 결과 복원
   1. 검토자는 $W_{0}^{out}$ 키를 복호화 한 후 결과값을 0으로 매핑한다.

Secret Sharing

Secret sharing는 비밀 값을 분산하여 각 조각이 개별적으로는 비밀에 대한 정보를 드러내지 않도록 하는 방법이다. 비밀 값은 모든 조각 또는 충분한 수의 조각이 결합되어야만 복원할 수 있다.

Additive Secret Sharing의 작동 방식에 대해 살펴보자. 여기서는 3명의 참여자와 덧셈 연산을 예로 든다. 이 방식에서 비밀은 $m$개의 조각으로 나누어지고, 이 조각들을 모두 결합해야만 비밀을 복원할 수 있다.

결론:

비밀값 나누기 및 연산을 통해, 비밀 공유 숫자에 대한 연산을 수행할 수 있으며, 이 숫자들은 연속적으로 더 복잡한 함수로 처리할 수 있다. 이 방법을 통해, 주어진 회로에 따라 비밀 공유 숫자를 기반으로 계산을 수행할 수 있다:

• 당사자들의 비밀 입력은 비밀 공유 방식으로 나누어진다.
• 회로는 비밀 공유 숫자를 사용하여 게이트별로 평가된다.
• 최종 공유 결과로부터 출력이 재구성된다.

재구성은 마지막에만 발생하며, 모든 이전 단계에서는 당사자들이 자신의 공유된 조각으로 작업하여 비밀 입력에 대한 정보를 드러내지 않도록 한다.

1. 비밀값 나누기

단계	작업	계산식	결과
비밀값 선택	비밀값 $S$ 선택	$S = 1337$	1337
조각 선택	$m - 1$개의 랜덤 숫자 선택	$S_1 = 220$, $S_2 = 540$	220, 540
최종 조각 계산	최종 조각 $S_3$ 계산	$S_3 = S - (S_1 + S_2)$	577

2. 비밀값 나누기 예제

단계	작업	계산식	결과
비밀값 선택	비밀값 $T$ 선택	$T = 1440$	1440
조각 선택	조각 선택	$T_1 = 118$, $T_2 = 330$, $T_3 = 992$	118, 330, 992

3. 조각 분배

참가자	비밀값 $S$ 조각	비밀값 $T$ 조각
참가자 1	$S_1 = 220$	$T_1 = 118$
참가자 2	$S_2 = 540$	$T_2 = 330$
참가자 3	$S_3 = 577$	$T_3 = 992$

4. 연산 수행

참가자	덧셈 연산	계산식	결과
참가자 1	$S_1 + T_1$	$220 + 118$	338
참가자 2	$S_2 + T_2$	$540 + 330$	870
참가자 3	$S_3 + T_3$	$577 + 992$	1569

\

참가자	비밀값 $S$ 조각	비밀값 $T$ 조각	연산 결과	계산식	결과
참가자 1	$S_1 = 220$	$T_1 = 118$	$R_1$	$S_1 + T_1 = 220 + 118$	338
참가자 2	$S_2 = 540$	$T_2 = 330$	$R_2$	$S_2 + T_2 = 540 + 330$	870
참가자 3	$S_3 = 577$	$T_3 = 992$	$R_3$	$S_3 + T_3 = 577 + 992$	1569

5. 비밀값 재구성

단계	작업	계산식	결과
비밀값 재구성	최종 결과 계산	$R = (S_1 + S_2 + S_3) + (T_1 + T_2 + T_3)$	2777

MPC의 보안 및 성능

보안 측면의 함의

• 신뢰의 부재: MPC에서는 어느 한쪽 당사자도 절대적으로 신뢰 되지 않는다. 당사자들은 프로토콜을 통해 상호작용하며, 이 프로토콜은 각 참여자의 예상되는 행동과 통신의 범위를 정의한다. 프로토콜은 각 단계에서 수행할 작업, 즉 어떤 메시지를, 누구에게, 언제 보낼지 등을 지정한다.
• 적대자의 공격: 적대자는 프로세스의 어떤 단계에서든 참가자를 손상시킬 수 있다. 위협 모델에 따라 손상된 당사자는 프로토콜을 따르거나 떠나게 된다.
  • 반정직(Honest-but-curious): 이러한 적대자는 참가자를 손상시키지만 지정된 프로토콜을 따른다. 프로토콜을 정직하게 실행하면서도 다른 당사자로부터 받은 메시지에서 가능한 한 많은 정보를 취득하려고 한다.
  • 악의적(Active): 이러한 적대자는 손상된 당사자가 프로토콜에서 이탈하도록 유도한다.
• 보안성 보장: 보안 보장 측면에서 프로토콜을 다음과 같이 분류할 수 있다.
  • 정직한 다수의 존재에서 보안을 보장하는 프로토콜: 이러한 프로토콜은 일반적으로 두 번째 유형보다 효율적이다.
  • 임의의 수의 손상된 당사자에 대해 보안을 보장하는 프로토콜: 이러한 프로토콜은 당사자 간의 신뢰 없이도 보안을 제공하므로 중요한 이점을 제공한다. 특히 안전한 2자간 연산에서 중요합니다.

성능 고려사항

• 효율성 한계: 높은 MPC에 대한 수요에도 불구하고, 실용적 채택은 제한적이다다. 이는 프로토콜의 비효율성에 기반한다. 이론적으로 30년 이상 알려진 이러한 프로토콜은 대부분 실용적인 용도에는 너무 비효율적이다.
• 통신 및 연산: 성능에 영향을 미치는 두 가지 주요 요소는 통신과 연산이다.
  • 통신: 여기에는 교환되는 데이터의 양과 필요한 통신 (상호작용) 라운드 수가 포함된다.
    • 데이터 양: 프로토콜 실행 중 당사자 간에 교환되는 메시지의 총 크기
    • 통신 라운드: 프로토콜을 완료하는 데 필요한 메시지 교환의 횟수입니다.
  • 연산: 요구되는 연산처리 능력. 여기서 주요 요소는 복잡도와 암호화 연산의 수이다.
• 실행 시간: 아래 [1]의 결과에서 볼 수 있듯이 MPC는 제한된 참가자 수, 낮은 대기 지연 시간 및 높은 전송 속도를 가진 인트라넷 애플리케이션에 적합하다. 반면 덜 최적화된 조건에서는 실행 시간이 기하급수적으로 증가한다. 특히 다음과 같은 경우가 있습니다.
  • 전송 속도: 전송 속도가 낮으면 실행 시간이 현저하게 지연
  • 피어 수: 피어(참여자) 수가 증가하면 실행 시간또한 증가
  • 네트워크 지연 시간: 네트워크 대기 시간이 조금만 지연되어도 실행 시간이 크게 증가
• 실용성: 따라서 실시간 MPC 애플리케이션은 현재 실현 가능하지 않은 것으로 보이지만, 더 유연한 시간 제약이나 더 빠른 인프라를 사용하는 경우는 여전히 실행 가능합니다.

프로그래밍 된 암호학

MPC는 영지식 증명 (ZK) 및 완전 동형 암호화(FHE)와 통합되어 보안 및 기능성을 향상시킬 수 있다. PSE 블로그에서 다음 리소스를 참고하자

• Zero to Start: Applied Fully Homomorphic Encryption
• Beyond Zero-Knowledge: What’s Next in Programmable Cryptography?

결론

안전한 다자간 연산은 여러 당사자가 개인 데이터를 공개하지 않고 함수에 대해 함께 작업할 수 있도록 하는 강력한 암호화 도구이다. 높은 잠재력에도 불구하고 높은 통신 비용 및 집중적인 계산 요구와 같은 문제로 인해 실용적용이 매우 제한되었다. 그러나 기술이 발전하고 프로토콜이 개선됨에 따라 MPC 애플리케이션이 증가하고 있으며 이 기술은 점점 더 통합되는 디지털 세계에서 안전하고 분산된 계산 및 데이터 분석을 가능하게 하는 핵심이다.