Fri-Based STARK 스타크 기법의 핵심 Folding에 대하여

ZK-STARK

• FRI Based STARK

  1) Why Learn Stark? 왜 STARK에 주목해야 하는가?

  https://youtu.be/8bj1dWcMslY?si=DQDTLRgzkrakeQ5d
  

* Many advantages over KZG Based SNARK!

내 개인적인 의견으로는, STARK 방식이 더 발전 속도가 빠른 기술이다. 하드웨어는 지속적으로 발전하고, 가격은 낮아지는데, 이를 충분히 활용하는 방식이 STARK이기 때문이다. 물론 KZG의 장점인 Short Proof Size (~200 Bytes)도 인정하지만, 압도적인 하드웨어 성능 향상에 대비하면 체감 효과가 미미해진다. 반면 Stark는 모든 방식의 Trust Setup 을 지원하며, All Finite Field 를 커버한다. 이는 Verifying(검증)자에게 다양한 작업을 의존할 수 있으며 더 많은 Use Case를 이끌어낸다.

배경 지식 : Folding 이란?

https://medium.com/starkware/low-degree-testing-f7614f5172db
Splitting a polynomial into two smaller-degree polynomials

예를 들어 n차항을 최고 차수로 가지는 다항식이 있을때 (위의 $F(x)$ 함수)
$g(x)$ 와 $h(x)$ 로 나누어, 각각 짝수항, 홀수항을 배치 시킨다. 이후 홀수 항은 $x$ 이상의 차수로 이루어져 있으므로 $x$로 한번 묶어 내면 $x*h'(x)$ 로, $h'(x)$ 는 다시 모든 차 항이 짝수가 된다. 이후 $g(x)$ 와 $h'(x)$의 모든 항의 차수를 전반으로 줄인다.

여기서, Folding을 잘 설명한 예제가 Risc Zero 팀의 Paul Gafni 가 잘 설명했다. 이때 Splitting 과 Mixing으로 나누어 설명하는데, 이는 Paul의 개인적 설명 노하우다.

https://youtu.be/wqRuoyH3Mqk?si=0sFvAKwQg7mrjStH

이때 Mixxing 단계에서 Verifier 측의 Random 상수 (Scalar) 를 Challange 값으로 받게 되는데, 이는 흔히 볼 수 있는 증명방식이다. ('너 진짜야? 이거 넣어서도 할 수 있어?'방식)
또, 이것 또한 Fiat-Shamir 방식으로 Prover가 Random 값까지 모두 넣어 Proof를 생성하여 Verifier에게 전달하게 된다. 이 또한 흔항 증명 방식이다.

놀랍게도, 이것이 STARK 방식에서 손으로 풀어 따라가볼 수 있는 증명의 전부다. 나머지는 모두 논리의 전개이다.

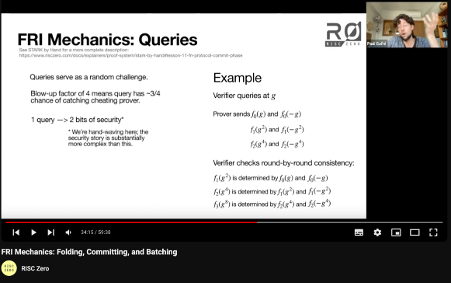
Queries : 이때 만들어지는 축약된 다항식(Polynomials)들과 - 예를 들어 16차를 8차로, 4차로, 2차로, 마지막에는 상수로 - 이 과정에서 개입된 Random 값들 (Verifier 가 던져 주기도 하고, 아니면 스스로 Random 함수를 사용할 수도 있는) 을 함께 제공한다. 이를 통해 Prover는 Polynomial을 완전히 알고 있다고 증명할 수 있다.
Safety : 이 과정에서 Folding 한번에 2 bits of security가 쓰인다고 위 영상에서는 설명한다. 0,1로 이루어진 bit 이니, 2 bits 는 4가지 경우의 수 이다. - 실제로는 정확하게 구해내려면 더 복잡하다고 한다. Folding 또한 16차를 한번에 줄인다. - 즉, $1/4$ 의 확률로 Malicious Prover는 Cheating이 가능 하다. 이게 Folding 한번이니, Folding 횟수가 늘어날 수록 Security가 증가한다. 실제 Starknet 에서는 96 bit 보안성을 제공하며 이는 $\left(\frac{1}{2}\right)^{96}$ 의 보안성을 뜻한다. 실제로는 이보다 훨씬 작다.
https://www.starknet.io/blog/safe-and-sound-a-deep-dive-into-stark-security/

https://starkware.co/stark-101/
위 링크에서는 Starkware 에서 제공하는 STARK 의 학문적, 기술적 기반을 교육한다.

https://youtu.be/gd1NbKUOJwA?si=T60xak67CBPvke2A

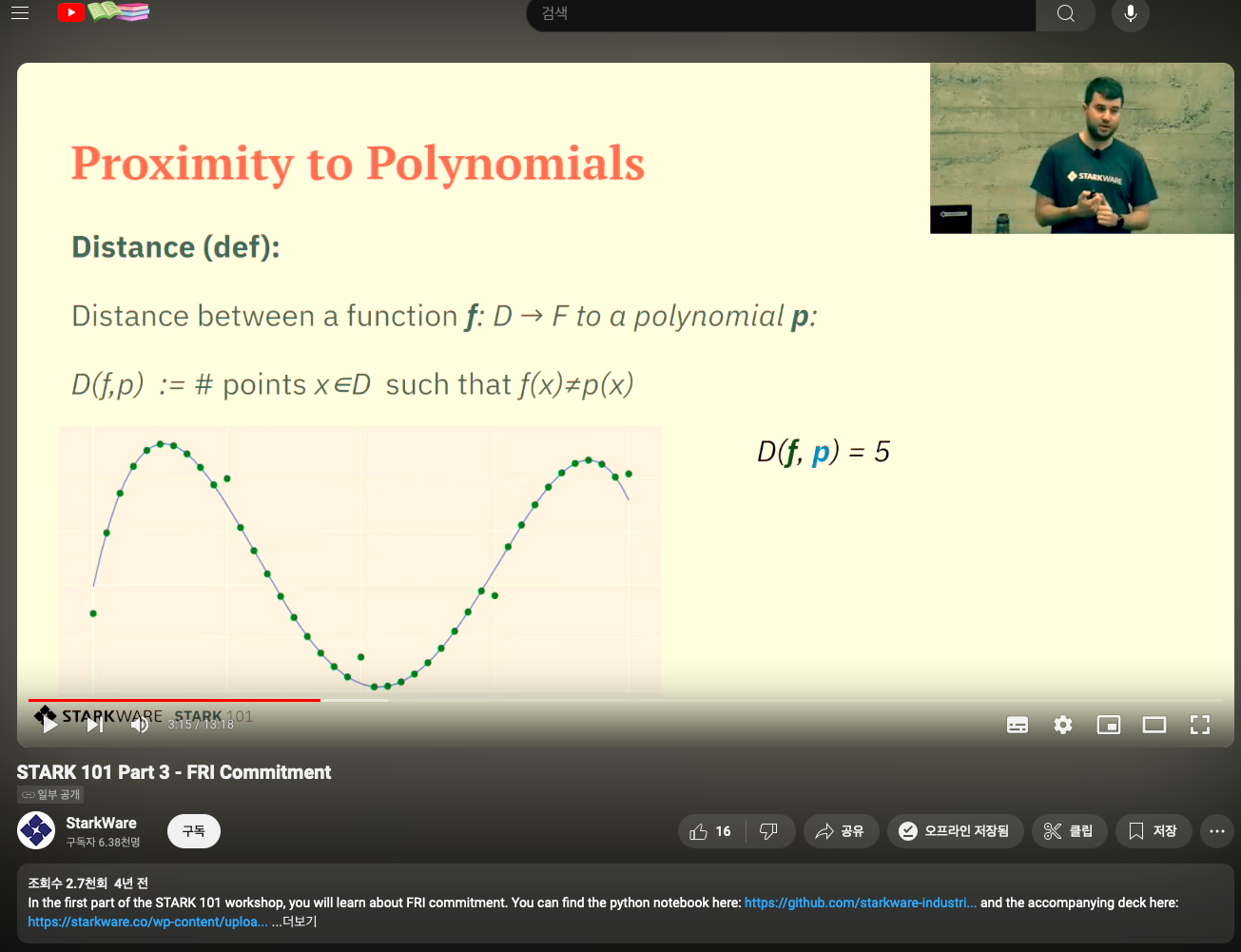
위 예를 들어 Part 3에서는 위와 같이 원본 Polynomial $P$와 주어진 점들로 근사해낸 Function $f$ 와 의 거리를 $D$로 나타내고, 이것이 "Small Enough" 해야 Safety가 보장되는 등으로 설명한다. 이를 위해 Reed-Solomon 예제를 잠시 들면,

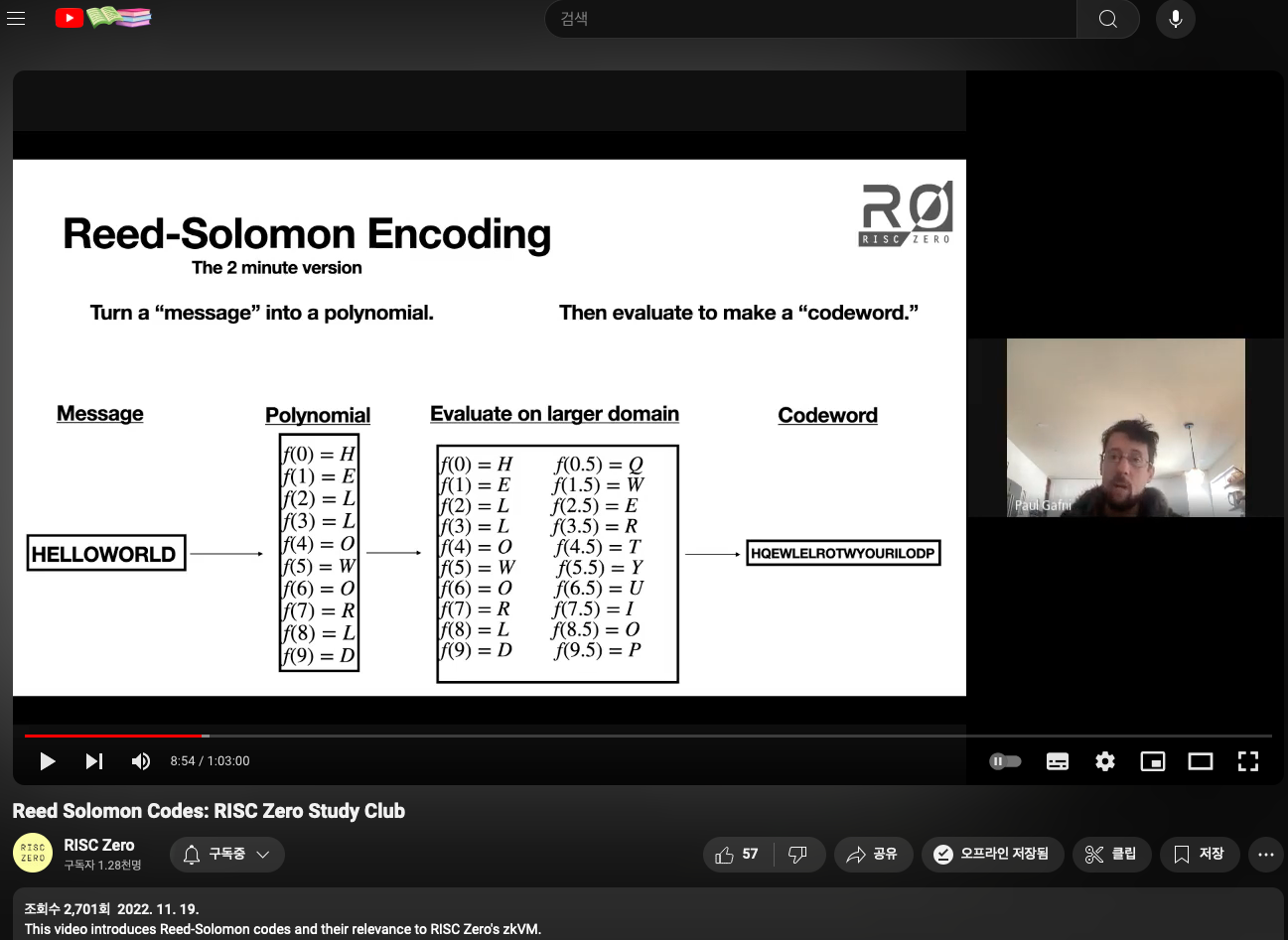
예를 들어, Alice 와 Bob이 송/수신을 하는 Channel이 있다고 가정하자. 이때 손실률이 50%이다. Alice가 Hello World를 송신하면 수신하는 Bob은 그 절반밖에 받지 못하는 것이다. 따라서 송신측은 Hello World를 지나는 Polynomial을 만들고, H 와 e 사이에 한번, e와 l 사이에 한번, 이런식으로 점을 찍어 총 2배의 점을 만들어 제공한다. 이 과정을 통해 Polinomial을 지나는 점을 2배로 뻥튀기 하여 송신하면, 수신 측에서는 50%의 손실이 발생하더라도 원본 Polynomail을 근사해낼 수 있다. 이것이 Reed-Solomon 기법의 핵심이다.

물론 이 Reed-Solomon 은 기법의 토대가 될 뿐 직접 기반이 되는 것은 아니다. Bob 입장에서 20개의 점을 부여 받고, Polynomial을 근사 해 보았는데, 실제 차수가 4차가 나오게 되면, 보내는 측의 정합성을 높은 확률로 추정해 낼 수 있다는 것이 핵심이다.

실제 동기들에게 Stark 방식의 보안 방식을 설명해보고, 토론해보니 느낀점이 있다. 이 "높은 확률"로 추정해 낸 다는 것이 받아들이기 어려운 듯 하다. 실제로 Groth16 을 공부하며 R1CS-QAP 등으로 식을 전개 해 나가면, Polynomial을 축약하거나, 빠르게 연산하는 방법으로 접근하여 "근사해 낸다"는 개념이 개입되지 않는다. 정합성을 추정하면, 어떻게 100% 안전하다고 할 수 있겠는가? 라는 궁금증이 드는 듯 하다. 향후 추가 포스트를 통해, 이 부분에 집중하여 설명하겠다. 다만 결론은, Quantum Secure 한 쪽은 오히려 STARK 이다.

이번 글에서는 FRI Method에 핵심이 되는 개념과 정리를 살펴 봤다. 현재는 STWO라고 하여 Starknet의 두번째 Proving System이 나왔는데, 기존보다 빠르고 효율적이라고 한다. 이바닥은 변화가 빨라 다음에 또 한번 정리 하겠다.

현재 STARK 진영에서 두각을 나타내고 있는 팀은 Starkware, Risc Zero, Succint Labs, Aligned가 있다. 모두 자체적인 기술력을 갖고 있으며 경쟁중이다. 현재까지는 Starkware가 선두로 여겨진다. 기술 경쟁 전에, 교육경쟁도 좀 해줬으면 좋겠다.