세그먼트 트리란 (feat. 완전 탐색, 누적합)

비구름·2024년 10월 16일

자료구조

목록 보기

1/6

세그먼트 트리란?

자식노드의 특성을 부모노드에 두는 것으로 한 배열에서 여러 구간의 최댓값, 최솟값, 합등을 구할 때 사용되는 것으로 전체를 탐색하는 시간보다 시간복잡도를 줄일 수 있습니다. 또한 누적합과는 다르게 배열의 요소 중 일부를 수정하더라도 사용할 수 있습니다.

문제 상황

간단한 문제에서 업그레이드하며 새로운 알고리즘을 넣어 진행하도록 하겠습니다.

완전 탐색

위와 같은 배열이 있고 사용자가 입력한 구간의 합을 구하시오. 단지 이렇게만 되어있으면 해당 구간을 조회하면서 구하면 간단하게 해결이 가능합니다.

public static void main(String[] args) throws IOException {
    var arr = new int[]{1, 2, 3, 4, 5, 6, 7, 8};

    var result = 0;
    var bf = new BufferedReader(new InputStreamReader(System.in));
    var range = Arrays.stream(bf.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();

    for (int i=range[0]; i<=range[1]; i++) {
        result += arr[i];
    }

    System.out.println(result);
}

각 배열의 위치를 탐색하며 직접 더해가는 방식입니다. 시간 복잡도는 $O(N)$ 으로 굉장히 양호한 시간입니다.

하지만 구간의 입력이 한번이 아닌 여러번 탐색하면 어떻게 될까요?

public static void main(String[] args) throws IOException {
    var arr = new int[]{1, 2, 3, 4, 5, 6, 7, 8};

    var bf = new BufferedReader(new InputStreamReader(System.in));
    var T = Integer.parseInt(bf.readLine());
    for (int t=0; t<T; t++) {
        var result = 0;

        var range = Arrays.stream(bf.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();

        for (int i = range[0]; i <= range[1]; i++) {
            result += arr[i];
        }
        System.out.println(result);
    }

}

시간 복잡도는 $O(TN)$ 으로 배열의 크기가 커질수록 시간 복잡도는 커집니다. 또한 탐색 과정에서 같은 구간을 반복해서 탐색하므로 비효율적인 방법이 되며 보통 이러한 상황을 해결하기 위해 보통 누적합이라는 것을 사용하게 됩니다.

누적합

누적합은 처음부터 해당 인덱스까지의 합을 배열로 저장시킨 것이며 모든 인덱스의 탐색이 아닌 인덱스 탐색을 2번으로 줄여 $O(1)$ 로 굉장히 빠르게 구할 수 있습니다.

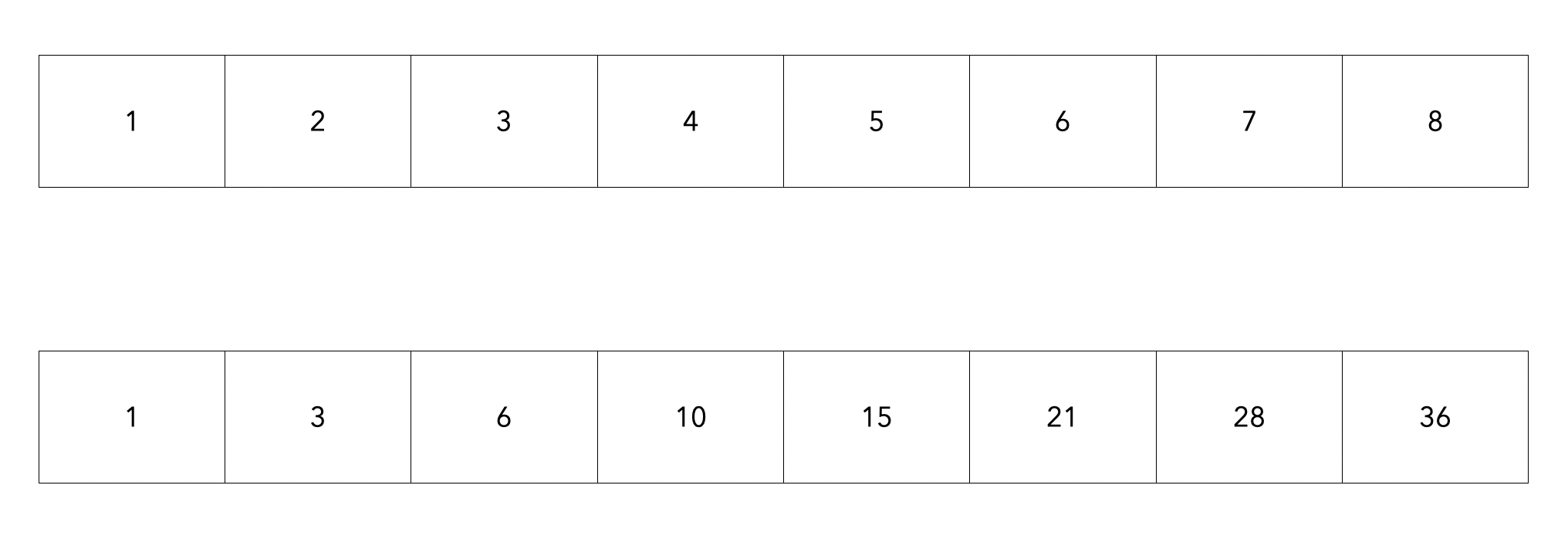
위의 배열이 기존의 배열이며 아래의 배열이 누적합을 이용한 배열입니다.

누적합의 배열은 다음과 같이 구성됩니다.

sum[i] = i==0?arr[i]:arr[i]+sum[i-1];

다음과 같이 쉽게 구성할 수 있으며 [a, b]구간의 범위를 구하려면 sum[b] - sum[a-1]로 구하면 빠르게 해결됩니다.

전체코드는 다음과 같습니다.

public static void main(String[] args) throws IOException {
    var arr = new int[]{1, 2, 3, 4, 5, 6, 7, 8};

    var sum = new int[arr.length];

    sum[0] = arr[0];

    for (int i=1; i<arr.length; i++) {
        sum[i] = sum[i-1] + arr[i];
    }

    var bf = new BufferedReader(new InputStreamReader(System.in));
    var T = Integer.parseInt(bf.readLine());
    for (int t=0; t<T; t++) {
        var range = Arrays.stream(bf.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();

        var result = sum[range[1]] - (range[0]==0?0:sum[range[0]-1]);

        System.out.println(result);
    }
}

하지만 배열의 값이 일부가 수정된다면 해당 누적합을 다시 구하기위해 수정될 때마다 $O(N)$ 이라는 시간복잡도를 가지게 됩니다. 따라서 배열의 수정이 자주 일어난다면 세그먼트 트리를 활용하는 것이 좋습니다.

세그먼트 트리로 탐색 및 수정

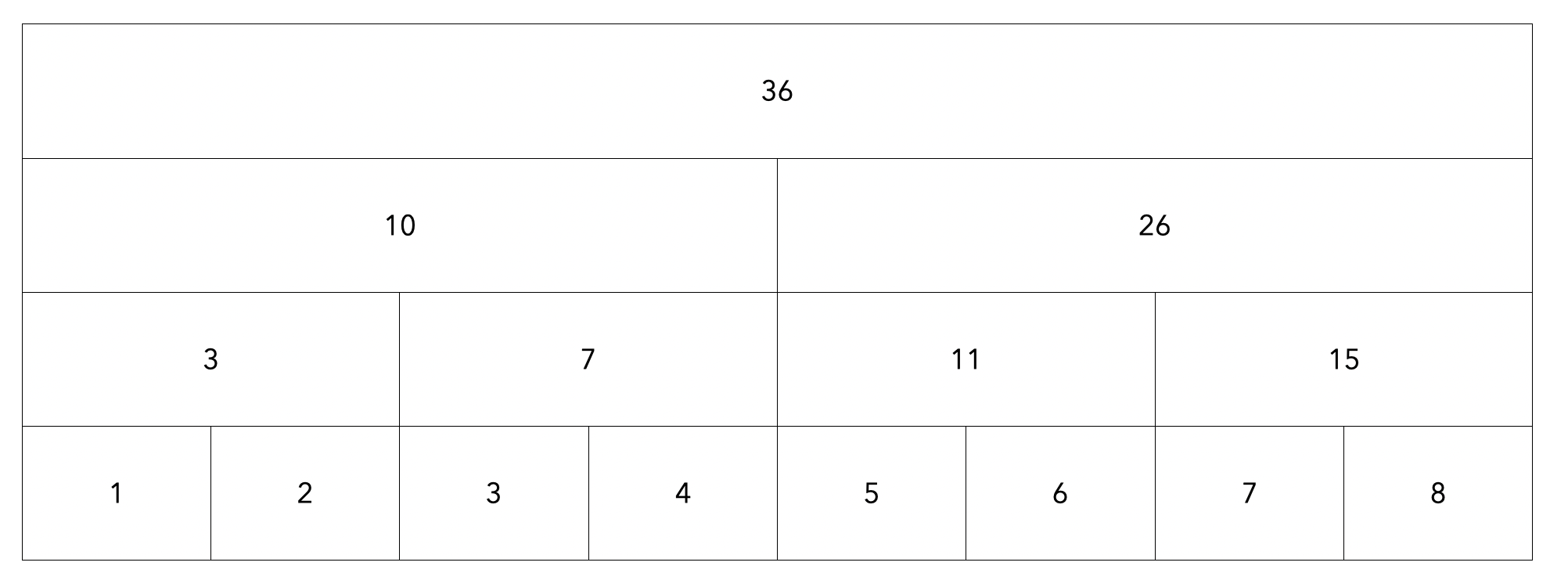
세그먼트 트리는 위와같이 구성됩니다. 가장 아래에 위치한 노드는 배열의 값과 동일하며 부모노드는 자식노드의 합을 가져 각 노드는 배열의 특정 구간의 합으로 구성되어 있습니다.

범위를 옆에 적어주면 다음과 같습니다

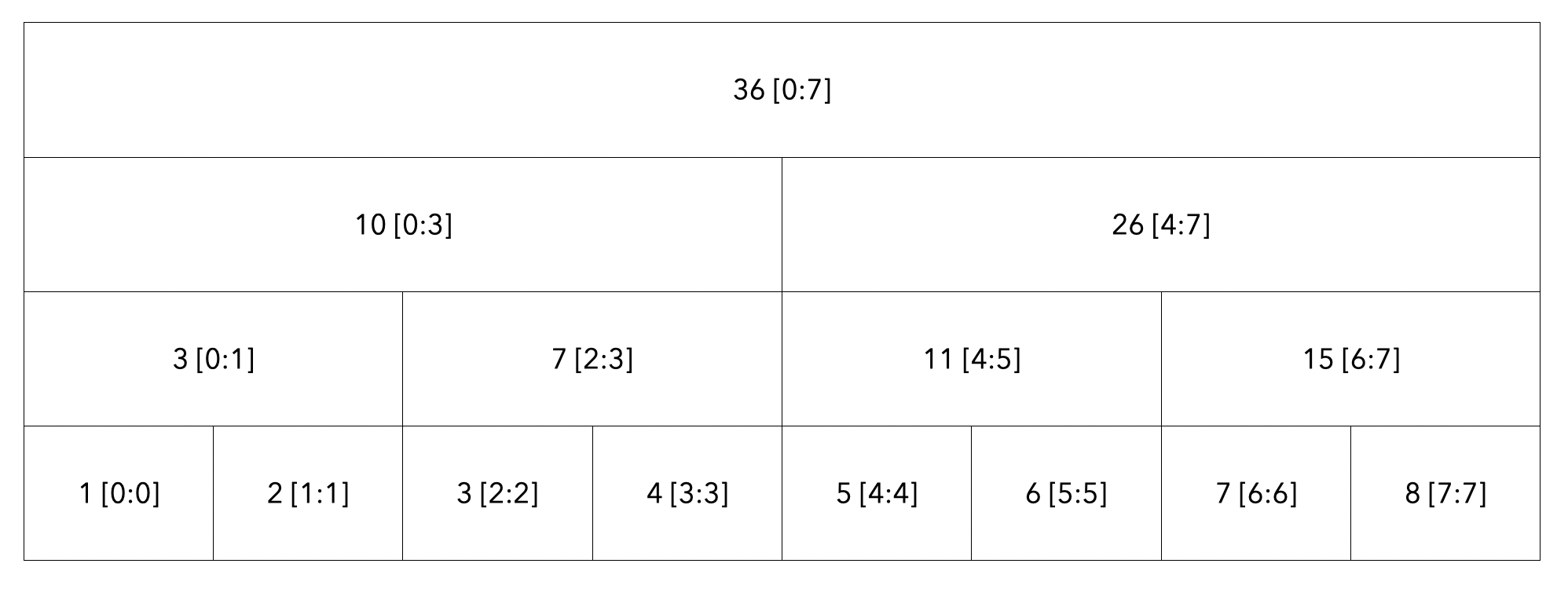
[2:5] 범위 탐색

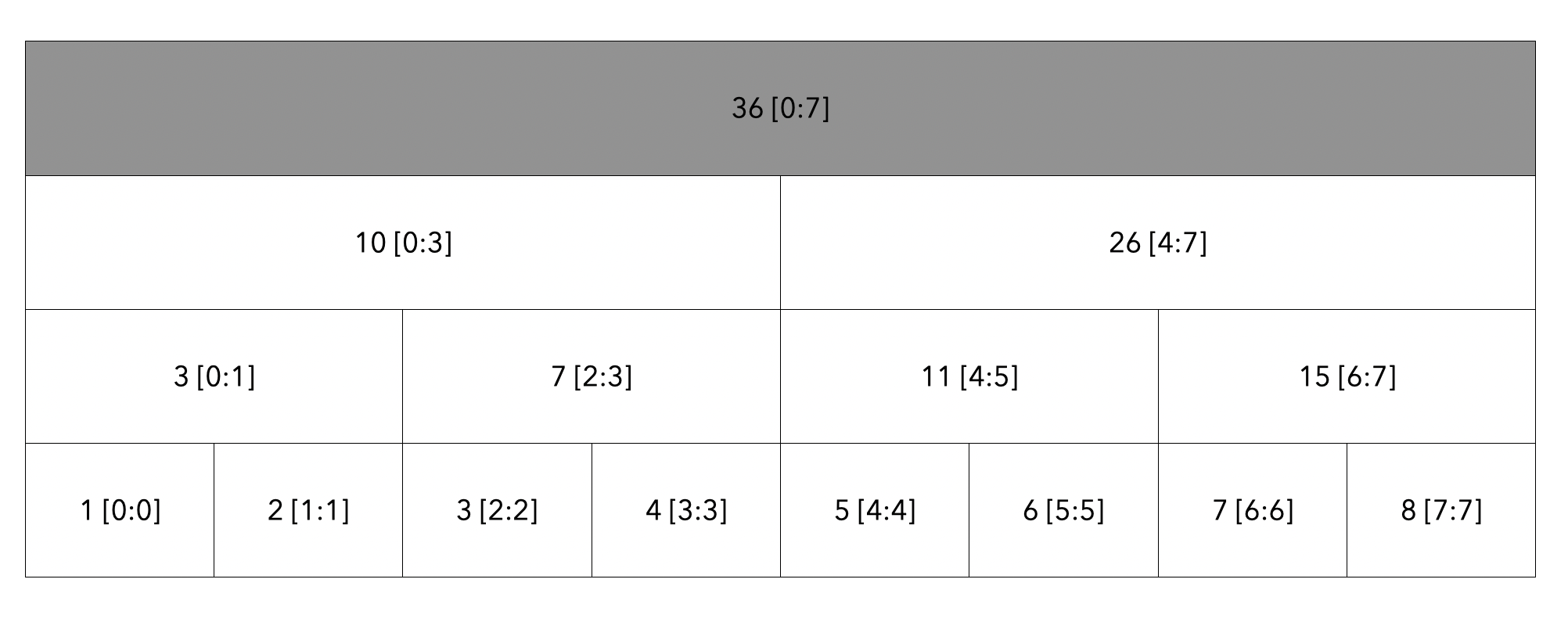
루트 노드부터 탐색합니다. 탐색할 범위는 [2:5]이고 현재 노드의 범위는 [0:7]이므로 자식 노드로 내려갑니다.

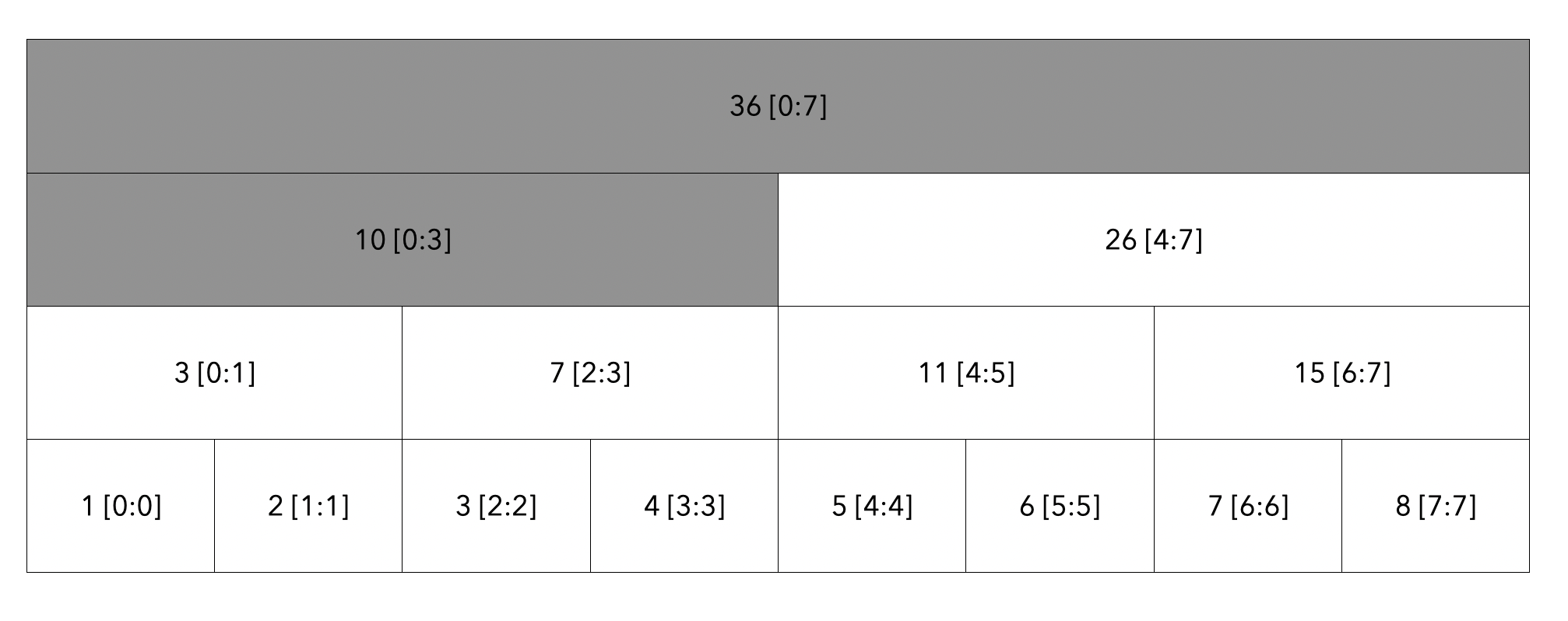
현재 노드의 범위는 [0:3]이며 탐색할 노드의 범위는 [2:5]이므로 자식노드로 내려갑니다.

좌측 자식 노드 범위인 [0:1]은 [2:5] 범위에 들어가지 않으므로 해당 구역의 탐색을 하지 않습니다. 하지만 우측 자식노드 범위인 [2:3]은 [2:5] 범위에 들어가므로 해당 노드 값인 7을 더해주게 되면서 루트노드에서 좌측 노드의 탐색을 마칩니다.

최종 탐색을 하면 다음과 같이 탐색이 됩니다.

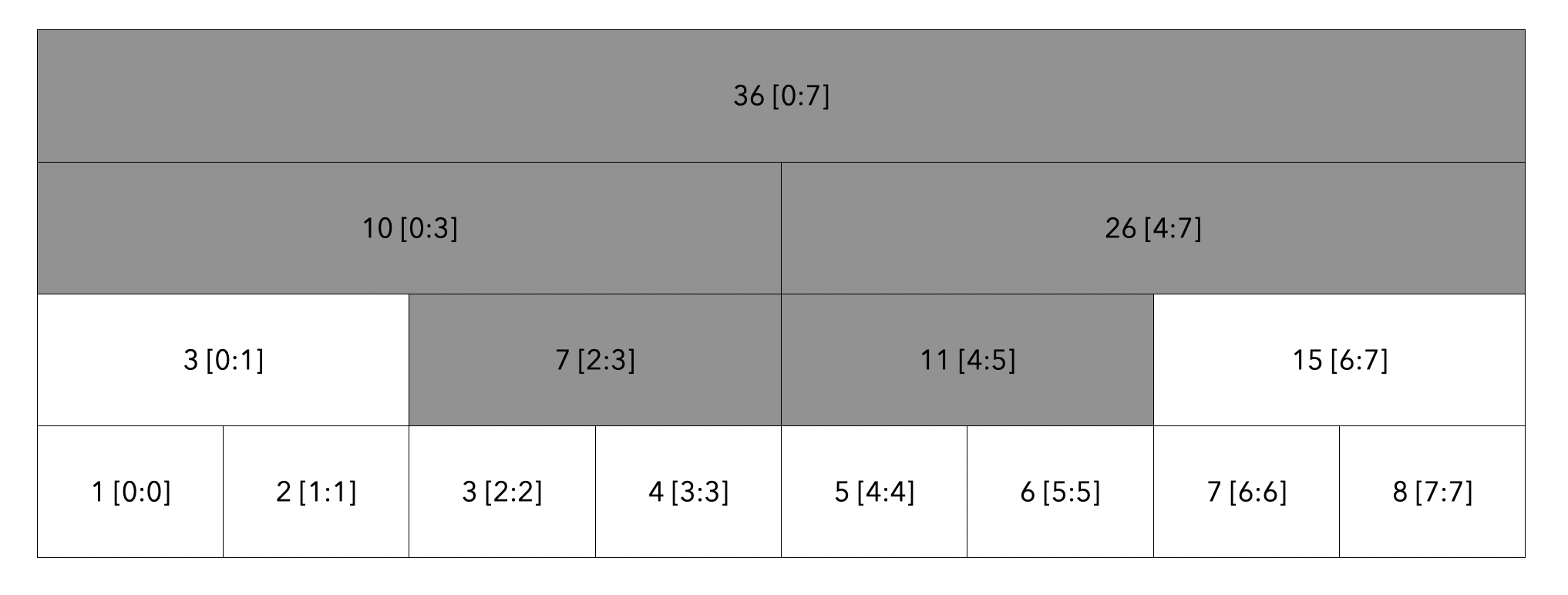
탐색한 모든 노드의 값인 7[2:3] + 11 [4:5]를 더하여 18이라는 결과를 도출하게 됩니다.

[0:4] 탐색

탐색한 모든 노드의 값인 10[0:3] + 5 [4:4]를 더하여 15라는 결과를 도출하게 됩니다.

탐색의 시간 복잡도

이진 트리로 구성된 세그먼트 트리는 각 레벨은 4개 이상 한번에 탐색하는 경우가 존재하지 않습니다. 탐색하는 모든 노드는 연속되어 구성되는데 [1:4] 범위를 탐색한다고 가정하면 2레벨에서 [0:1], [2:3], [4:5]가 같이 탐색이 되고 가장 높은 레벨의 3레벨에서 [1:1], [4:4]만 탐색하게 됩니다. 따라서 탐색의 시간은 $O(log_2N)$ 이 되며 누적합보다는 큰 시간복잡도를 가지게 됩니다.

3번 인덱스 7로 수정

누적합에 비해 세그먼트 트리가 가지는 장점은 바로 수정의 시간이 빠르다는 것입니다.

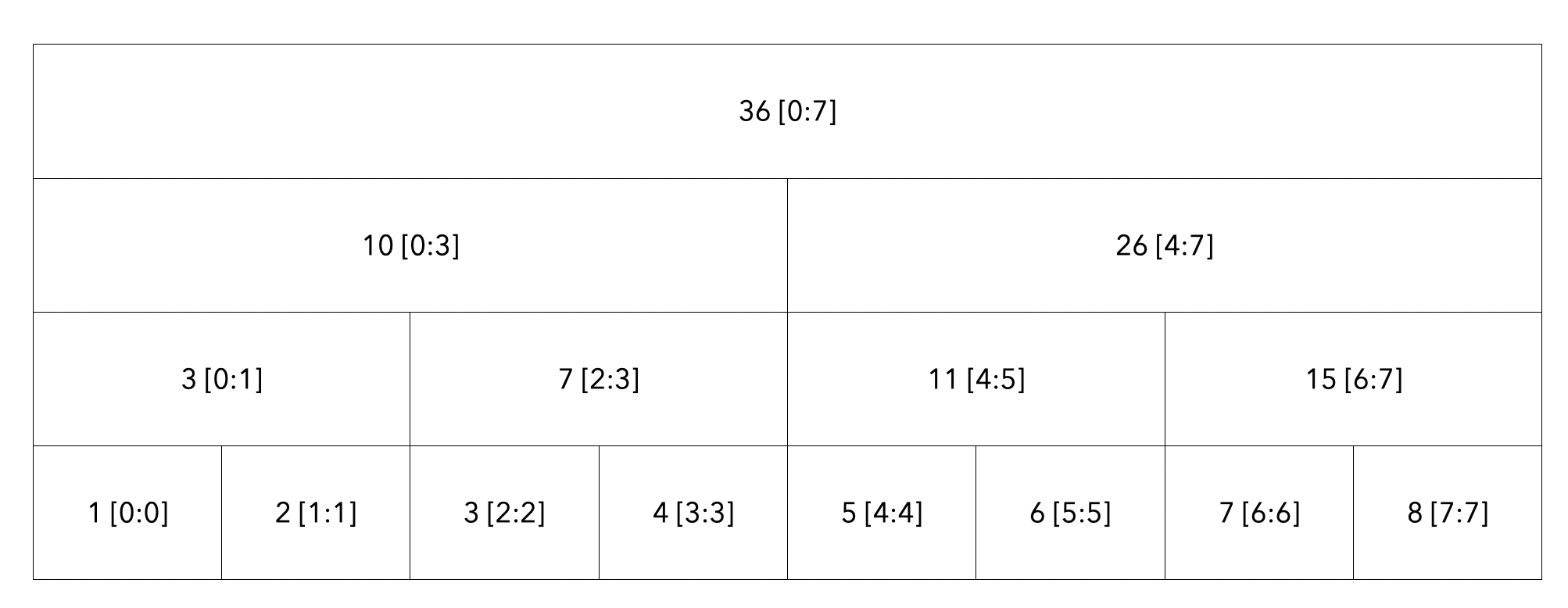
위의 누적합에서 3번 인덱스를 7로 변경해봅시다.

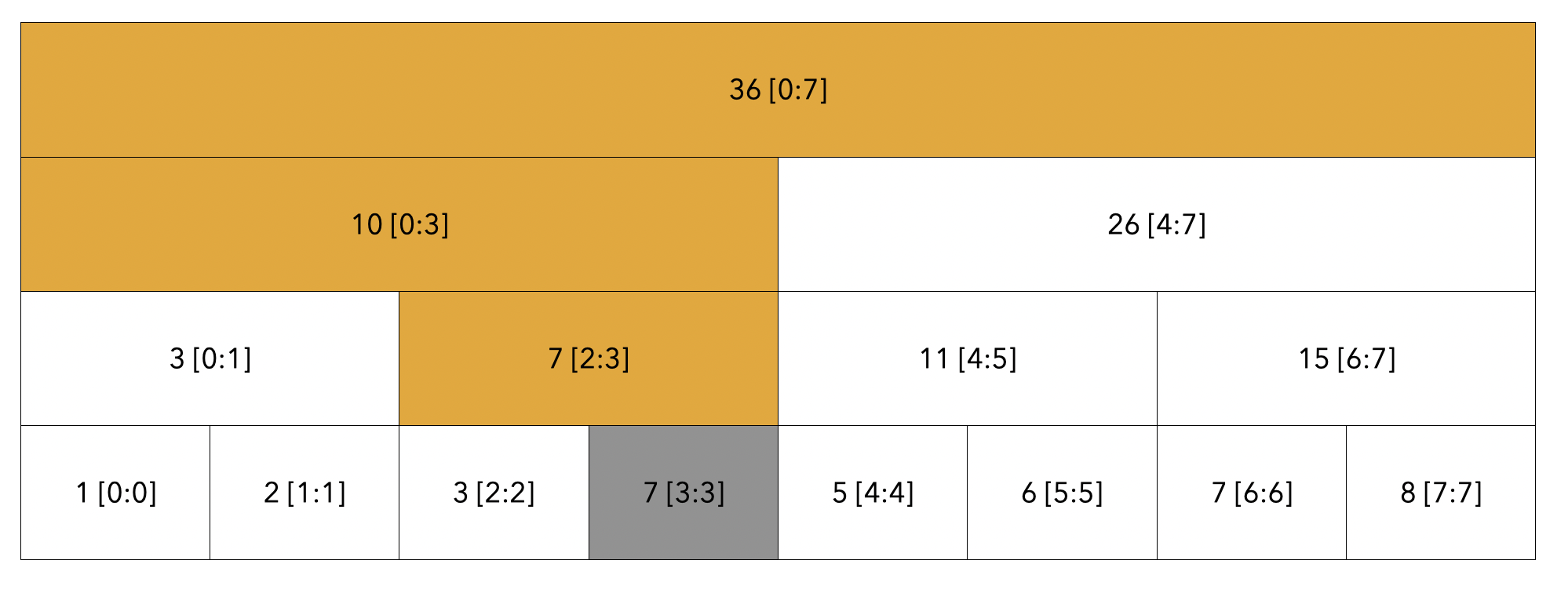
회색 빛의 3번 인덱스는 회색으로 수정됨을 보여드렸습니다. 하지만 3번 인덱스로 인해 노란색으로 칠해진 노드들이 잘못된 값을 가지고 있습니다. 이들의 공통점은 3번 인덱스의 부모노드들로 부모노드들을 업데이트하면 됩니다.

수정의 시간 복잡도

수정은 각 레벨에서 한번씩 이루어지기 때문에 이진트리로 구성된 세그먼트 트리라면 $O(log_2N)$ 의 시간복잡도를 가지게 됩니다.

코드

package segmentTree;

public class SegTree {
    long[] nodes;
    int range;

    SegTree(int[] arr) {
        this.range = arr.length;
        var ncnt = 1;
        while (ncnt<range) ncnt*=2;
        ncnt*=2;
        nodes = new long[ncnt];
        createTree(1, 1, range, arr);
    }

    long createTree(int now, int start, int end, int[] arr) {
        if (start == end) {
            nodes[now] = arr[start - 1];
        } else {
            var mid = (start + end) / 2;
            nodes[now] = createTree(now*2, start, mid, arr) + createTree(now*2+1, mid+1, end, arr);
        }

        return nodes[now];
    }

    long find(int start, int end) {
        return search(1, start, end, 1, range);
    }

    long search(int now, int sStart, int sEnd, int nStart, int nEnd) {
        if (nStart>=sStart && nEnd<=sEnd) return nodes[now];

        var result = 0L;
        var mid = (nStart + nEnd)/2;
        if (mid<sEnd) result += search(now*2+1, sStart, sEnd, mid+1, nEnd);
        if (sStart<=mid) result += search(now*2, sStart, sEnd, nStart, mid);
        return result;
    }

    void modify(int index, int num) {
        findModify(index, num, 1, 1, range);
    }

    long findModify(int index, int num, int now, int start, int end) {
        long result;
        if (start == end) {
            result = num - nodes[now];
            nodes[now] = num;
        } else {
            var mid = (start + end)/2;
            if(mid<index) result = findModify(index, num, now*2+1, mid+1, end);
            else result = findModify(index, num, now*2, start, mid);
            nodes[now] += result;
        }

        return result;
    }
}

정리

	수정	탐색
완전 탐색	$O(1)$	$O(N)$
누적합	$O(N)$	$O(1)$
세그먼트 트리	$O(log_2N)$	$O(log_2N)$

탐색하는 경우가 많고 수정이 적다면 누적합이 가장 유리하다
수정이 많고 탐색하는 경우가 적다면 완전 탐색이 유리하다
수정과 탐색 둘 다 자주 일어난다면 세그먼트 트리가 유리하다

비구름

기본부터 정리해나가는 기록용 블로그

다음 포스트