빅오 표기법 (Big O Notation)

JavaScript 알고리즘 & 자료구조 마스터클래스강의를 듣고 정리한 내용입니다.

1. 문제 해결은 하나가 아니다

하나의 문제에는 여러 해결책이 존재합니다.
우리는 이 가운데 더 좋은 해결책을 선택해야 합니다.
그렇다면, 더 좋은 해결책이란 무엇일까요?

• 실행 속도가 더 빠른?
• 메모리를 덜 사용하는?
• 가독성이 더 좋은?

이런 기준은 상황과 우선 순위에 따라 달라지지만, 성능을 중점으로 둔다면 일반적으로 실행 속도가 가장 중요한 기준이 됩니다.

2. 두 가지 접근 방식의 예시

function A (n) {
  let result = 0;
  for(let i = 1; i <= n; i++){
    result += i;
  }
  return result;
}

function B (n) {
  return n * (n + 1) / 2;
}

숫자 n을 넣으면 1부터 n까지의 합을 반환하는 함수 A, B가 있습니다.
두 함수에 6을 넣으면 1부터 6까지 더해서 21이 출력됩니다.
즉, 두 함수는 같은 인자를 넘겨주면 같은 결과를 반환합니다.

2.1. 실행 시간 비교

두 함수 가운데, 어떤 함수의 실행 속도가 더 빠른지 performance.now()를 활용해서 시간을 직접 측정해보겠습니다.

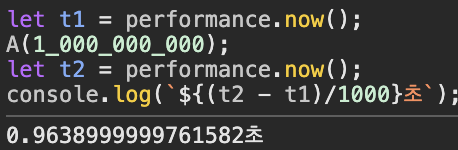
A 함수에 10억을 인자로 넘기면 0.96 초가 소요됩니다.
그러면 같은 수를 B 함수에 넘기면 얼마나 걸릴까요?

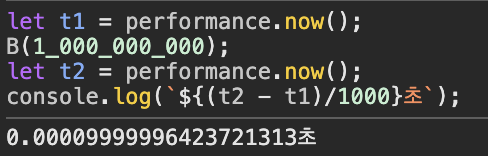
B 함수는 0.0001 초 정도로 A 함수에 비해 적은 시간이 소요되는 걸 확인할 수 있습니다.

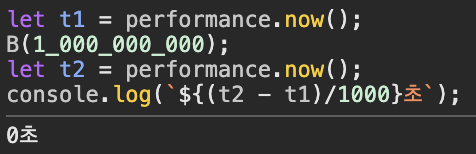
하지만 여러 번 실행하다보면, 조금씩 소요 시간이 바뀌게 되는데요.
그렇다고 해서 A 함수가 B 함수보다 빠르게 나올 정도의 차이는 아니지만, 만약 다른 컴퓨터, 다른 환경이라면 어떨까요?

2.2. 시간 측정의 한계

만약 A를 측정할 때는 백그라운드 작업이 없었고 B는 무거운 작업이 동시에 실행되고 있는 환경이었다면 결과가 바뀔 수도 있습니다.

이처럼 직접 시간을 측정하는 방법은 환경에 영향받기 때문에 신뢰성이 떨어집니다.
어떤 방법으로 측정해야 환경에 영향받지 않고 객관적일 수 있을까요?

2.3. 시간 대신 연산 횟수를 세자

바로 컴퓨터가 실행할 연산 횟수를 세는 방법입니다.
어떤 컴퓨터든 횟수는 같을테니까요.
하지만 로직이 복잡해질 수록 몇 번 할당되고, 몇 번 계산되는지를 일일히 세는 것도 일입니다.

2.4. 연산량의 대략적인 추세만 본다

입력값 n을 0부터 점점 늘린다면, 연산량은 일정한 그래프를 그립니다.

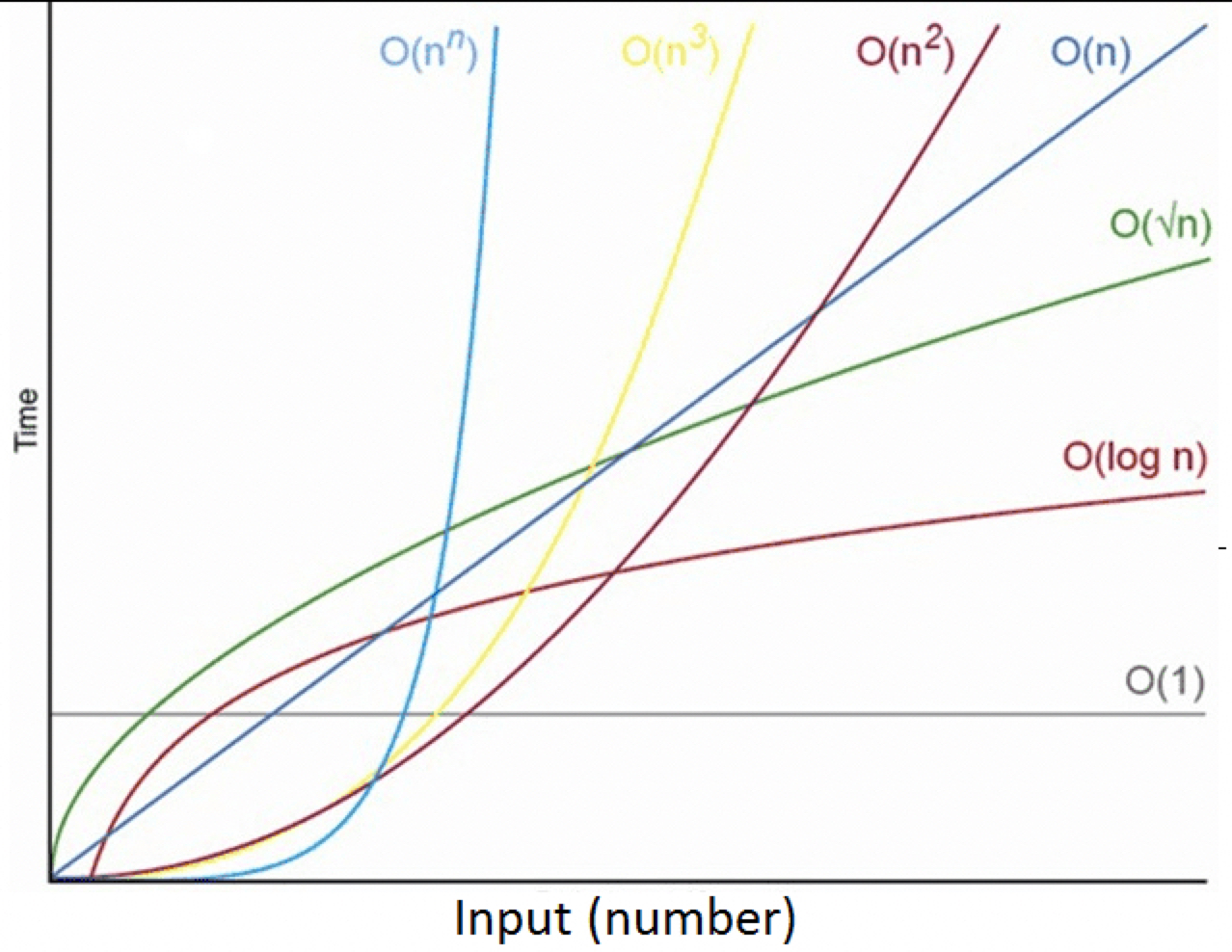
그래프 상에서 본다면 n과 n + 2는 큰 차이를 보이지 않기 때문에 큰 영향을 주는 대략적인 추세만 파악합니다.
n이든 n + 2든 2n이든 똑같이 n으로, 입력값에 상관없이 300번 연산을 한다면 1로 보는 거죠.

3. 빅 오 표기법

입력값에 따른 연산량에 대해 어떤 기준으로 대략적인 추세를 파악할까요?
전체 연산 횟수에서 계수와 상수항은 무시하고, 가장 영향력이 큰 항만을 남긴다.가 기준입니다.

예를 들어 5n² - 3n + 1번 연산하는 알고리즘이 있다면,

• 계수 무시: 5n² - 3n + 1 → n² - n + 1
• 상수항 무시: + 1 → 제거

마지막으로 가장 영향력이 큰 하나의 항만 남겨 O(n²)으로 표기합니다.

O(n²)은 입력값이 커질 수록 연산량이 n의 제곱만큼 증가한다는 의미입니다.
이로써 입력 크기에 따른 알고리즘의 성능을 예측할 수 있습니다.

3.1. 성능을 빠르게 파악하는 기준

실전에서 알고리즘의 성능을 빠르게 예측하기 위해 주의깊게 살펴봐야 할 것들이 있습니다.

대표적으로 반복문입니다.
반복문은 중첩 횟수에 큰 영향을 받습니다.
만약 하나의 반복문이라면 O(n), 두 번 반복문이 중첩되어 있다면 O(n²), 세 번 중첩되어 있다면 O(n³)의 복잡도를 가집니다.

for(...) {...}
for(...) {...}

헷갈리지 말아야 할 것은 반복문이 중첩되지 않고 두 번 실행된다면 O(n + n)이 되므로 O(n)의 복잡도를 갖습니다.

이 밖에도 단순한 사칙 연산이나 조건문만 있다면 상수 시간인 O(1)의 복잡도를 갖고, 이진 탐색이라면 O(log n)의 복잡도를 갖는데요.
앞으로 알고리즘을 공부하면서 탐색, 삽입, 수정, 삭제에서 어떤 복잡도를 갖는지 살펴보겠습니다.