퍼지스트링이란

1. Fuzzy string

근접 문자열 매칭 (Approximate String Matching)

• 유사한 문자열을 찾는 기술
• 근접 문자열 매칭의 응용 사례 : Query spell-checking
• 오류가 포함된 사용자 질의를 자동으로 교정하여 제시해 주는 기능 (예를 들어, 구글의 "이것을 찾으셨나요?")
  

1. 기본 형식 : 불러오기

   require 'fuzzystringmatch'
   jarow=FuzzyStringMatch::JaroWinkler.create( :native)
   p jarow.getDistance("jones",   "johnson")
   'jones'와 'johnson'의 단어 유사도 차이를 알 수 있음.
   jarow.getDistance( "al",        "al"        )
   => 1.0
   
   irb(main):004:0> jarow.getDistance( "dixon",     "dicksonx"  )
   jarow.getDistance( "dixon",     "dicksonx"  )
   => 0.8133333333333332

1. fuzzystring의 원리를 코드 구현

   import numpy as np
   def levenshtein_ratio_and_distance(s, t, ratio_calc = False):
       """ levenshtein_ratio_and_distance:
           Calculates levenshtein distance between two strings.
           If ratio_calc = True, the function computes the
           levenshtein distance ratio of similarity between two strings
           For all i and j, distance[i,j] will contain the Levenshtein
           distance between the first i characters of s and the
           first j characters of t
       """
       # Initialize matrix of zeros
       rows = len(s)+1
       cols = len(t)+1
       distance = np.zeros((rows,cols),dtype = int)
   
       # Populate matrix of zeros with the indeces of each character of both strings
       for i in range(1, rows):
           for k in range(1,cols):
               distance[i][0] = i
               distance[0][k] = k
   
       # Iterate over the matrix to compute the cost of deletions,insertions and/or substitutions    
       for col in range(1, cols):
           for row in range(1, rows):
               if s[row-1] == t[col-1]:
                   cost = 0 # If the characters are the same in the two strings in a given position [i,j] then the cost is 0
               else:
                   # In order to align the results with those of the Python Levenshtein package, if we choose to calculate the ratio
                   # the cost of a substitution is 2. If we calculate just distance, then the cost of a substitution is 1.
                   if ratio_calc == True:
                       cost = 2
                   else:
                       cost = 1
               distance[row][col] = min(distance[row-1][col] + 1,      # Cost of deletions
                                    distance[row][col-1] + 1,          # Cost of insertions
                                    distance[row-1][col-1] + cost)     # Cost of substitutions
       if ratio_calc == True:
           # Computation of the Levenshtein Distance Ratio
           Ratio = ((len(s)+len(t)) - distance[row][col]) / (len(s)+len(t))
           return Ratio
       else:
           # print(distance) # Uncomment if you want to see the matrix showing how the algorithm computes the cost of deletions,
           # insertions and/or substitutions
           # This is the minimum number of edits needed to convert string a to string b
           return "The strings are {} edits away".format(distance[row][col])

2. partial_ratio

   from thefuzz import fuzz,process
   
   s1="Just a test"
   s2="Just a test and some more"
   
   print(fuzz.partial_ratio(s1,s2))
   
   100

3. token_sort_ratio 예시

   • token_sort_ratio는 단어를 토큰화해서 정렬했을때 ratio

   from thefuzz import fuzz,process
   
   s1="Hello World is what I want to tell you"
   s2="What I want to tell you is Hello World"
   
   print(fuzz.ratio(s1,s2))
   print(fuzz.partial_ratio(s1,s2))
   print(fuzz.token_sort_ratio(s1,s2))
   
   61
   61
   100

4. token_set_ratio 예시

   • token_set_ratio는 단어를 list에서 set을 했을 때처럼 uniq하게 요소를 만들어서 비교를 함.

   from thefuzz import fuzz,process
   
   s1="Hello World"
   s2="Hello Hello World World World"
   
   print(fuzz.ratio(s1,s2))
   print(fuzz.partial_ratio(s1,s2))
   print(fuzz.token_sort_ratio(s1,s2))
   print(fuzz.token_set_ratio(s1,s2))
   
   55
   64
   55
   100
   [](https://www.notion.so/8fcecbb95e65428c9353d1caa382a690)

5. process.extract,process.extractOne 예시

   • token_set_ratio는 단어를 list에서 set을 했을 때처럼 uniq하게 요소를 만들어서 비교를 함.

   from thefuzz import fuzz,process
   
   things =["Programming Language","Native Language","React Native","Some Stuff","Hello World","Coding and Stuff"]
   
   print(process.extract("lang",things,limit=2))
   
   print(process.extractOne("lang",things) # 여기에는 limit를 적어주지 않는다. 왜냐하면 One이 limit=1이기 때문
   
   [('Programming Language',90),('Native Language',90)]
   ('Native Language',90)
   

6. process.extract,process.extract 예시2

   from thefuzz import fuzz,process
   
   books =[
   "The Python Bible Volume 1 - Beginner","The Python Bible Volume 2 - Intermediate","The Python Bible Volume 3 - Data Science","The Python Bible Volume 4 - Matching Learning","The Python Bible Volume 5 - Finance","The Python Bible Volume 6 - Neural Net"]
   
   print(process.extract("python data science",books,limit=3))
   
   [("The Python Bible Volume 1 - Beginner",86),(,"The Python Bible Volume 2 - Intermediate",86)]
   ('The Python Bible Volume 3 - Data Sciencee',100)
   

2. **Levenshtein (Edit) distance**

1. **Levenshtein에 대해서**

   Levenshtein distance 는 한 string s1을 s2

   로 변환하는 최소 횟수를 두 string 간의 거리로 정의합니다.

   • PARTY와 PARK가 있다고 가정했을 때

   

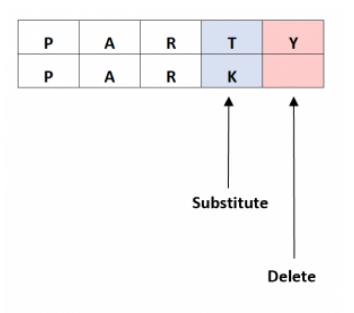
   두 단어 간 Levenshtein에서의 거리는 이와 같이 Subtitute와 Delete가 된다.

   from Levenshtein import distance as lev
   
   lev('party', 'park')

   위의 lev의 결과 값은 2가 된다.
   

2. 리스트 안에서 요소간의 distance값을 바로 돌린 경우

   #define arrays
   a = ['Mavs', 'Spurs', 'Lakers', 'Cavs']
   b <- ['Rockets', 'Pacers', 'Warriors', 'Celtics']
   
   #calculate Levenshtein distance between two arrays
   for i,k in zip(a, b):
     print(lev(i, k))

   • The Levenshtein distance between ‘Mavs’ and ‘Rockets’ is 6.
   • The Levenshtein distance between ‘Spurs’ and ‘Pacers’ is 4.
   • The Levenshtein distance between ‘Lakers’ and ‘Warriors’ is 5.
   • The Levenshtein distance between ‘Cavs’ and ‘Celtics’ is 5.