
해시 테이블과 해시 테이블을 사용하면서 발생하는 상황에 대해서 정리해보겠습니다.
❓ 해시 테이블이란?
"해시 테이블은 연관 배열 구조를 이용하여 key에 value를 저장하는 자료구조입니다" -> 위키백과 정의
다른 말로 표현 하면 데이터를 효율적으로 관리하기 위해, 임의의 길이 데이터를 고정된 길이의 데이터로 매핑하는 것이라고 할 수 있습니다.!
✅ 연관 배열이란?
연관 배열(associative array)은 자료 구조의 하나로, 키 하나와 값 하나가 연관되어 있으며 키를 통해 연관 되는 값을 얻을 수 있습니다.
해시 함수를 구현하여 데이터 값을 해시 값으로 매핑합니다.
yoon → 해싱함수 → 5
Kim → 해싱함수 → 3
Park → 해싱함수 → 2
Chun → 해싱함수 → 5 // yoon와 해싱값 충돌위와 같이 결국에는 데이터가 많아지면, 다른 데이터가 동일한 해시 값을 가르키는 *충돌(Collision) 현상이 발생합니다.
✅ 그런데도 왜 해시 테이블을 왜 사용할까??
해시 테이블은 적은 자원으로 많은 데이터를 효율적으로 관리하기 위해 사용합니다. 하드 디스크나, 클라우드에 존재하는 무한한 데이터들을 유한한 개수의 해시 값으로 매핑하면 작은 메모리로도 프로세스의 관리가 가능해 집니다.
위에서 해시 테이블은 적은 자원으로 많은 데이터를 효율적으로 관리하기 위해 사용한다. 했습니다.
그렇다면 "어떻게 적은 자원으로 많은 데이터를 효율적으로 관리할까??" 라는 궁금증이 생깁니다. 이는 해시 테이블의 충돌 해결을 보면서 궁금증을 해소 하겠습니다.
✅ 해시 테이블은 왜 빠를까??
색인(index) 에 해시 값을 사용함으로써 모든 데이터를 살피지 않아도 탐색과 삽입/삭제 을 빠르게 수행 가능합니다.
해시 함수는 언제나 동일한 해시 값을 리턴하고, 해당 index만 안다면 해시 테이블 크기와 상관없이 데이터에서 대단히 빠르게 접근 할 수 있습니다.
위와 같은 특성 덕분에 해시 테이블 탐색/삽입,삭제의 시간 복잡도 O(1) 라는 특성이 있습니다.
📌 해시 테이블의 충돌 발생
✅ 해시 충돌이란?
위에서도 예시를 들어 설명 했지만 한번 더 얘기하면, 해시 충돌은 해시 함수가 서로 다른 두 개의 입력 값에 대해 동일한 출력 값을 내는 상황을 말합니다. 주로 예시로 비둘기 집의 원리가 나옵니다.

비둘기는 비둘기 집에 들어가야 합니다. 하지만 이미 비둘기 집에 비둘기가 있는 경우 충돌 현상이 일어나게 됩니다.
이러한 상황을 해결 하기 위해 해시 테이블에서는 여러 해결 방안이 나옵니다.
✅ 해시 테이블 충돌 문제 해결
-
체이닝 방법: 연결 리스트로 노드를 계속해서 추가해 나가는 방식 (제한 없이 계속 연결이 가능, but 메모리 문제 발생)
-
Open Addressing 방법 : 해시 함수로 얻은 주소가 아닌 다른 주소에 데이터를 저장할 수 있도록 허용 (해당 키 값에 저장 되어있으면 다음 주소에 저장)
* 제곱 탐사 : 정해진 고정 폭을 제곱수로 옮겨 해시 값의 중복을 피함 * 선형 탐사: 정해진 고정 폭으로 옮겨 해시 값의 중복을 피함 * 이중 해싱: 충돌이 발생한 경우 기존과 다른 해싱 함수를 사용하여 인덱싱 하여 해시 값의 중복을 피함체이닝 방법은 충돌 시 연결 리스트를 만들어 값을 할당하고 이어서 연결하는 방식을 사용합니다.
Open Addressing 방법은 충돌 시 해시 테이블에서 놀고 있는 인덱스에 할당하는 방식을 사용합니다.
✅ Seperate Chaning(분산 체이닝) 방법
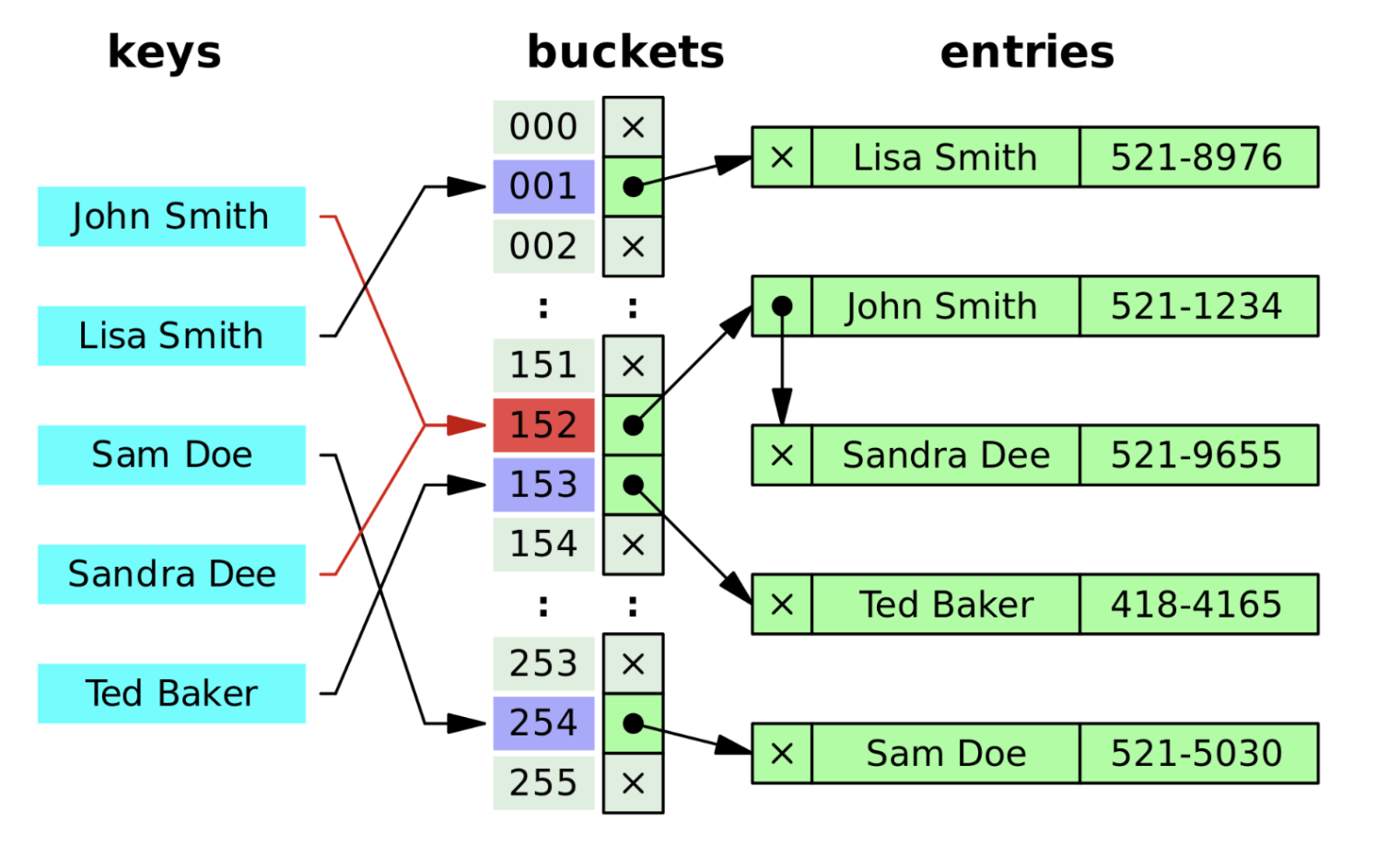
위 그림은 분산 체이닝 방법을 사용하여 해시 충돌을 해결한 그림입니다.
동일한 인덱스를 받아 충돌이 생겼을 때, index가 가르키고 있는 연결 리스트에 노드를 추가하여 값을 추가 해줍니다. 이렇게 하면 데이터를 추가 할때 동일한 인덱스를 받아 충돌이 발생한 경우, 데이터 삽입에 문제가 없습니다. 데이터 추출 시에는 key에 대한 index로 연결 리스트를 탐색(순회)하며 데이터를 추출 합니다.
하지만 여기에는 단점이 있습니다. 동일한 인덱스를 받아 충돌을 체이닝으로 계속 해결하게 된다면 버킷의 할당 된 테이블이 놀고 있는 현상이 일어납니다.
이러한 문제, 즉 놀고 있는 버킷의 테이블을 먼저 소모하도록 만든 충돌 해결 방법이 바로 Open Addressing 방법 입니다.
위에서 소개한 Open Addressing 방법 중 선형 탐사 방법에 대해 알아 보겠습니다.
✅ Linear Probing(선형 탐사)
선형 탐사 방법은 버킷의 자리를 우선적으로 모두 사용하는 방식 입니다. 테이블의 한 칸씩 이동하며 값이 없다면 할당하고, 있다면 다시 한 칸 이동합니다.
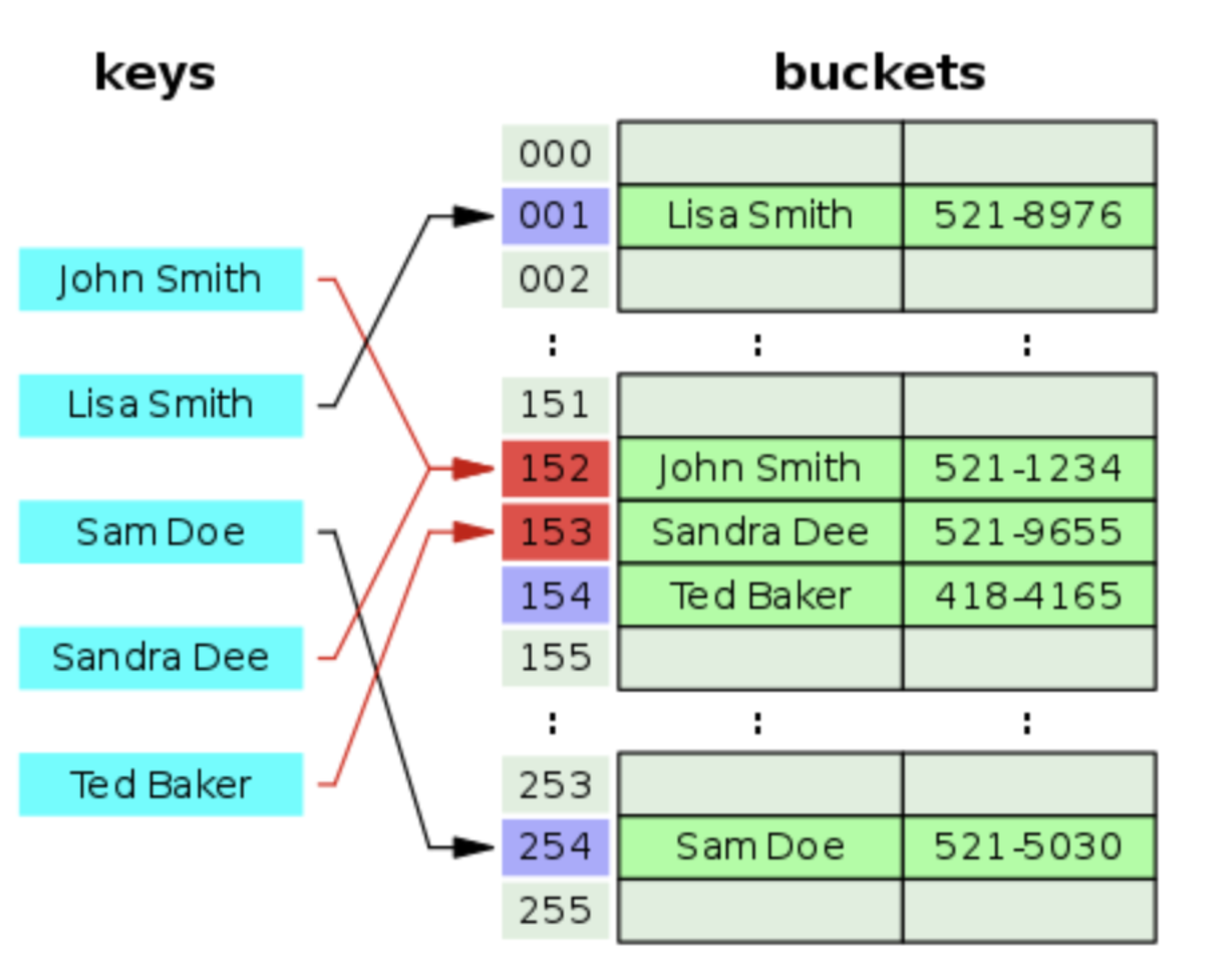
위 그림을 보면 충돌이 생겼을 때 다음 인덱스로 할당해 주는 것을 볼 수 있습니다. 하지만 계속해서 선형 탐사 방식으로 충돌을 해결하다보면 테이블이 모두 차게 되는 경우가 생깁니다.
이러한 경우 더 이상 요소를 넣어 줄 수 없기 때문에 테이블의 크기를 늘려 주어야 합니다.
이때 테이블 Resizing 을 통해 테이블의 크기를 늘려줍니다. 보통 75% 만큼 채워진다면, 2배로 테이블의 크기를 늘려주고 25% 로 줄었다면 테이블의 크기를 절반으로 줄여줍니다.
😆 정리
해시 테이블의 충돌을 해결하기 위한 전략은 크게 두 가지로 체이닝 방법과 Open Addressing 방법이 있습니다. 체이닝 방법은 연결리스트를 만들어 값을 할당하는 방식이며, 새로 리스트를 만든다는 점에서 공간 메모리 측면에서 비효율적입니다. Open Addressing 방식은 비어있는 인덱스에 값을 할당하는 방식으로 모든 인덱스에 값이 할당 되어 있는 경우 resizing 방식으로 해시 테이블의 크기를 늘려 해결합니다. 하지만 한정된 공간의 해시 테이블을 사용하는 경우 적합하지 않을 수 있습니다. 상황에 따라 체이닝을 통한 충돌 해결, 오픈 어드레싱 방법을 통한 충돌 해결을 골라 사용하면, 효율적인 자료 관리가 될 수 있습니다.
