[DataStructure&Algorithm] Heap

윤장원·2021년 2월 16일
datastructure알고리즘
0

DataStructure & Algorithm

목록 보기
3/5

힙(heap)

  • 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조입니다.
  • 여러 개의 값들 중에서 최대값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조입니다.
  • 힙은 일종의 반정렬상태(느슨한정렬) 를 유지합니다.
    • 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도
    • 간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말합니다.
  • 힙 트리에서는 중복된 값을 허용합니다. (이진 탐색 트리에서는 중복된 값을 허용하지 않습니다.)

힙의 조건 : 완전 이진 트리이며 , 아래에서 설명할 최대 힙 , 최소 힙의 조건을 충족 해야한다.

힙의 종류

  • 최대 힙 (max Heap)
    • 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진트리
    • key(부모 노드) => key(자식 노드)
  • 최소 힙(min heap)
    • 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
    • key(부모 노드) <= key(자식 노드)

힙(heap)의 구현

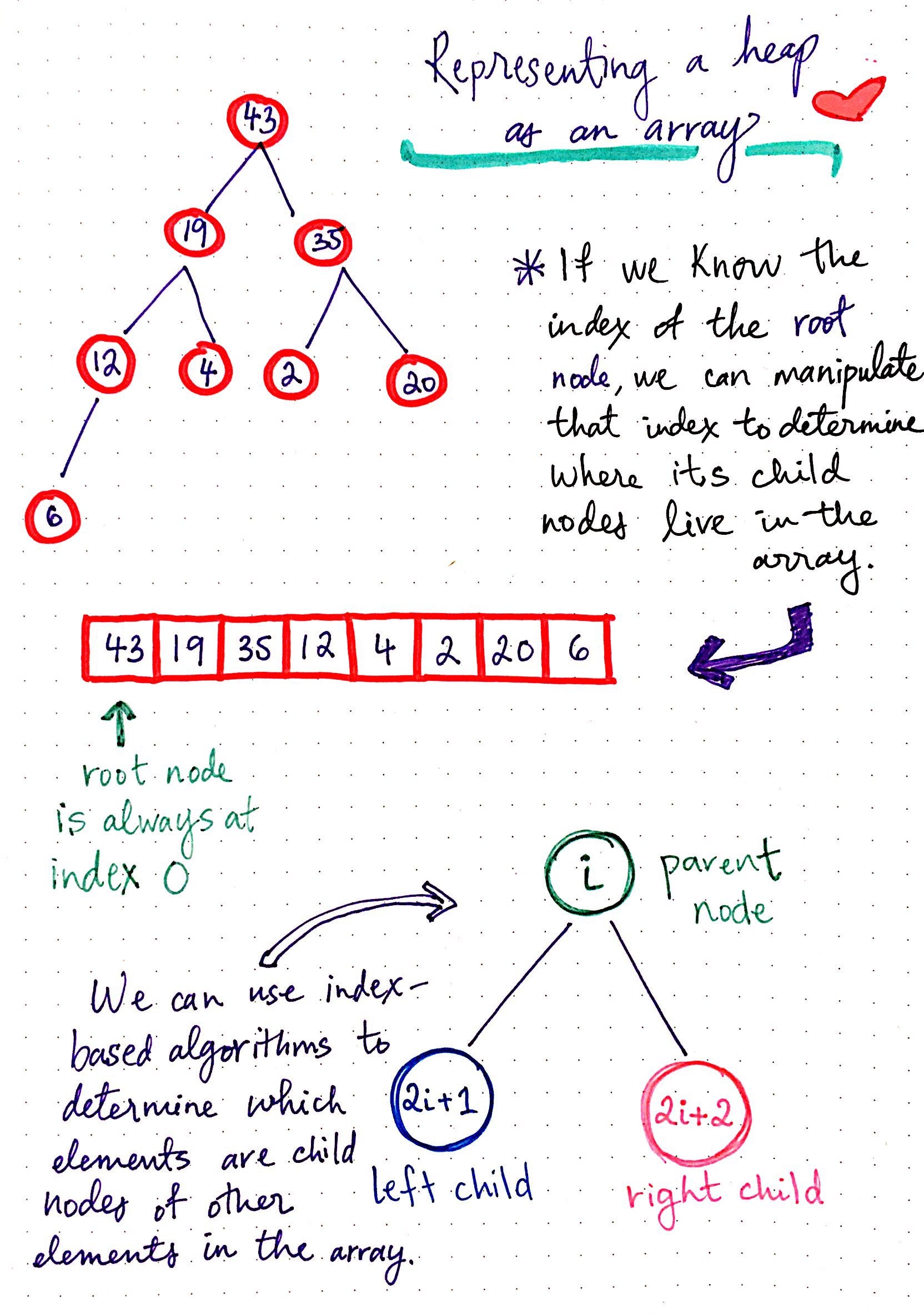
  • 힙을 저장하는 표준적인 자료구조는 배열 입니다.
  • 구현을 쉽게 하기 위하여 첫 번째 인덱스인 0은 사용되지 않습니다.
  • 특정 위치의 노드 번호는 새로운 노드가 추가 되어도 변하지 않습니다.
    • ex) 루트 노드의 오른쪽 노드 번호는 항상 3입니다.
  • 힙에서의 부모 노드와 자식 노드의 관계
    • 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
    • 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
    • 부모의 인덱스 = (자식의 인덱스) / 2

힙의 삭제

  • 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.
    • 최대 힙(max Heap)에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.
  • 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
  • 힙을 재구성한다.

최대 힙 코드

class MaxHeapTree {
  // 편리한 구현을 위해 index는 1부터 사용
  constructor() {
    this._items = [""];
  }

  get items() {
    return this._items;
  }

  get root() {
    return _items[1];
  }

  /**
   * 구현 절차
   * - 1) 힙의 가장 마지막 위치(배열의 마지막)에 노드에 추가한다
   * - 2) 힙의 조건을 만족시키도록 연산 (부모노드와 교환)
   *  - 새로 추가한 노드와 부모 노드를 비교하여 부모노드가 더 작으면 위치를 바꾼다
   *  - (더 큰 부모노드가 없을때까지 반복)
   */
  insert(key) {
    this._items.push(key);
    this._allignAfterInsert();
  }

  /**
   * 힙의 삭제는 루트 노드 삭제만 구현한다. (queue의 pop 연산이라고 생각하면 됨)
   *
   * 구현 절차
   * - 1) 루트노드를 제거
   * - 2) 제거한 루트노드자리에 마지막 노드를 삽입
   * - 3) 힙의 조건을 만족시키도록 연산
   *  - 루트노드의 자식노드 중 더 큰 값과 교환한다.
   *  - (더 큰 자식노드가 없을때까지 반복)
   */

  remove() {
    this._items[1] = this._items.pop();
    this._allignAfterRemove();
  }

  _allignAfterInsert() {
    let childIndex = this._items.length - 1;
    let child = this._items[childIndex];

    let parentIndex = Math.floor(childIndex / 2) || 1;
    let parent = this._items[parentIndex];

    let newChildIndex;
    while (parent < child) {
      newChildIndex = parentIndex;
      this._items[newChildIndex] = child;
      this._items[childIndex] = parent;

      parentIndex = Math.floor(newChildIndex / 2) || 1;
      parent = this._items[parentIndex];
      childIndex = newChildIndex;
    }
  }

  _allignAfterRemove() {
    let parentIndex = 1;
    let parent = this._items[parentIndex];

    let leftChild = this._items[parentIndex * 2];
    let rightChild = this._items[parentIndex * 2 + 1];

    let bigChild = leftChild > rightChild ? leftChild : rightChild;
    let bigChildIndex = this._items.indexOf(bigChild);

    let newParentIndex;
    while (parent < bigChild) {
      newParentIndex = bigChildIndex;
      this._items[newParentIndex] = parent;
      this._items[parentIndex] = bigChild;

      leftChild = this._items[newParentIndex * 2];
      rightChild = this._items[newParentIndex * 2 + 1];

      bigChild = leftChild > rightChild ? leftChild : rightChild;
      bigChildIndex = this._items.indexOf(bigChild);
      parentIndex = newParentIndex;
    }
  }
}

// Test
it("MaxHeapTree 클래스는 잘 동작한다.", () => {
  const heap = new MaxHeapTree();

  heap.insert(9);
  heap.insert(3);
  heap.insert(5);
  heap.insert(10);
  heap.insert(6);
  expect(heap.items).toEqual(["", 10, 9, 5, 3, 6]);

  heap.insert(8);
  expect(heap.items).toEqual(["", 10, 9, 8, 3, 6, 5]);

  heap.remove();
  expect(heap.items).toEqual(["", 9, 6, 8, 3, 5]);
  heap.remove();
  expect(heap.items).toEqual(["", 8, 6, 5, 3]);
});

최소 힙

class MinHeapTree {
  // 편리한 구현을 위해 index는 1부터 사용
  constructor() {
    this._items = [""];
  }

  get items() {
    return this._items;
  }

  get root() {
    return _items[1];
  }

  /**
   * 구현 절차
   * - 1) 힙의 가장 마지막 위치(배열의 마지막)에 노드에 추가한다
   * - 2) 힙의 조건을 만족시키도록 연산 (부모노드와 교환)
   *  - 새로 추가한 노드와 부모 노드를 비교하여 부모노드가 더 크면 위치를 바꾼다
   *  - (더 큰 부모노드가 없을때까지 반복)
   */
  insert(key) {
    this._items.push(key);
    this._allignAfterInsert();
  }

  /**
   * 힙의 삭제는 루트 노드 삭제만 구현한다. (queue의 pop 연산이라고 생각하면 됨)
   *
   * 구현 절차
   * - 1) 루트노드를 제거
   * - 2) 제거한 루트노드자리에 마지막 노드를 삽입
   * - 3) 힙의 조건을 만족시키도록 연산
   *  - 루트노드의 자식노드 중 더 작은 값과 교환한다.
   *  - (더 작은 자식노드가 없을때까지 반복)
   */
  remove() {
    this._items[1] = this._items.pop();
    this._allignAfterRemove();
  }

  _allignAfterInsert() {
    let childIndex = this._items.length - 1;
    let child = this._items[childIndex];

    let parentIndex = Math.floor(childIndex / 2) || 1;
    let parent = this._items[parentIndex];

    let newChildIndex;
    while (parent > child) {
      newChildIndex = parentIndex;
      this._items[newChildIndex] = child;
      this._items[childIndex] = parent;

      parentIndex = Math.floor(newChildIndex / 2) || 1;
      parent = this._items[parentIndex];
      childIndex = newChildIndex;
    }
  }

  _allignAfterRemove() {
    let parentIndex = 1;
    let parent = this._items[parentIndex];

    let leftChild = this._items[parentIndex * 2];
    let rightChild = this._items[parentIndex * 2 + 1];

    let smallChild = leftChild < rightChild ? leftChild : rightChild;
    let smallChildIndex = this._items.indexOf(smallChild);

    let newParentIndex;
    while (parent > smallChild) {
      newParentIndex = smallChildIndex;
      this._items[newParentIndex] = parent;
      this._items[parentIndex] = smallChild;

      leftChild = this._items[newParentIndex * 2];
      rightChild = this._items[newParentIndex * 2 + 1];

      smallChild = leftChild < rightChild ? leftChild : rightChild;
      smallChildIndex = this._items.indexOf(smallChild);
      parentIndex = newParentIndex;
    }
  }
}

// Test
it("MinHeapTree 클래스는 잘 동작한다.", () => {
  const heap = new MinHeapTree();

  heap.insert(9);
  heap.insert(3);
  heap.insert(5);
  heap.insert(10);
  heap.insert(6);
  expect(heap.items).toEqual(["", 3, 6, 5, 10, 9]);

  heap.insert(2);
  expect(heap.items).toEqual(["", 2, 6, 3, 10, 9, 5]);

  heap.remove();
  expect(heap.items).toEqual(["", 3, 6, 5, 10, 9]);
  heap.remove();
  expect(heap.items).toEqual(["", 5, 6, 9, 10]);
});

레퍼런스 코드

class Heap {
  constructor(size) {
    if (size && isNaN(size)) throw Error(`Invalidate param`);

    this.idx = 0;
    this.arr = new Array(size ? size : 11).fill(null);
  }

  add(n) {
    if (this.idx + 1 === this.arr.length) throw Error(`Stack overflow`);

    let idx = ++this.idx;
    this.arr[idx] = n;

    while (idx > 1) {
      const nextIdx = idx >> 1;
      const parent = this.arr[nextIdx];
      const cur = this.arr[idx];

      if (parent <= cur) break;

      this.arr[nextIdx] = cur;
      this.arr[idx] = parent;

      idx >>= 1;
    }

    return true;
  }

  print() {
    console.log(this.arr);
  }

  pop() {
    if (this.idx === 0) throw Error(`Empty stack`);

    const ret = this.arr[1];
    let idx = 1;

    this.arr[1] = this.arr[this.idx];
    this.arr[this.idx--] = null;

    while (idx < this.idx) {
      if (idx * 2 > this.idx || idx * 2 + 1 > this.idx) break;

      let nextIdx = idx * 2;
      if (this.arr[idx] <= this.arr[nextIdx]) nextIdx = idx;
      if (this.arr[nextIdx] > this.arr[idx * 2 + 1]) nextIdx = idx * 2 + 1;
      if (nextIdx === idx) break;

      const tmp = this.arr[idx];
      this.arr[idx] = this.arr[nextIdx];
      this.arr[nextIdx] = tmp;
      idx = nextIdx;
    }

    return ret;
  }

  peek() {
    return this.arr[this.idx];
  }
}

function main() {
  const heap = new Heap();
  for (let i = 10; i > 0; i--) {
    heap.add(i);
  }
  heap.print();
  while (heap.peek()) {
    console.log(heap.pop(), heap.idx);
    heap.print();
  }
}

main();
  • 레퍼런스 코드

const Heap = function Heap() {
  this.heap = Array(30).fill(' ');
  this.heapSize =0;
}

Heap.prototype.insertHeap = function(data) {
  const heap = this.heap;
  const newData = data;
  if(this.heapSize === 0) {
    heap[1] = newData;
    this.heapSize++;
  }else {
    this.heapSize++
    let idx = this.heapSzie;

    heap[idx] = newData;

    // 데이터를 넣었으면 비교 연산

    let parentIdx = parseInt(idx/2);

    while(parentIdx > 0) {
      if(heap[parentIdx]< heap[idx]) {
        let temp = heap[parentIdx];
        heap[parentIdx] = heap[idx];
        heap[idx] = temp;
      }else{
        break;
        parentIdx = parseInt(parseInt / 2);
      }
    }
  }
}

Heap.prototype.printAll = function () {
  let result = "";
  
  for(let i=0; i< this.heapSize; i++) {
    result += `${this.heap[i]}`;
    console.log("출력", result);
  }
}

Heap.prototype.deleteHeap = function() {
  const lastIdx = this.heapSize;
  const heap = this.heap;
  const deleteVal = heap[i];
  let idx = 1;
  
  console.log(heap);

  heap[1] = heap[lastIdx];
  heap[lastIdx] = "";

  while(heap[idx * 2] !== "" && heap[idx*2+1] !=="") {
    let temp = 0; 
    if(heap[idx] < heap[idx*2]){
      temp = heap[idx];
      heap[idx] = heap[idx*2];
      heap[idx*2] = temp;
      idx *= 2;
    }
    else if(heap[idx] < heap[idx*2+1]) {
      temp = heap[idx];
      heap[idx] = heap[idx*2+1];
      heap[idx*2+1] = temp;
      idx = idx*2+1;
    }else{
      break;
    }
  }

  console.log(`${delteVal} 삭제완료` );
}


function main() {
  const heap = new Heap();
  heap.insertHeap(23);
  heap.insertHeap(19);
  heap.insertHeap(10);
  heap.insertHeap(15);
  heap.insertHeap(9);
  heap.insertHeap(13);

  heap.deleteHeap();
  heap.printAll();
}

main();

reference

profile
윤장원
어제보다 오늘 더 노력하는 프론트엔드 개발자
이전 포스트

[DataStructure&Algorithm] BFS(너비우선 탐색)

다음 포스트

우선 순위 큐는 어떻게 작동하는 가?

0개의 댓글