기수 정렬(Radix sort)

기수 정렬 원리

• 비교 정렬들의 평균적인 시간 복잡도 한계는 n log n이다. 더 빠른 정렬 알고리즘은 없을까?
• 더 빠른 정렬 알고리즘이라고 간주되는 알고리증 중 기수 정렬이 있다.
• 그러나 기수 정렬은 숫자에 대해서만 정렬할 수 있다. 또한, 그 대상들을 직접 비교하지는 않는다는 것이 특징이다
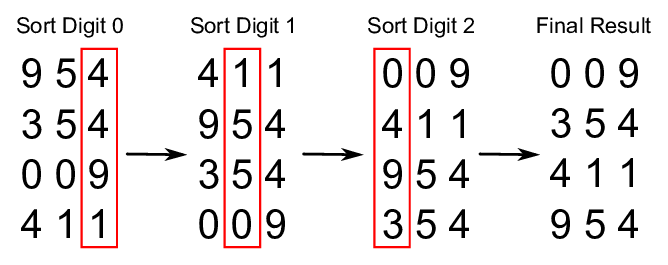
• 기수 정렬은 숫자의 크기에 대한 정보가 숫자의 자릿수 에 이미 저장되어 있다는 사실을 이용한다.
• 기수 정렬에서는 각 자릿수의 숫자를 나눠 담아야 하고, 이를 가장 큰 자리수까지 반복한다. 십진법 수들을 정렬한다면, 10개의 버킷에 0부터 9까지 1의 자릿수의 수들을 비교해서 나눠 담고, 버킷에 들어가 있는 순서로 정렬됐다. 만약 정렬하는 수 중에서 10의 자리의 수도 있다면, 앞서 정렬된 수들을 다시 10개의 버킷에 0부터 9까지 10의 자릿수의 수들을 비교해서 나눠 담고, 버킷에 들어가 있는 순서대로 정렬됐다. 이처럼 정렬하는 수 중에서 가능한 최고 자리의 수까지 이 과정을 반복한다.
  

기수 정렬 헬퍼 함수

• getDigit(num, i) : 숫자 num의 i번째(1의 자리는 0부터) 자릿수의 수를 반환

function getDigit(num,i) {
	return Math.floor(Math.abs(num) / Math.pow(10, i) % 10;
}

console.log(getDigit(1234,3)) // 1

• digitCount(num) : num이 최대 자릿수를 반환

function digitCount(num) {
  if (num === 0) return 1;
  return Math.floor(Math.log10(Math.abs(num))) + 1;
}

console.log(digitCount(423)); // 3

• mostDigits(nums) : 숫자들의 배열을 입력하면 그 중 자릿수가 가장 큰 수의 자릿수를 알려준다.
  • 위에서 만든 digitCount(num) 함수를 사용한다.

function mostDigits(nums) {
  let maxDigits = 0;
  for (let i = 0; i < nums.length; i++) {
    maxDigits = Math.max(maxDigits, digitCount(nums[i]));
  }
  return maxDigits;
}

console.log(mostDigits([23, 123, 568, 844423, 1 ]))
// 6

기수 정렬 코드

• 기수정렬(radixSort) 자바스크립트 코드
  • 위에서 정의한 헬퍼함수들을 활용한다.

function getDigit(num,i) {
	return Math.floor(Math.abs(num) / Math.pow(10, i) % 10;
}

function digitCount(num) {
  if (num === 0) return 1;
  return Math.floor(Math.log10(Math.abs(num))) + 1;
}

function mostDigits(nums) {
  let maxDigits = 0;
  for (let i = 0; i < nums.length; i++) {
    maxDigits = Math.max(maxDigits, digitCount(nums[i]));
  }
  return maxDigits;
}

function radixSort(nums) {
  let maxDigitCount = mostDigits(nums); 
  for (let k = 0; k < maxDigitCount; k++) {
    let digitBuckets = Array.from({ length: 10 }, () => []);
    for (let i = 0; i < nums.length; i++) {
      let digit = getDigit(nums[i], k);
      digitBuckets[digit].push(nums[i]); 
    }
    nums = [].concat(...digitBuckets); 
  }
  return nums;
}

console.log(radixSort([23, 345, 5467, 12, 2345, 9852]));
// [ 12, 23, 345, 2345, 5467, 9852 ]

• 코드 설명
  • 입력된 배열의 숫자들 중에서 가장 큰 자릿수를 maxDigitCount에 할당한다.(헬퍼함수 mostDigits(nums))
  • 가장 큰 자릿수인 maxDigitCount만큼 루프(인덱스: k)를 돈다.
    • 빈 배열 10개가 담긴 배열을 digitBuckets에 할당한다.
    • 입력된 배열의 요소들의 개수만큼 루프(인덱스: i)를 돈다.
      • 배열의 i번째 요소인 숫자(nums[i])를 그 숫자의 k번째(1의 자리는 0부터) 자릿수(헬퍼함수 getDigit(nums[i], k))에 해당하는 버킷의 자리(digitBukcets[인덱스])에 넣는다.
    • 각 자릿수의 루프를 마칠 때마다 해당 루프에서 저장된 digitBuckes 배열의 요소를 평탄화하여 하나로 합친 배열을 재할당한다.
  • 모든 자릿수의 루프가 종료되면, 마지막에 재할당된 배열을 반환한다.

참고 문법

• 빈 배열 여러 개를 만드는 방법
  • Array.from() 메서드를 활용하여 한 배열 안에 빈 배열을 여러 개 만들 수 있다.

console.log(Array.from({ length: 10 }, () => []));
// [ [], [], [], [], [], [], [], [], [], [] ]

console.log(Array.from({ length: 10 }, () => ["Hi"]));
// [ [ 'Hi' ], [ 'Hi' ], [ 'Hi' ], [ 'Hi' ] ]

• 배열 안에 요소로 있는 배열들을 하나의 배열로 합치기
  • concat 메서드와 spread 연산자(...) 사용

console.log([].concat(...[[1], [2], [3]])); // [1, 2, 3]

기수 정렬 성능

아래에서 n은 정렬하는 숫자의 개수(배열의 길이)이고, k는 숫자들 중 가장 큰 수의 자릿수(길이)이다.

정말 긴 숫자가 있다면 실행 시간에 영향을 미친다.

• 시간복잡도
  • Best : $O(nk)$
  • Average: $O(nk)$
  • Worst: $O(nk)$
• 공간복잡도
  • $O(n+k)$

기수 정렬이 이론상으로는 다른 비교정렬의 시간복잡도인 $nlogn$보다 빠르다고 볼 수도 있으나, 이에 대해서는 논쟁의 여지가 있다. 만약에 자릿수 k에 $log n$ 이 들어간다면 시간복잡도는 $n log n$이 될 것이고, 결국 비교 정렬의 시간복잡도와 같게 된다. 이러한 주장을 받아들이면 기수 정렬은 다른 비교 정렬과 같은 시간복잡도를 가지므로, 생각보다 빠르지 않다는 것이다.

컴퓨터가 정보를 실제로 어떻게 저장하는지에 따라서 다를 수 있다.