트리(Tree) 자료구조

트리

• 트리는 parent , child 관계를 지닌 노드들로 구성된 자료구조다.

• 노드들로 구성됐다는 점에서 연결리스트와 비슷하다.

  • 하지만 리스트는 일렬로 쭉 이어지는 선형(linear) 구조인 반면에,
  • 트리는 여러 갈래로 뻗을 수 있는 비선형(nonlinear) 구조이다.
    • 어떻게 보면, 단일 연결 리스트는 트리의 한 종류로 볼 수 있다.

• 트리에서 노드는 부모-자식 관계에 따라 자식인 노드만을 가리킬 수 있다. 부모나 형제를 가리키는 노드가 있어서는 안 된다.

• 또한 출발점(루트)는 하나여야 한다.

• 트리 용어 정리

  • Root : 트리의 최상위 노드이다.
  • Child : 루트에서 멀어질 때 다른 노드에 직접 연결된 노드이다.
  • Parent : Child의 반대 개념이다
  • Siblings : 부모가 동일한 노드 그룹이다.
  • Leaf : 하위에 Child가 없는 노드이다.
  • Edge(간선) : 한 노드와 다른 노드 간의 연결이다. 화살표

• 트리 활용 사례

  • HTML DOM
    • document.body 도 객체이고, 이에 대해 사용할 수 있는 메서드가 있다. body의 child(하위 태그)는 document.body.children 를 통해 체이닝하여 확인할 수 있다.
  • Network Routing
  • Abstract Syntax Tree

이진 탐색 트리(BST, Binary Search Tree)

• 이진 트리(Binary Tree)는 트리의 일종이다.
  • 이진 트리는 각 노드가 최대 두 개의 자식을 가져야한다는 규칙이 있다. 따라서 각 노드의 자식이 0개거나 1개거나 2개일 수 있다. 이러한 이진 트리의 구조는 순회가 쉽다는 강점이 있다.
• 그리고 이진 탐색 트리는 이진 트리의 특별한 종류이다. 용어 그대로 이진 트리 중에서 탐색에 더욱 강점이 있는 자료구조다.
• 이진 탐색 트리 정의
  • 모든 부모 노드는 최소한 두 자식 노드를 갖는다.
  • 부모 노드의 왼쪽에 있는 모든 노드는 항상 부모보다 작다.
  • 부모 노드보다 오른쪽에 있는 모든 노드는 언제나 부모보다 크다.

이진탐색트리 기본구조

class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
}

이진탐색트리의 Insert 메서드

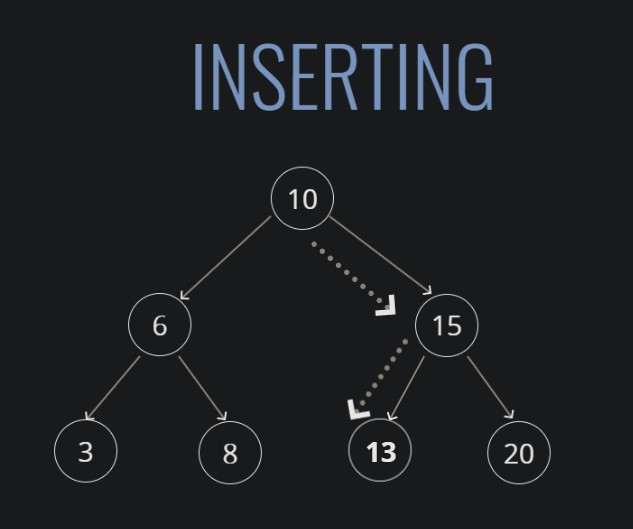
 insert(value) {
    const newNode = new Node(value);
   // root가 없으면 새 노드가 root가 되고 끝난다.
    if (this.root === null) {
      this.root = newNode;
      return this;
    }
   // root가 있으면, root부터 아래로 순회하면서 값이 들어가야 할 곳을 찾는다.
    let current = this.root;
    while (true) {
      if (value === current.value) return undefined;
      // 삽입할 값이 현재 순회하고 있는 노드의 값보다 작고, 
      if (value < current.value) {
        // 현재 순회하는 노드의 왼쪽 child가 비었다면, 그 자리에 값을 넣고 return한다. 
        if (current.left === null) {
          current.left = newNode;
          return this;
        }
        // 그렇지 않다면, 현재 순회하는 노드의 왼쪽 child를 순회하기 시작한다.
        current = current.left;
        // 삽입할 값이 현재 순회하고 있는 노드의 값보다 크고, 
      } else {
        // 현재 순회하는 노드의 오른쪽 child가 비었다면, 그 자리에 값을 넣고 return한다. 
        if (current.right === null) {
          current.right = newNode;
          return this;
        }
        // 그렇지 않다면, 현재 순회하는 노드의 오른쪽 child를 순회하기 시작한다.
        current = current.right;
      }
    }
  }

이진탐색트리의 Find 메서드

• Find 또한 Insert와 로직이 비슷하다.

  find(value) {
    // root가 비었으면 false 반환하고 종료
    if (this.root === null) return false;
    // 현재 순회하는 노드가 있고 아직 값을 찾지 못했다면 while문을 계속 돈다.
    let current = this.root; 
    while (current) {
      // 현재 순회하는 노드의 값이 찾는 값과 같으면, 노드를 반환하고 반복문 종료한다.
      if (value === current.value) return current; 
      
      // 현재 순회하는 노드의 값이 찾는 값보다 크면 다음으로 순회할 노드는 왼쪽 child다.
      if (value < current.value) {
        current = current.left; 
        // 현재 순회하는 노드의 값이 찾는 값보다 작으면 다음으로 순회할 노드는 오른쪽 child다.
      } else if (value > current.value) {
        current = current.right; 
      }
    }
    // while문을 나왔는데도 찾은 것이 없다면 undefined 반환한다.
    return undefined; 
  }

이진탐색트리의 성능

• 삽입 : $O(logn)$
• 탐색 : $O(logn)$

계속 이진으로 나눠서 찾는 로직이므로 $log_2n$의 시간복잡도가 나온다. 이처럼 이진탐색트리는 삽입과 탐색에서 빠르다.

하지만 위 이미지와 같이 한 쪽으로 쏠린 이진탐색트리에서 데이터를 삽입했을 때에는, $O(logn)$이 아니라 $O(n)$의 시간복잡도를 갖게 된다. 이런 경우에는 이진 트리나 이진탐색트리를 사용하지 않고 연결리스트 같은 다른 자료구조를 사용하는 것이 적절하다.