다익스트라(Dijkstra) 알고리즘

• 이번에 만드는 다익스트라 알고리즘은 ‘그래프’와 ‘우선순위 큐(이진 힙 버전)’ 개념을 이해하고 있어야 한다.
• 다익스트라 알고리즘은 그래프의 두 개의 정점 간에 최단 경로를 찾는 알고리즘이다.

기본 논리

1. 루프를 돌면서, 새로운 노드를 방문할 때마다 기록된 거리가 가장 짧은 노드부터 먼저 확인한다.
2. 방문할 노드로 이동한 후 각 노드에 인접한 이웃 노드들을 차례로 확인한다.
   • 각 이웃 노드에 대해 시작 노드에서부터 현재 보고 있는 노드까지 이어지는 전체 거리를 합산한다.
   • 현재 보고 있는 노드까지의 새로운 거리가 기존에 최단거리로 기록된 값보다 작으면, 새로운 더 짧은 거리를 저장한다.

가중 그래프(Weighted Graph)

• 다익스트라 알고리즘는 가중 그래프를 기반으로 한다. 예를 들어, A 장소(vertex1)와 B 장소(vertex2) 사이의 ‘거리’를 weight로서 간선에 추가해줘야 한다.

class WeightedGraph {
  constructor() {
    this.adjacencyList = {};
  }

  addVertex(vertex) {
    if (!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
  }

  addEdge(vertex1, vertex2, weight) {
    this.adjacencyList[vertex1].push({ node: vertex2, weight });
    this.adjacencyList[vertex2].push({ node: vertex1, weight });
  }
}

우선순위 큐(PriorityQueue)

• 단순히 배열로 우선순위 큐를 구현한 코드다. 성능이 더 좋은 이진 힙으로 구현한 우선순위 큐는 이진 힙 포스팅에서 확인할 수 있고, 그 PriorityQueue 클래스를 아래 코드와 교체하기만 하면 된다. 일단, 다익스트라에 집중하기 위해 우선순위 큐는 다음과 같이 간단히 구현하고 넘어간다.

class PriorityQueue {
  constructor() {
    this.values = [];
  }
  enqueue(val, priority) {
    this.values.push({ val, priority });
    this.sort();
  }
  dequeue() {
    return this.values.shift();
  }
  sort() {
    this.values.sort((a, b) => a.priority - b.priority);
  }
}

다익스트라 알고리즘 코드

// WeightedGraph 클래스 내부 메서드
  Dijkstra(start, finish) {
    // 위에서 만든 PriorityQueue 클래스로 nodes 인스턴스를 만들고, start를 추가한다. 
    const nodes = new PriorityQueue();
    nodes.enqueue(start, 0); 
    // distances 객체는 시작점부터 그 노드까지 최단 거리를 기록한다. 
    const distances = {};
    // previous 객체는 그 노드까지 최단거리로 경유해온 직전 노드를 기록한다. 
    const previous = {};
    // path 배열은 마지막에 return할 것이다.
    const path = []; 
    let smallest;
    // 다음과 같은 초기 상태를 만들기 위해 for문을 돌린다.
    // distances { A: 0, B: Infinity, C: Infinity, D: Infinity, E: Infinity, F: Infinity}
    // previous { A: null, B: null, C: null, D: null, E: null, F: null }
    for (const vertex in this.adjacencyList) {
      if (vertex === start) {
        distances[vertex] = 0;
        // 아래의 while문에서 처음에 nodes로부터 dequeue할 초깃값 추가하기
      } else {
        distances[vertex] = Infinity;
      }
      previous[vertex] = null;
    }
    
    // 무한 루프를 돌린다. 
    while (true) {
      // nodes 내부에서는 우선순위 정렬이 되어 있어 dequeue시 우선순위가 가장 높은(여기서는 최소 거리) 값을 주며, 그 값의 노드명을 smallest 변수에 재할당한다.
      smallest = nodes.dequeue().val;
      // dequeue한 값이 finish와 같으면 목적지에 도착한 것이므로,
      if (smallest === finish) {
        // return할 값을 아래의 while문을 통해 만들고 상위 while문을 break한다. 
        while (previous[smallest]) {
          path.push(smallest);
          smallest = previous[smallest];
        }
        break;
      }
      // dequeue한 값이 finish와 같지 않으면,
      else {
        // dequeue한 노드와 간선으로 이어진 노드들에 대하여 아래 과정의 반복문을 돌린다. 
        for (const neighbor in this.adjacencyList[smallest]) {
          const nextNode = this.adjacencyList[smallest][neighbor];
          // 시작점에서 현 노드까지 경유한 거리(distances[smallest])와 
          // 현 노드와 다음 노드 사이의 거리(nextNode.weight)를 합하여 최소거리 후보로 둔다.
          const candidate = distances[smallest] + nextNode.weight;
          const nextNeighbor = nextNode.node;
          // 시작점에서 다음 노드까지 가장 짧은 거리를 구하기 위해, 
          // 방금 만든 후보 값과 기존에 저장된 거리값을 비교하여, 후보 값이 더 작으면,
          if (candidate < distances[nextNeighbor]) {
            // 새로운 최소 거리 값으로 업데이트한다.
            distances[nextNeighbor] = candidate;
            // 다음 노드로 가기 위해 직전에 들린 노드를 기록한다. 
            previous[nextNeighbor] = smallest;
            // 다음 노드와 그곳까지 걸린 거리(priority)를 nodes에 넣는다.
            nodes.enqueue(nextNeighbor, candidate);
          }
        }
      }
    }
    return path.concat(smallest).reverse();
  }

코드 실행 결과

const graph = new WeightedGraph();
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.addVertex("D");
graph.addVertex("E");
graph.addVertex("F");

graph.addEdge("A", "B", 4);
graph.addEdge("A", "C", 2);
graph.addEdge("B", "E", 3);
graph.addEdge("C", "D", 2);
graph.addEdge("C", "F", 4);
graph.addEdge("D", "E", 3);
graph.addEdge("D", "F", 1);
graph.addEdge("E", "F", 1);

graph.Dijkstra("A", "E");

// ["A", "C", "D", "F", "E"]

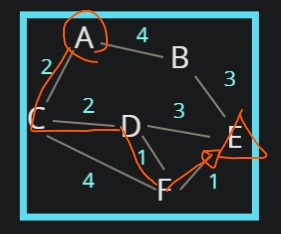
반복문에서 매 턴 마다 distances 객체에 기록된 값

{ A: 0, B: Infinity, C: Infinity, D: Infinity, E: Infinity, F: Infinity}
{ A: 0, B: 4, C: 2, D: Infinity, E: Infinity, F: Infinity }
{ A: 0, B: 4, C: 2, D: 4, E: Infinity, F: 6 }
{ A: 0, B: 4, C: 2, D: 4, E: 7, F: 6 }
{ A: 0, B: 4, C: 2, D: 4, E: 7, F: 5 }
{ A: 0, B: 4, C: 2, D: 4, E: 6, F: 5 }
{ A: 0, B: 4, C: 2, D: 4, E: 6, F: 5 }

반복문에서 매 턴 마다 previous 객체에 기록된 값

{ A: null, B: null, C: null, D: null, E: null, F: null }
{ A: null, B: 'A', C: 'A', D: null, E: null, F: null }
{ A: null, B: 'A', C: 'A', D: 'C', E: null, F: 'C' }
{ A: null, B: 'A', C: 'A', D: 'C', E: 'B', F: 'C' }
{ A: null, B: 'A', C: 'A', D: 'C', E: 'B', F: 'D' }
{ A: null, B: 'A', C: 'A', D: 'C', E: 'F', F: 'D' }
{ A: null, B: 'A', C: 'A', D: 'C', E: 'F', F: 'D' }

반복문에서 매 턴 마다 nodes에 enqueue, dequeue되는 과정 표시 

@nodes : PriorityQueue { values: [ Node { val: 'A', priority: 0 } ] }
@dequeue되는 smallest :  A
@nodes에 추가한 nextNeighbor :  B , candidate(priority) :  4
@nodes에 추가한 nextNeighbor :  C , candidate(priority) :  2

@nodes : PriorityQueue {
  values: [ Node { val: 'C', priority: 2 }, Node { val: 'B', priority: 4 } ]
}
@dequeue되는 smallest :  C
@nodes에 추가한 nextNeighbor :  D , candidate(priority) :  4
@nodes에 추가한 nextNeighbor :  F , candidate(priority) :  6

@nodes : PriorityQueue {
  values: [
    Node { val: 'B', priority: 4 },
    Node { val: 'D', priority: 4 },
    Node { val: 'F', priority: 6 }
  ]
}
@dequeue되는 smallest :  B
@nodes에 추가한 nextNeighbor :  E , candidate(priority) :  7

@nodes : PriorityQueue {
  values: [
    Node { val: 'D', priority: 4 },
    Node { val: 'F', priority: 6 },
    Node { val: 'E', priority: 7 }
  ]
}
@dequeue되는 smallest :  D
@nodes에 추가한 nextNeighbor :  F , candidate(priority) :  5

@nodes : PriorityQueue {
  values: [
    Node { val: 'F', priority: 5 },
    Node { val: 'E', priority: 7 },
    Node { val: 'F', priority: 6 }
  ]
}
@dequeue되는 smallest :  F
@nodes에 추가한 nextNeighbor :  E , candidate(priority) :  6

@nodes : PriorityQueue {
  values: [
    Node { val: 'F', priority: 6 },
    Node { val: 'E', priority: 7 },
    Node { val: 'E', priority: 6 }
  ]
}
@dequeue되는 smallest :  F

@nodes : PriorityQueue {
  values: [ Node { val: 'E', priority: 6 }, Node { val: 'E', priority: 7 } ]
}
@dequeue되는 smallest :  E