1. 우선순위 큐(Priority queue) 개요
지금까지 알던 큐(queue)라고 하면 먼저 들어가는 것이 먼저 나오는 선입선출(FIFO)이었지만, 우선순위 큐에서는 우선순위가 높은 데이터가 먼저 빠져나오게 된다. 그리고 이를 구현한 것이 힙!
우선순위 큐는 ADT(abstract data type)이고, 힙은 자료구조이다.
이제 씐나게 힙으로 우선순위 큐를 구현해보자 ₍₍ (ง ˙ω˙)ว ⁾⁾
2. 힙(Heap) 개요
최댓값 및 최솟값을 빠르게 찾아내기 위해 고안된 완전이진트리(complete binary tree)이다.
완전이진트리가 뭐였을까요?? 마지막 레벨의 경우 왼쪽부터 채워져있는 트리!
지난 시간에 정리한 보람이 있군! 뿌듯~~~
힙에서는 루트 노드의 우선순위가 가장 높다고 본다.
힙의 종류에는 2가지가 있다. 최대힙과 최소힙!
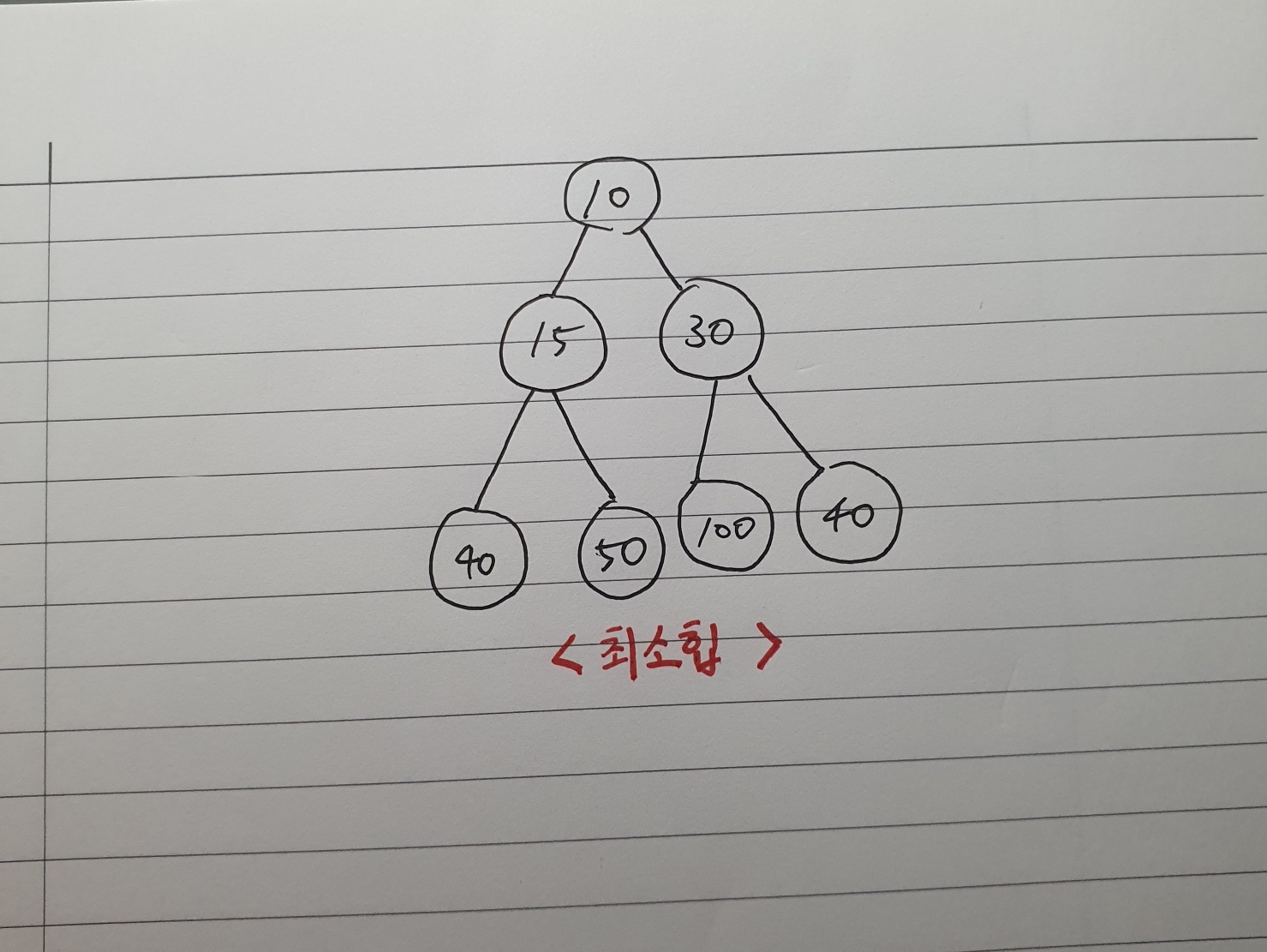
- 최대힙 : 부모노드의 키값이 자식노드의 키값보다 항상 크거나 같은 트리.
- 최소힙 : 부모노드의 키값이 자식노드의 키값보다 항상 작거나 같은 트리.
힙에서 대소관계는 부모노드와 자식노드 간에만 성립하고, 형제 사이에는 대소관계가 정해지지 않는다.
아래 그림은 최소힙의 예시이다.
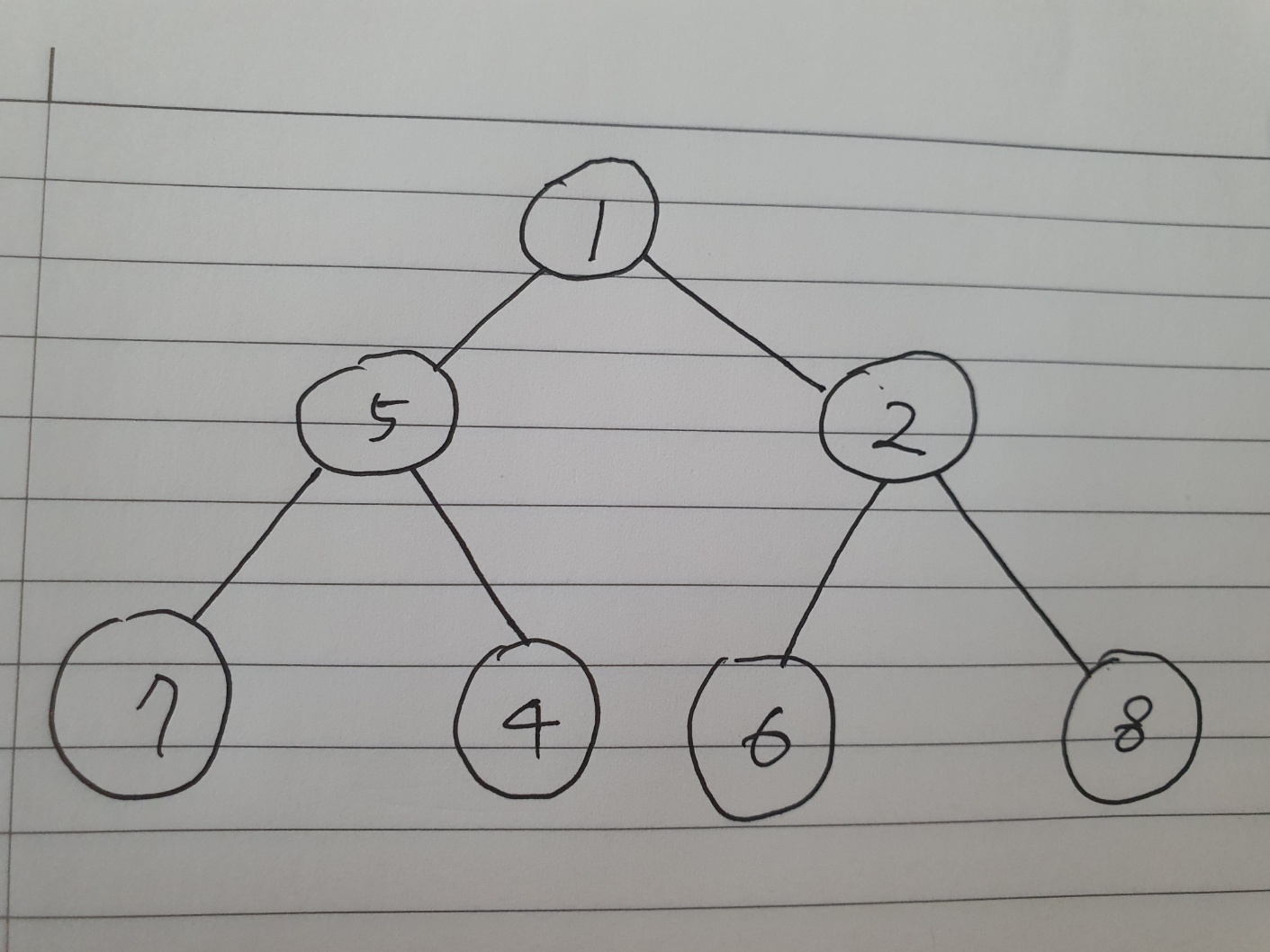
최소힙에서의 삽입(insert)
최소힙에 3의 값을 갖는 노드를 삽입한다고 가정해보자. 힙은 완전이진트리 기반이므로 왼쪽부터 뺴곡히 채워나가야 한다. 그림에서는 7의 왼쪽 자녀노드로 들어간다.
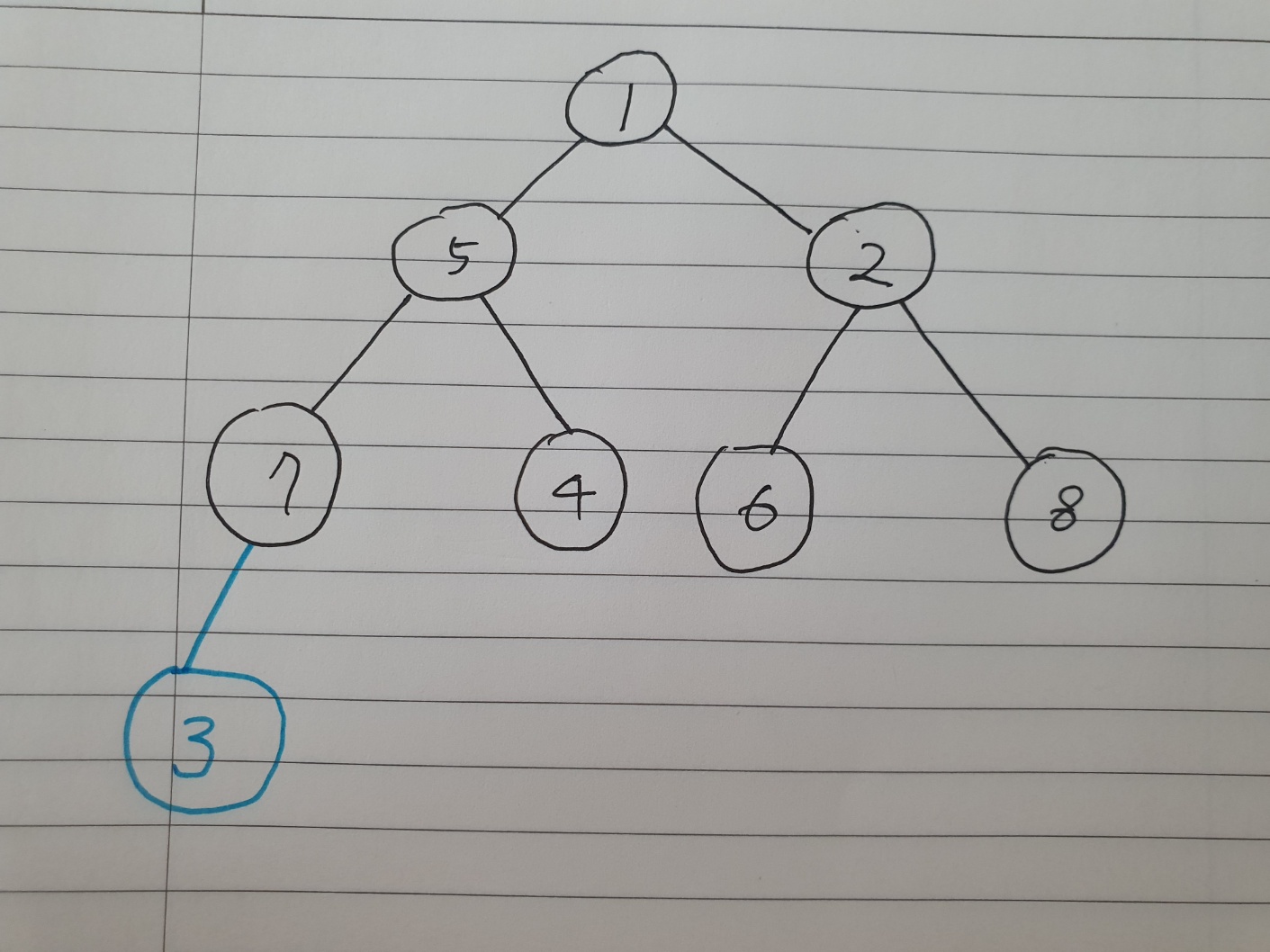
오잉 근데 최소힙인데 7 > 3이네? 부모 노드가 더 크면 최소힙이 아니지~~ 부모와 자식의 자리를 바꿔준다.
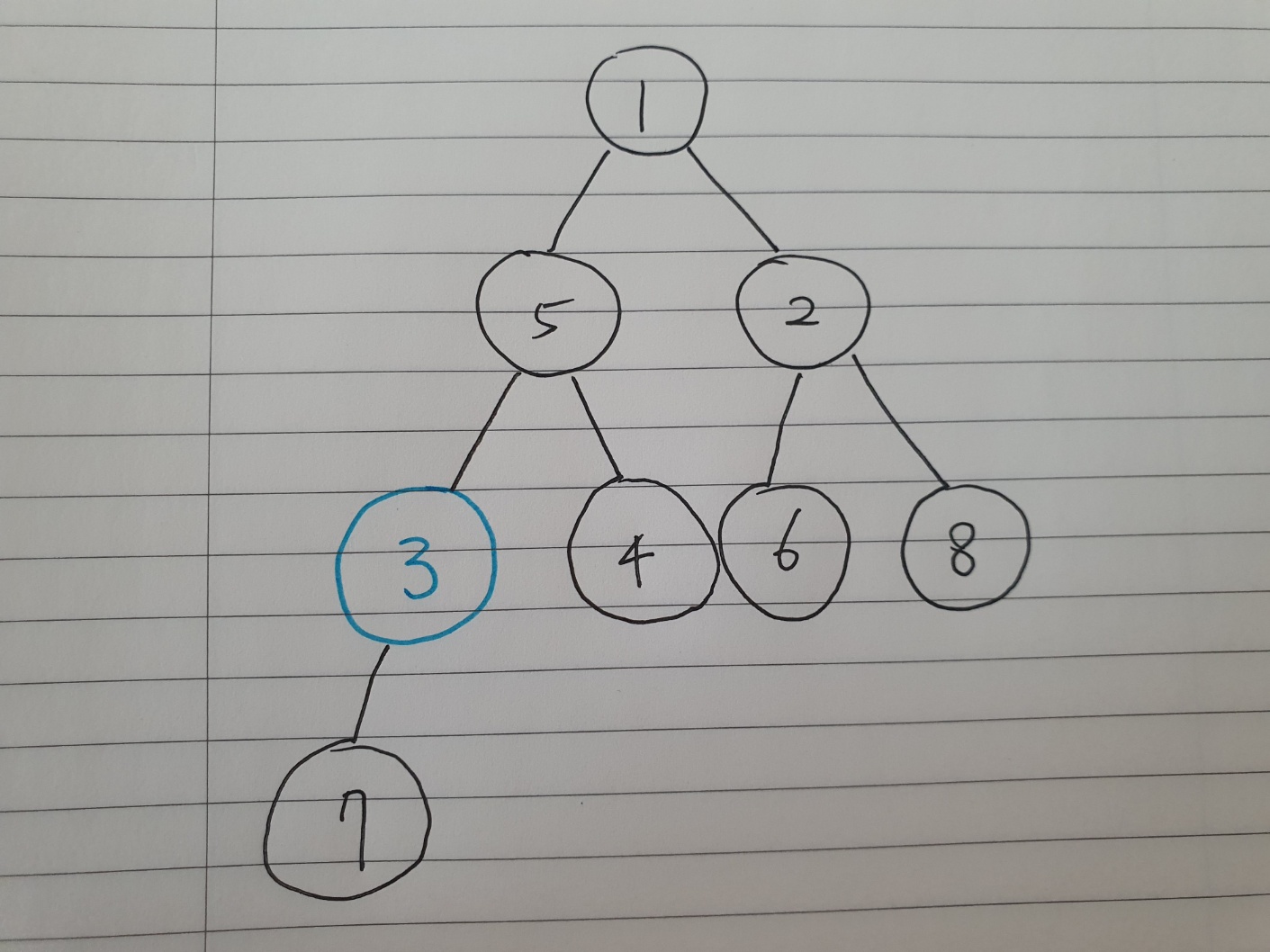
바꿨는데도 5 > 3이네? 5랑 3의 자리도 바꿔준다.
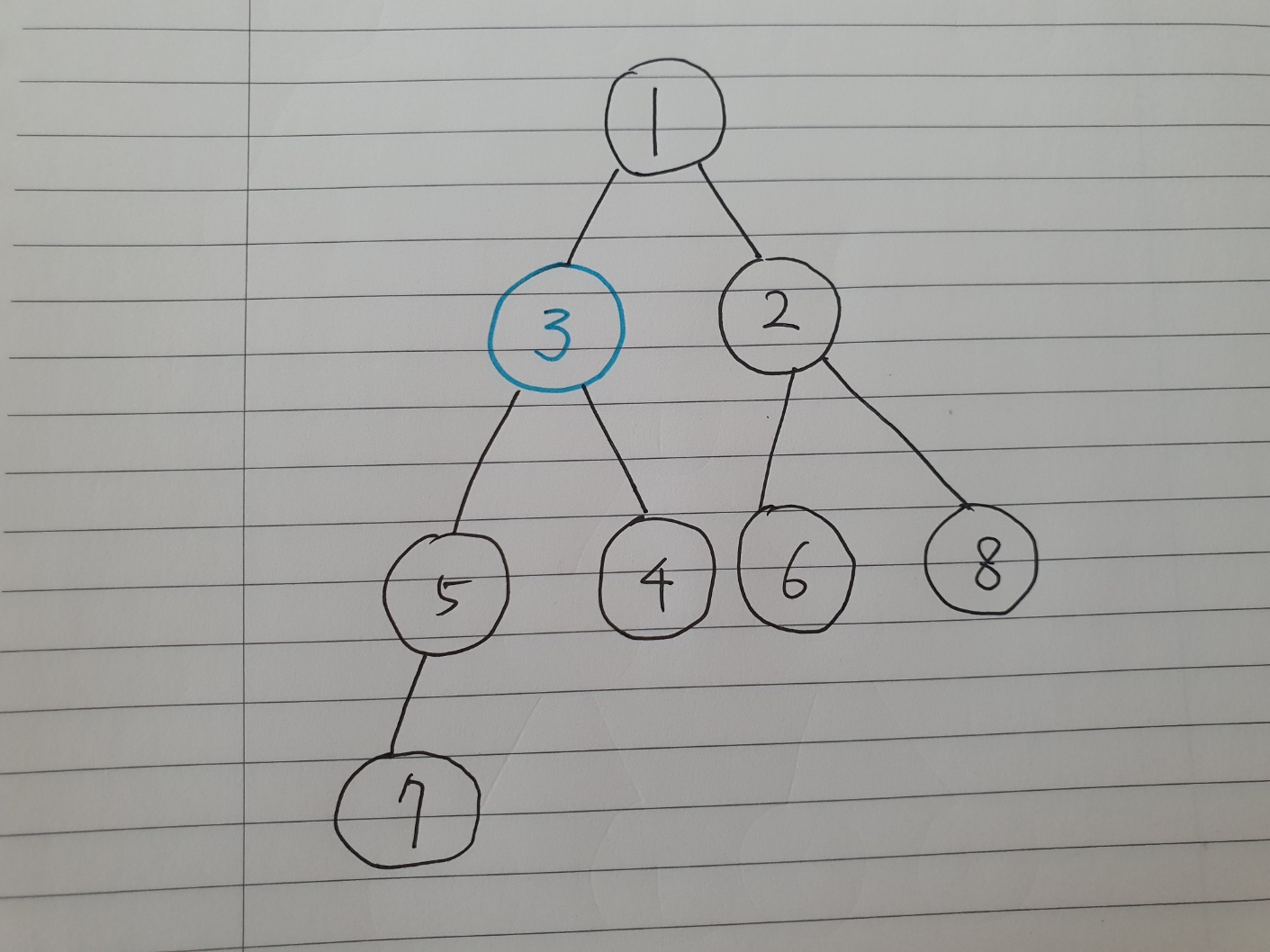
1 < 3이고 모든 노드에서 부모 노드 < 자식 노드이므로 마침내 최소힙이 된다!
최소힙에서의 삭제(delete)
우선순위 큐에서 삭제는 우선순위가 가장 높은 노드를 빼내는 것을 의미한다.
힙에서 우선순위가 가장 높은 노드는 루트노드이다.
고로 삭제한다? 루트노드를 없앤다는 뜻!
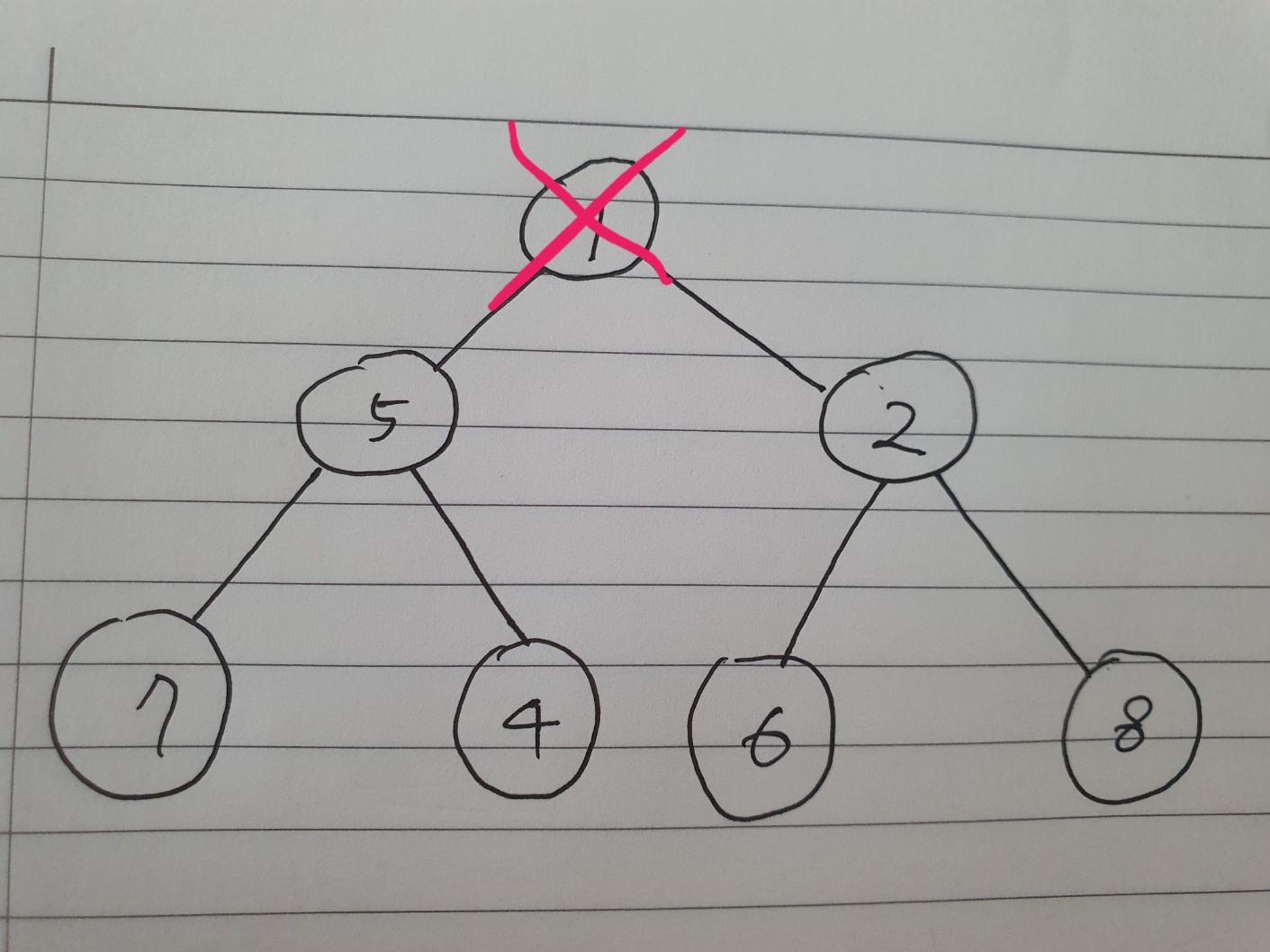
완전이진트리 기반이므로 리프노드 중 가장 오른쪽에 있는 노드인 8을 루트노드로 옮긴다.
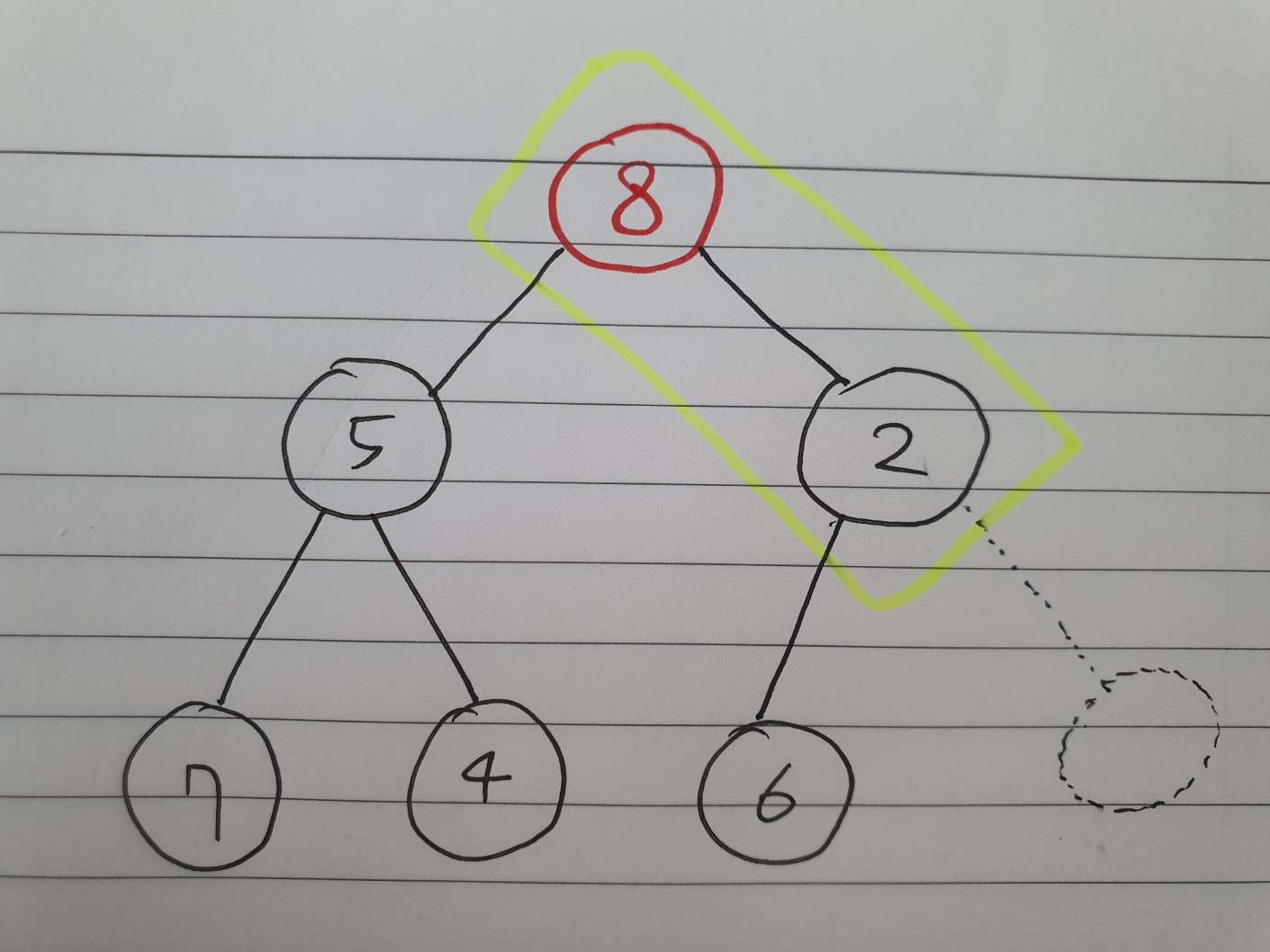
우리의 목표는 뭐다? 최소힙으로 만들기이다. 그런데 8의 자식노드가 전부 부모노드보다 우선순위가 높네? (숫자가 더 작네?) 그러므로 자식노드 중 우선순위가 더 높은 노드와의 비교를 계속 하며 자리를 바꿔줘야 한다. 그림에서는 5 > 2이므로 2의 우선순위가 더 높다.(최소힙이니까) 따라서 8과 2의 자리를 바꿔준다.
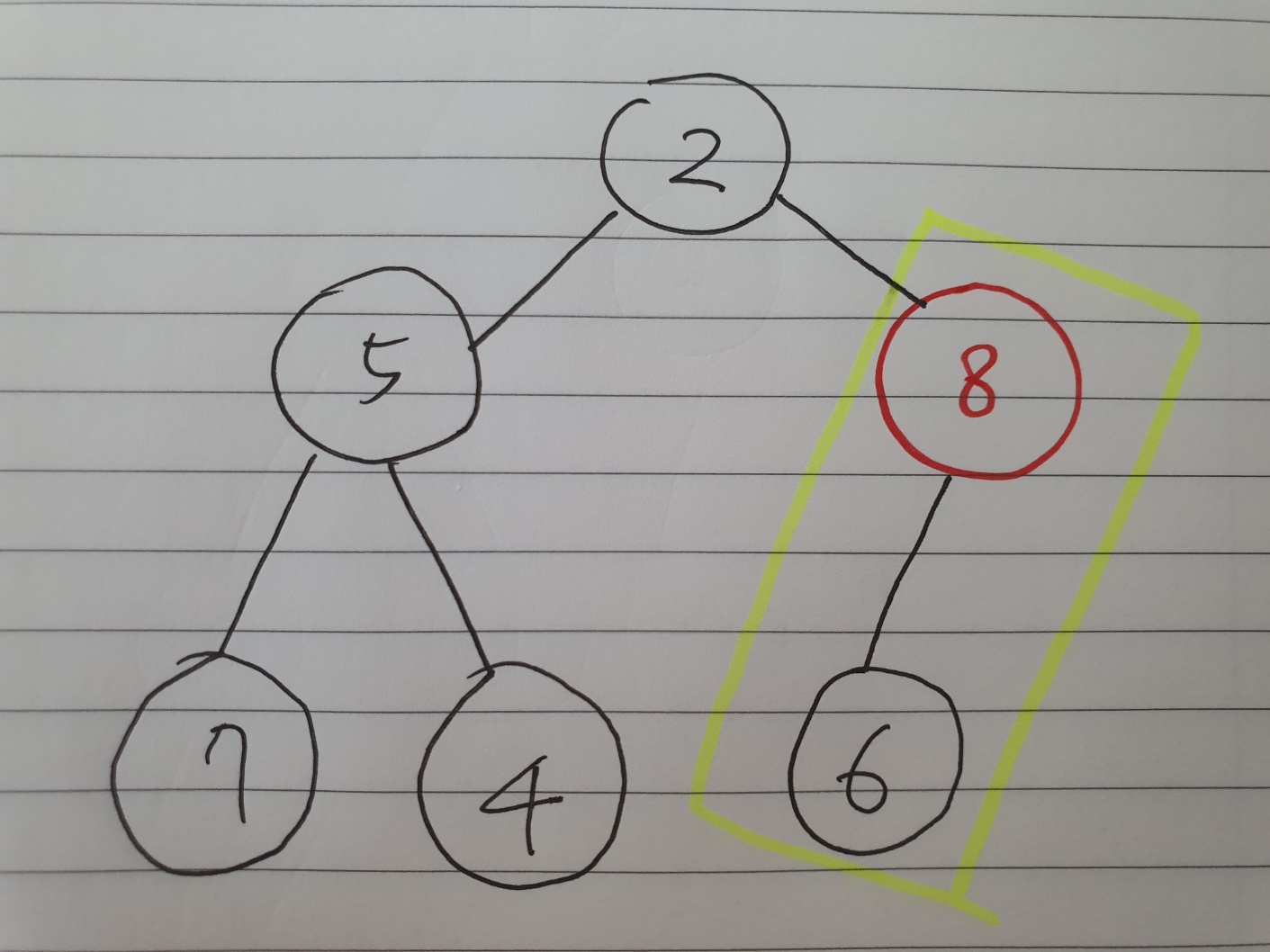
마찬가지로 8 > 6이므로 자리를 바꾼다.
삭제 후에도 최소힙으로 만들기 끝!
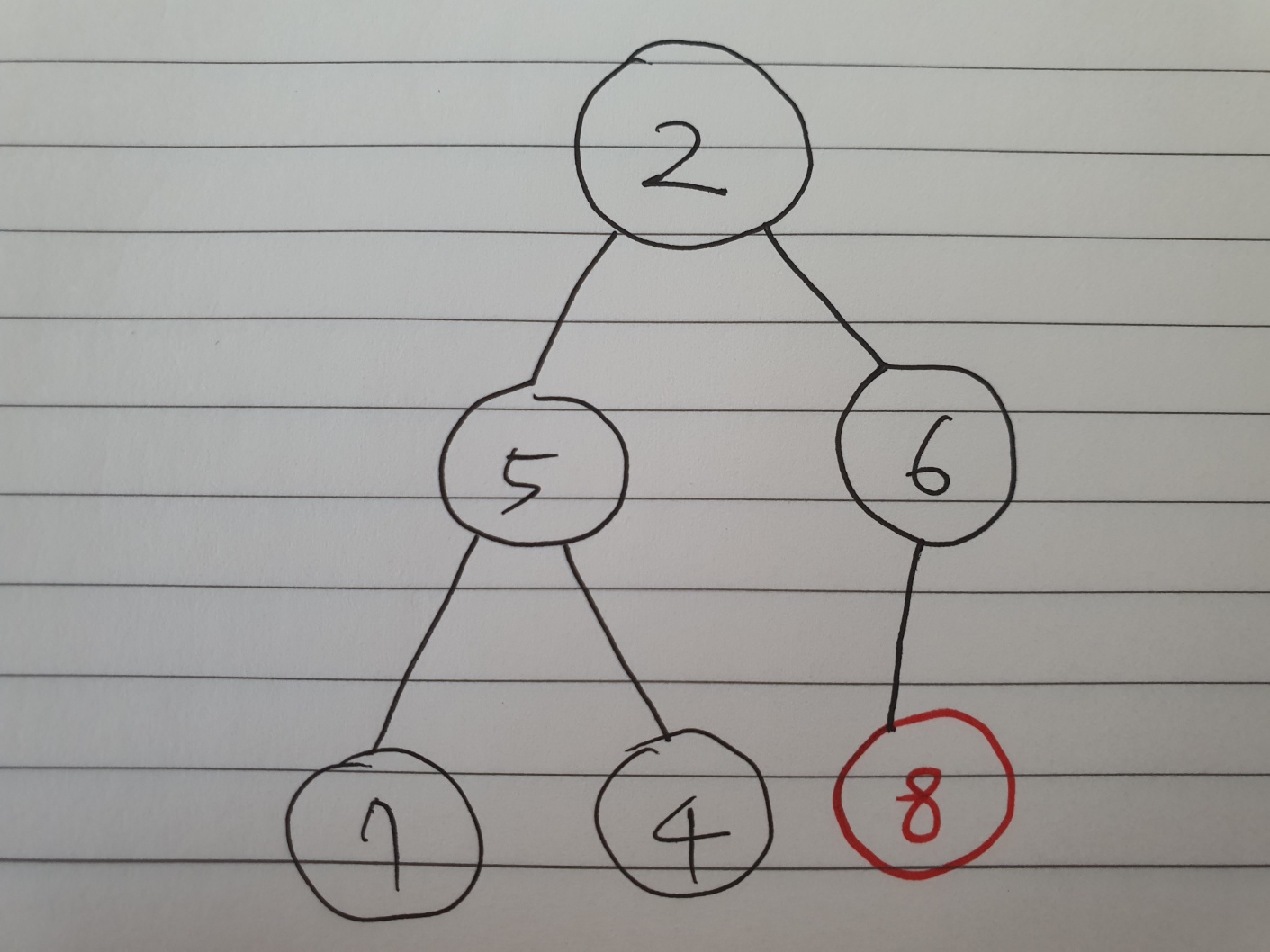
지금까지 최소힙을 예시로 봤지만, 최대힙의 경우에도 숫자가 클 수록 우선순위가 큰 것만 빼면 논리는 동일하다.
3. 우선순위 큐(Priority queue)를 힙(Heap)으로 구현할 때의 시간복잡도
삽입: O(logN)
자기자신을 부모 노드와 비교하여 swap함. 최악의 경우 루트노드까지 비교해야 함. 이때 swap하는 경로를 루트노드부터 거꾸로 내려와보면 비교해야 하는 대상 노드들의 수가 점점 절반씩 줄어드는 것을 알 수 있다.
삭제: O(logN)
마지막 리프노드를 루트노드 자리로 옮긴 후 최악의 경우 다시 리프노드로 내려와야 함. 이 때도 한 레벨 씩 내려올 때마다 비교해야할 대상 노드들의 수가 점점 절반씩 줄어든다.
배열과 연결리스트로 구현할 때와의 비교 ++ 아직 이해가 어려운 부분
다른 블로그들을 찾아보니 우선순위 큐를
- 순서 없는 배열
- 순서 없는 연결리스트
- 정렬된 배열
- 정렬된 연결 리스트
로 구현할 때의 시간복잡도도 함께 나와있다.
순서 없는 배열이나 순서 없는 연결리스트로 구현하면 삽입 시간 복잡도는 O(1)이고, 삭제 시간 복잡도는 O(N)이라고 한다.
그리고 정렬된 배열이나 정렬된 연결리스트로 구현하면 삽입 시간 복잡도는 O(N)이고, 삭제 시간복잡도는 O(1)이라고 한다.
힙으로 구현하면 시간복잡도가 왜 각각 O(logN)인지 이해가 되는데, 배열이나 연결리스트로 구현하면 왜 저런 시간복잡도가 나오는지 아직 도저히.. 모르겠다...
좀 더 실력을 연마하고 나서 꼭 !!! 다시봐야겠다. 다짐 !!
일단 지금은 힙으로 구현하면 시간복잡도가 O(logN)이기 때문에 최악의 상황에서도 배열/연결리스트보다 빠르며, 이러한 이유로 보통 우선순위 큐를 힙으로 구현한다는 정도만 이해하도록 하자!
다음시간에는 맵과 셋을 보는 걸루~~~ 화이팅 쟤스민!!
참고:
https://mjmjmj98.tistory.com/154
https://www.youtube.com/watch?v=P-FTb1faxlo
쉬운 코드
