[프로그래머스 0레벨] 연속된 수의 합

나의 코드

function solution(num, total) {
    const initial = [...Array(num)].map((v,i)=>i+total);
    let initialTotal = initial.reduce((s,v)=>s+=v,0);
      let counter = 0;
     while(initialTotal>total){
         initialTotal -= num;
         counter++;
     }
      return initial.map((v)=>v-counter);
  }

우선 원소의 개수는 문제에서 준 num과 동일하게 빈배열을 정의하고, map의 index를 활용하여 첫 원소가 total이 되도록한다.
이 상태에서 배열 내 원소의 총합을 구하여 initialTotal이라는 변수를 선언,
while문으로 initialTotal이 total과 같아질 때까지, initialTotal에서 한 바퀴 돌 때마다 num씩 빼며 while문이 몇 번 돌았는지 counter에 저장한다.
그리고 initial 배열의 각 원소에서 counter만큼 빼는 방식이다.

그런데 등차수열의 합공식을 이용하면 좀 더 간단하고 세련되게 표현할 수 있다.
등차수열의 합공식
n: 항의 개수
a: 첫 항
l: 마지막 항

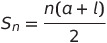
수식 입력 사이트:
http://www.sciweavers.org/free-online-latex-equation-editor

이 문제에도 적용하여 첫 항을 a로 두고 정리하면

function solution(num, total) {
    const a = (2 * total / num + 1 - num) / 2
    return Array(num).fill().map((_, i) => i + a)
}

이렇게도 가능하다.
total = a + (a + 1) + (a + 2) + ... + (a + num - 1)
= num * a + [ 1 + 2 + ... + num - 1]
= num * a + num * (num - 1) / 2
a로 정리하면
a = (2 * total / num + 1 - num) / 2
이므로 주어진 인자들로 첫항을 구할 수 있다.