[Algorithm] B+Tree

JAsmine_log·2024년 6월 7일

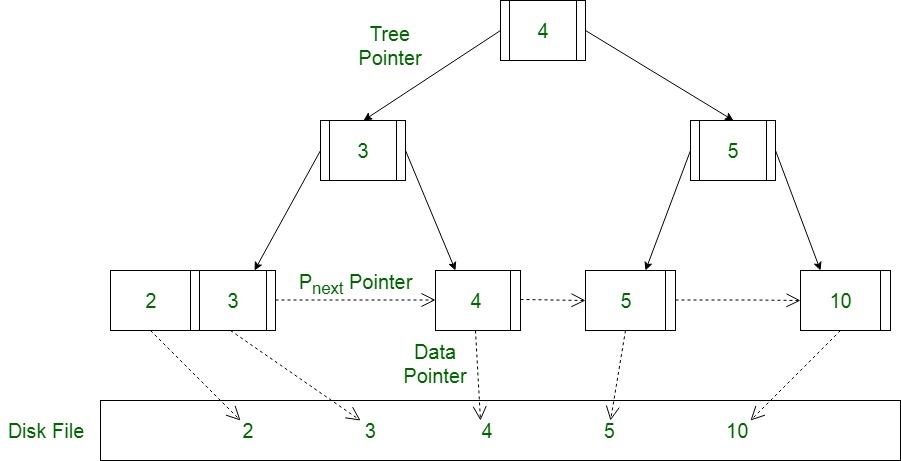
B-Tree

Concept

B+Tree 는 데이터 구조인 B-Tree를 변형한 것이다. B+Tree는 데이터 포인터를 리프 노드에만 저장한다. B+Tree는 2개의 다른 구조를 가진 Leaf Nodes는 Internal Nodes로 구성된다. Leaf Nodes는 검색 필드의 모든 값의 항목과 해당 레코드(또는 블록)가 가리키는 포인터를 갖는다. 또한, 레코드에 정렬된 접근을 제공을 위해서 서로 연결된다. 이에 반해 B+Tree의 Internal Nodes는 검색을 안내하며, 리프노드의 일부 검색 필드값이 반복된다. B+ 트리에서의 삭제는 검색, 삭제 및 균형 조정을 모두 포함한다.

Internal Nodes: n/2개의 레코드 포인터를 갖고 있지만, root노트에 대한 포인트는 없다
Leaf Nodes: n개의 포인터를 갖는다.

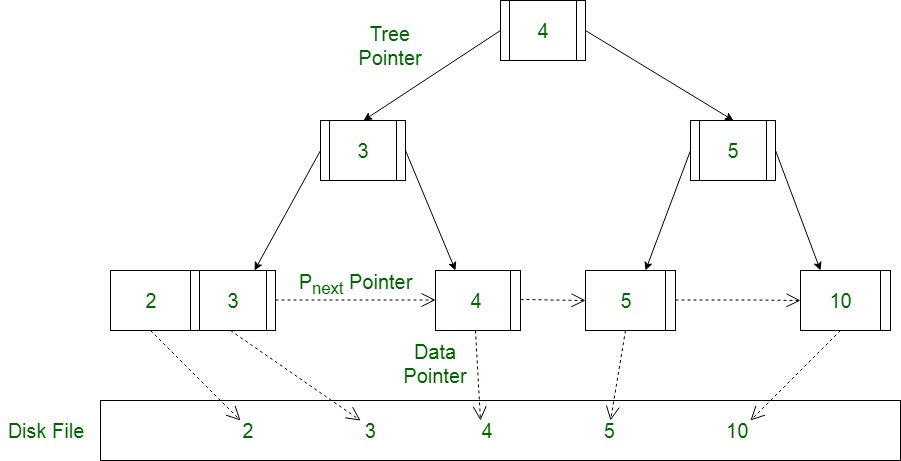
B+Tree The B+ tree is similar to the B-tree data structure in that it is a tree structure with a fixed number of keys per node, and it is balanced so that all leaf nodes are at the same level. However, in a B+ tree, all keys are stored in the leaf nodes, while the internal nodes only contain pointers to other nodes.

Characteristics

Balanced
Multiple keys per node
Multi-level
Ordered
All keys are stored in leaf nodes
Fan-out
Internal nodes have a higher fanout
Cache-friendly
Disk-oriented

Pros & Cons

Pros
- Faster data retrieval
- Support for range queries
- Sequential access is efficient
- Balanced structure
Cons
- Complex implementation
- Slower inserts and deletes
- Higher memory overhead
- Limited use cases

Application

Database indexing : 대규모 데이터베이스 인덱싱,
- Key = 테이블 인덱스, leaf node = 테이블의 실제 값
File systems : 많은 파일을 구성하고 저장,
- Key = 파일 이름, leaf node = 실제 파일 데이터에 대한 포인터 값
Operating systems : 가상 메모리 관리,
- Key = 베이지 번호, leaf node = 실제 물리적인 메모리 페이지의 포인터 값
Networking : 라우팅 정보를 저장하고 검색,
- Key=네트워크 주소, leaf node= 라우팅 경로 정보

Time Complexity of B+Tree:

Method	Time Complexity
Insert	O(log (h*bucketSize))
Delete	O(log (h*bucketSize))

Code

#include <bits/stdc++.h>

class Node {
public:
    std::vector<int> keys;
    std::vector<Node*> values;
    bool leaf;
    Node* next;

    Node(bool isLeaf) : leaf(isLeaf), next(nullptr) {}
};

class BPlusTree {
private:
    Node* root;
    int degree;

public:
    BPlusTree(int degree) : degree(degree) {
        root = new Node(true);
    }

    bool search(int key) {
        Node* current = root;
        while (!current->leaf) {
            int i = 0;
            while (i < current->keys.size()) {
                if (key < current->keys[i]) {
                    break;
                }
                i += 1;
            }
            current = current->values[i];
        }

        int i = 0;
        while (i < current->keys.size()) {
            if (key == current->keys[i]) {
                return true;
            }
            i += 1;
        }
        return false;
    }

    void insert(int key) {
        Node* current = root;
        if (current->keys.size() == 2 * degree) {
            Node* newRoot = new Node(false);
            root = newRoot;
            newRoot->values.push_back(current);
            split(newRoot, 0, current);
            insertNonFull(newRoot, key);
        } else {
            insertNonFull(current, key);
        }
    }

    void insertNonFull(Node* current, int key) {
        int i = 0;
        while (i < current->keys.size()) {
            if (key < current->keys[i]) {
                break;
            }
            i += 1;
        }

        if (current->leaf) {
            current->keys.insert(current->keys.begin() + i, key);
        } else {
            if (current->values[i]->keys.size() == 2 * degree) {
                split(current, i, current->values[i]);
                if (key > current->keys[i]) {
                    i += 1;
                }
            }
            insertNonFull(current->values[i], key);
        }
    }

    void split(Node* parent, int index, Node* node) {
        Node* newNode = new Node(node->leaf);
        parent->values.insert(parent->values.begin() + index + 1, newNode);
        parent->keys.insert(parent->keys.begin() + index, node->keys[degree - 1]);

        newNode->keys.insert(newNode->keys.end(), node->keys.begin() + degree, node->keys.end());
        node->keys.erase(node->keys.begin() + degree - 1, node->keys.end());

        if (!node->leaf) {
            newNode->values.insert(newNode->values.end(), node->values.begin() + degree, node->values.end());
            node->values.erase(node->values.begin() + degree, node->values.end());
        }
    }

    void stealFromLeft(Node* parent, int i) {
        Node* node = parent->values[i];
        Node* leftSibling = parent->values[i - 1];
        node->keys.insert(node->keys.begin(), parent->keys[i - 1]);
        parent->keys[i - 1] = leftSibling->keys[leftSibling->keys.size() - 1];
        if (!node->leaf) {
            node->values.insert(node->values.begin(), leftSibling->values[leftSibling->values.size() - 1]);
            leftSibling->values.pop_back();
        }
    }

    void stealFromRight(Node* parent, int i) {
        Node* node = parent->values[i];
        Node* rightSibling = parent->values[i + 1];
        node->keys.push_back(parent->keys[i]);
        parent->keys[i] = rightSibling->keys[0];
        if (!node->leaf) {
            node->values.push_back(rightSibling->values[0]);
            rightSibling->values.erase(rightSibling->values.begin());
        }
    }

    
    void remove(int key) {
        Node* current = root;
        bool found = false;
        int i = 0;
        while (i < current->keys.size()) {
            if (key == current->keys[i]) {
                found = true;
                break;
            } else if (key < current->keys[i]) {
                break;
            }
            i += 1;
        }
        if (found) {
            if (current->leaf) {
                current->keys.erase(current->keys.begin() + i);
            } else {
                Node* pred = current->values[i];
                if (pred->keys.size() >= degree) {
                    int predKey = getMaxKey(pred);
                    current->keys[i] = predKey;
                    removeFromLeaf(predKey, pred);
                } else {
                    Node* succ = current->values[i + 1];
                    if (succ->keys.size() >= degree) {
                        int succKey = getMinKey(succ);
                        current->keys[i] = succKey;
                        removeFromLeaf(succKey, succ);
                    } else {
                        merge(current, i, pred, succ);
                        removeFromLeaf(key, pred);
                    }
                }

                if (current == root && current->keys.size() == 0) {
                    root = current->values[0];
                }
            }
        } else {
            if (current->leaf) {
                return;
            } else {
                if (current->values[i]->keys.size() < degree) {
                    if (i != 0 && current->values[i - 1]->keys.size() >= degree) {
                        stealFromLeft(current, i);
                    } else if (i != current->keys.size() && current->values[i + 1]->keys.size() >= degree) {
                        stealFromRight(current, i);
                    } else {
                        if (i == current->keys.size()) {
                            i -= 1;
                        }
                        merge(current, i, current->values[i], current->values[i + 1]);
                    }
                }

                remove(key);
            }
        }
    }

    void removeFromLeaf(int key, Node* leaf) {
        leaf->keys.erase(std::remove(leaf->keys.begin(), leaf->keys.end(), key), leaf->keys.end());

        if (leaf == root || leaf->keys.size() >= std::floor(degree / 2)) {
            return;
        }

        Node* parent = findParent(leaf);
        int i = std::distance(parent->values.begin(), std::find(parent->values.begin(), parent->values.end(), leaf));

        if (i > 0 && parent->values[i - 1]->keys.size() > std::floor(degree / 2)) {
            rotateRight(parent, i);
        } else if (i < parent->keys.size() && parent->values[i + 1]->keys.size() > std::floor(degree / 2)) {
            rotateLeft(parent, i);
        } else {
            if (i == parent->keys.size()) {
                i -= 1;
            }
            merge(parent, i, parent->values[i], parent->values[i + 1]);
        }
    }

    int getMinKey(Node* node) {
        while (!node->leaf) {
            node = node->values[0];
        }
        return node->keys[0];
    }

    int getMaxKey(Node* node) {
        while (!node->leaf) {
            node = node->values[node->values.size() - 1];
        }
        return node->keys[node->keys.size() - 1];
    }

    Node* findParent(Node* child) {
        Node* current = root;
        while (!current->leaf) {
            int i = 0;
            while (i < current->values.size()) {
                if (child == current->values[i]) {
                    return current;
                } else if (child->keys[0] < current->values[i]->keys[0]) {
                    break;
                }
                i += 1;
            }
            current = current->values[i];
        }
        return nullptr;
    }

    void merge(Node* parent, int index, Node* pred, Node* succ) {
        pred->keys.insert(pred->keys.end(), succ->keys.begin(), succ->keys.end());
        pred->values.insert(pred->values.end(), succ->values.begin(), succ->values.end());
        parent->values.erase(parent->values.begin() + index + 1);
        parent->keys.erase(parent->keys.begin() + index);

        if (parent == root && parent->keys.size() == 0) {
            root = pred;
        }
    }

    void rotateRight(Node* parent, int index) {
        Node* node = parent->values[index];
        Node* prev = parent->values[index - 1];
        node->keys.insert(node->keys.begin(), parent->keys[index - 1]);
        parent->keys[index - 1] = prev->keys[prev->keys.size() - 1];
        if (!node->leaf) {
            node->values.insert(node->values.begin(), prev->values[prev->values.size() - 1]);
            prev->values.pop_back();
        }
    }

    void rotateLeft(Node* parent, int index) {
        Node* node = parent->values[index];
        Node* next = parent->values[index + 1];
        node->keys.push_back(parent->keys[index]);
        parent->keys[index] = next->keys[0];
        if (!node->leaf) {
            node->values.push_back(next->values[0]);
            next->values.erase(next->values.begin());
        }
    }

    void printTree() {
        std::vector<Node*> currentLevel;
        currentLevel.push_back(root);

        while (!currentLevel.empty()) {
            std::vector<Node*> nextLevel;

            for (Node* node : currentLevel) {
                std::cout << "[";
                for (int i = 0; i < node->keys.size(); ++i) {
                    std::cout << node->keys[i];
                    if (i < node->keys.size() - 1) {
                        std::cout << ", ";
                    }
                }
                std::cout << "] ";

                if (!node->leaf) {
                    nextLevel.insert(nextLevel.end(), node->values.begin(), node->values.end());
                }
            }

            std::cout << std::endl;
            currentLevel = nextLevel;
        }
    }
};

int main() {
    // create a B+ tree with degree 3
    BPlusTree tree(3);

    // insert some keys
    tree.insert(1);
    tree.insert(2);
    tree.insert(3);
    tree.insert(4);
    tree.insert(5);
    tree.insert(6);
    tree.insert(7);
    tree.insert(8);
    tree.insert(9);

    // print the tree
    tree.printTree(); // [4] [2, 3] [6, 7, 8, 9] [1] [5]

    // delete a key
    tree.remove(3);

    // print the tree
    tree.printTree(); // [4] [2] [6, 7, 8, 9] [1] [5]

    return 0;
}

Reference
[1] https://www.geeksforgeeks.org/introduction-of-b-tree/

JAsmine_log

Everyday Research & Development

이전 포스트

[AI] NLP_ BERT vs. GPT

다음 포스트