[Algorithm] Time Complexity (시간복잡도 )

JAsmine_log·2024년 2월 29일

Time Complexity & Space Complexity

컴퓨터사이언스에서는 문제를 해결하는 여러가지 알고리즘이 있는데, 어떤 것이 가장 최적인지 비교하기 위한 방법이 필요하다. 일반적으로 입력이 n일 때, 결과를 얻을 때까지의 연산시간이다.

기계와 configurations 과는 독립적
인풋에 대한 직접적인 관계를 보여줌
두 개의 알고리즘을 명확하게 구분할 수 있음

Time Complexity

컴퓨터과학에서 알고리즘의 시간복잡도는 입력을 나타내는 문자열 길이의 함수로서 작동하는 알고리즘을 취해 시간을 정량화하는 것이다. 알고리즘의 시간복잡도는 주로 빅-오 표기법(Big-O notation)을 사용하여 나타내며, Pan Bubilek의 빅-오 표기법은 계수와 낮은 차수의 항을 제외시키는 방법이다.
by wikipedia

Big-O notaion Time Complexity

Notation	Name
$O(1), O(constant)$	constant
$O(\log{10})$	double logarithmic
$O(\log{n})$	logarithmic
$O((log{n})^c)$ , c>1	polylogarithmic
$O(n^c)$ , 0<c<1	fractional power
$O(n)$	linear
$O(n\log*{n})$	nlog-starn
$O(n\log{n}=O(\log{n!})$	linearithmic, lolinear, quasilinear, nlogn
$O(n^2)$	quadratic
$O(n^c)$	polynomial or algeraic
$O(c^n)$	exponential
$O(n!)$	factorial

Big-O notation 비교

알고리즘 복잡도는 아래 그림과 같이 성능이 더 좋고, 나쁘게 비교될 수 있다.

General Time complexity grpah

Input Length	Worst Accepted Time Complexity	Usually type of solutions
10 -12	$O(N!)$	Recursion and backtracking
15-18	$O(2N * N)$	Recursion, backtracking, and bit manipulation
18-22	$O(2N * N)$	Recursion, backtracking, and bit manipulation
30-40	$O(2N/2 * N)$	Meet in the middle, Divide and Conquer
100	$O(N4)$	Dynamic programming, Constructive
400	$O(N3)$	Dynamic programming, Constructive
2K	$O(N2* log N)$	Dynamic programming, Binary Search, Sorting, Divide and Conquer
10K	$O(N2)$	Dynamic programming, Graph, Trees, Constructive
1M	$O(N* log N)$	Sorting, Binary Search, Divide and Conquer
100M	$O(N), O(log N), O(1)$	Constructive, Mathematical, Greedy Algorithms

Types of Time complexity

시간 복잡도는 다양한 표기법이 있는데, Big-O( $O$ ), Big-Omega( $\Omega$ ), Big-Theta( $\Theta$ )가 있다.

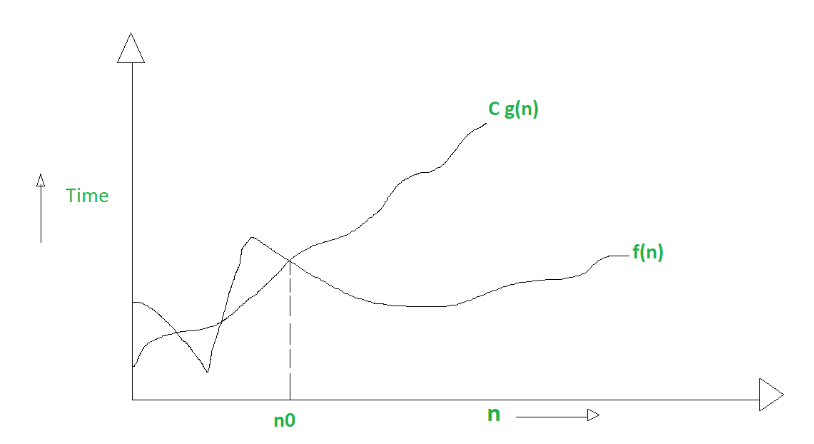
Big O notation ( $O$ ):
<=
upper bound
the most amount of time required
the worst case performanc
asymptotic upper bound
Mathematically – Big Oh is : $0 <= f(n) <= Cg(n) for all n >= n0$

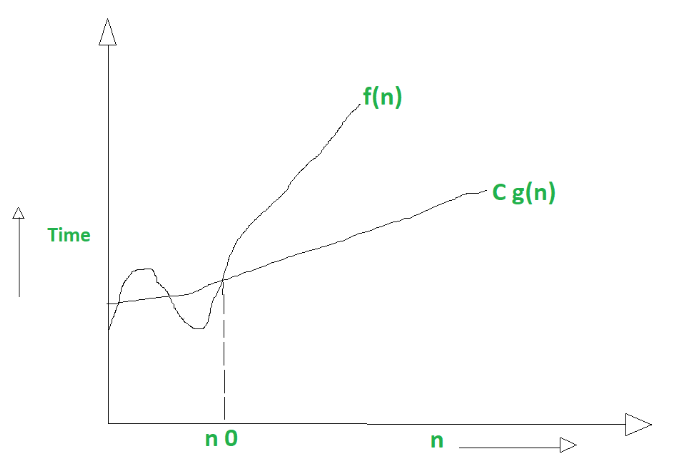
Big Omega notation ( $\Omega$ ) :
>=
lower bound
the least amount of time required
the most efficient way possible, i.e. best case
asymptotic lower bound
Mathematically – Big Omega is : $0 <= Cg(n) <= f(n) for all n >= n0$

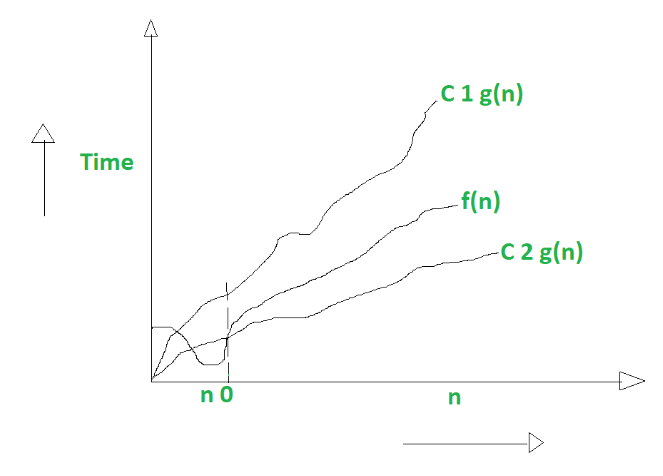
Big Theta notation ( $\Theta$ ) :
==
tightest bound
the best of all the worst case times
Mathematically – Big Theta is : $0 <= C2g(n) <= f(n) <= C1g(n) for n >= n0$