ECE (Expected Calibration Error)

범주: Machine Learning, Statistics

정의:

모델의 confidence와 실제 accuracy 차이를 평균적으로 측정한 값.

• $B_m$: 구간(bin)에 속한 예측들
• $acc(B_m)$: 실제 정확도
• $conf(B_m)$: 예측 확신도 평균

의미:

• 값이 0에 가까울수록 모델이 잘 calibrated.
• 값이 클수록 확신과 실제 성능이 불일치.

Key Idea:

Classification 모델 평가 시 정확도(accuracy)만 보는 대신 calibration도 함께 봐야 함.

"예측 확률과 실제 빈도의 차이"라는 점에서 통계적 측도(statistical measure)이지만,
주로 ML에서 calibration 성능 평가를 위해 제안된 지표.

Application

ECE에서 bin은 "confidence 구간"을 의미
모델이 출력한 확률(confidence)을 일정하게 나눈 구간에서 평균 정확도와 평균 확신도 $f$를 비교

• bin은 "confidence 구간"을 나눠 샘플들을 모아두는 바구니 역할.
• 각 bin에서 평균 확신도와 실제 정확도의 차이를 계산 → 전체 ECE는 이를 가중합한 값.
• 이 과정을 통해 모델이 자신감 있게 말한 것과 실제 맞춘 비율의 일치여부를 확인 가능

bin의 개념

예측 확률(0~1)을 여러 개의 구간으로 분할
예를 들어, 0~1 사이를 10개의 bin으로 나누면:

• bin1: [0.0 ~ 0.1)
• bin2: [0.1 ~ 0.2)
• …
• bin10: [0.9 ~ 1.0]

각 예측 샘플은 자신이 가진 확률(confidence)에 따라 해당 구간(bin)에 들어감.

쉬운 예시

예를 들어, 이진 분류 모델이 있고 5개 샘플에 대해 아래와 같이 예측했다고 가정:

샘플	모델 예측 확률 (positive일 확률)	실제 라벨
A	0.9	1
B	0.8	1
C	0.75	0
D	0.6	1
E	0.2	0

• bin 구간을 0.1 단위로 나눈다고 하면:

  • 샘플 A, B, C → bin [0.7~0.9)
  • 샘플 D → bin [0.6~0.7)
  • 샘플 E → bin [0.2~0.3)

bin 안에서의 비교

• bin [0.7~0.9):

  • 평균 confidence = (0.9+0.8+0.75)/3 = 0.82
  • 실제 정확도 = 2/3 ≈ 0.67 (라벨 1이 2개)
  • 차이 = |0.82 - 0.67| = 0.15

• bin [0.6~0.7):

  • confidence = 0.6
  • accuracy = 1/1 = 1.0
  • 차이 = |0.6 - 1.0| = 0.4

• bin [0.2~0.3):

  • confidence = 0.2
  • accuracy = 0/1 = 0.0
  • 차이 = |0.2 - 0.0| = 0.2

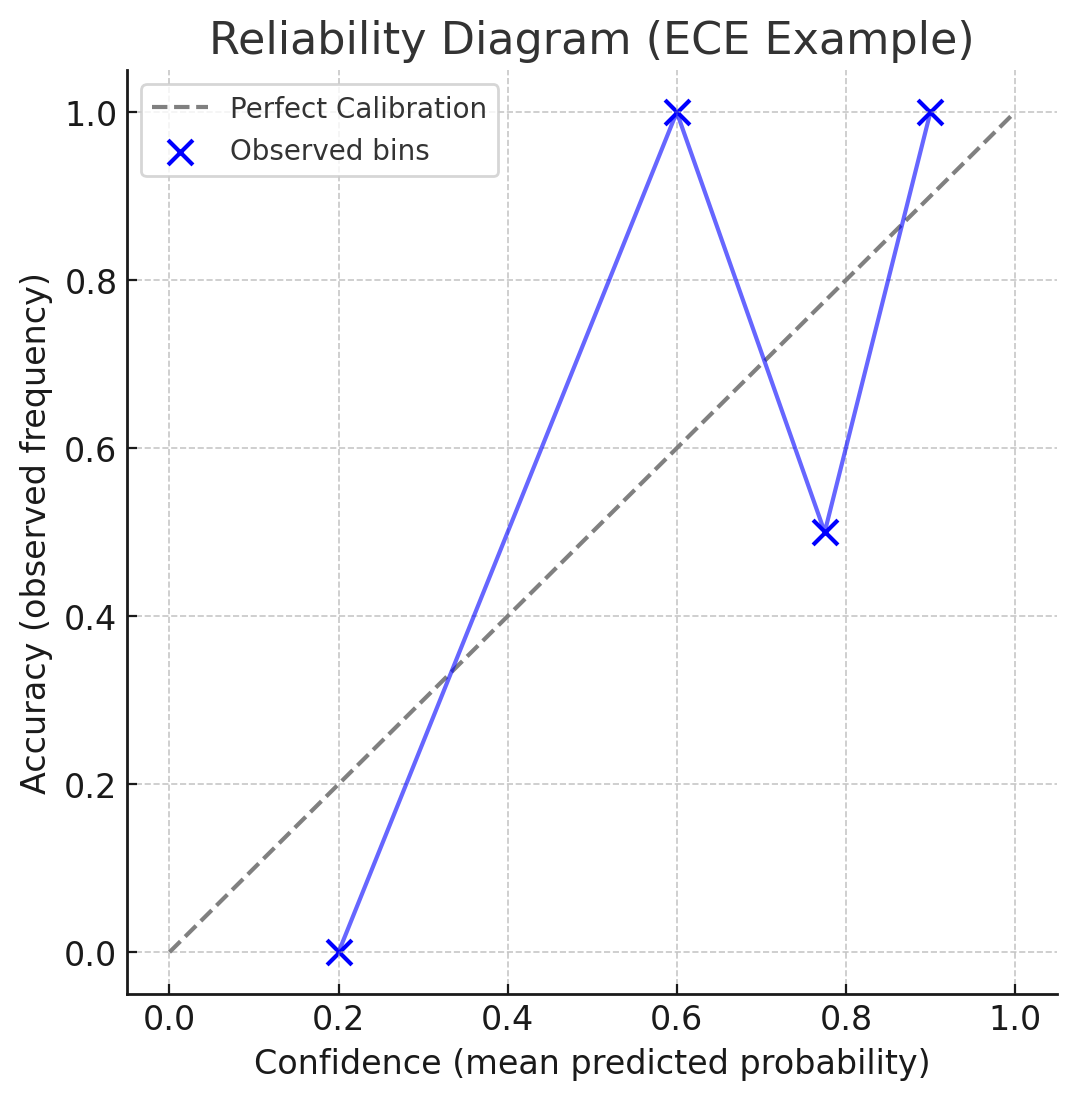
• 회색 점선(대각선): 모델이 완벽하게 calibrated 된 경우 (confidence와 accuracy가 항상 일치).
• 파란 점: 실제 bin 별 평균 confidence vs accuracy.
• 파란 선: bin들을 이어서 본 모델의 calibration 경향.