Temperature τ

Softmax와 연계하여 생각해보자

📐 Softmax + Temperature 식

• 어떤 점수 집합이든, temperature τ가 크든 작든 → 항상 합은 1

• softmax는 단순히 “점수 리스트”를 “확률 분포(합=1)”로 바꿔주는 함수

• temperature는 그 분포의 뾰족함 정도만 바꾸는 역할

• $z_i$: 점수 (logit)

• $\tau$: temperature

• 작은 $\tau$ → 분포가 뾰족

• 큰 $\tau$ → 분포가 평평

예제

• $\tau$는 온도와 비례

• 아이스크림 맛의 점수

  • 딸기맛 점수 = 10점 (제일 좋아함)
  • 초코맛 점수 = 9점
  • 바닐라맛 점수 = 1점

• softmax = 어떤 아이스크림 맛을 고를지에 대한 확률 분포로 변환

  • softmax는 이 점수를 확률로 바꿔서 “어떤 맛을 고를지” 결정
  • 여기서 temperature τ가 개입

$\tau = 1$ (보통)

• 대략 계산하면:

  • 딸기 ≈ 0.73
  • 초코 ≈ 0.27
  • 바닐라 ≈ 0.0001

→ 점수 차이를 그대로 반영.

$\tau = 0.5$ (차갑게, 샤프해짐)

• 딸기 ≈ 0.999
• 초코 ≈ 0.001
• 바닐라 ≈ 0

→ 거의 무조건 딸기만 고름.

$\tau = 10$ (뜨겁게, 스무딩됨)

• 딸기 ≈ 0.39
• 초코 ≈ 0.35
• 바닐라 ≈ 0.26

→ 결과가 거의 비슷하게 섞여서 나옴.

핵심 요약

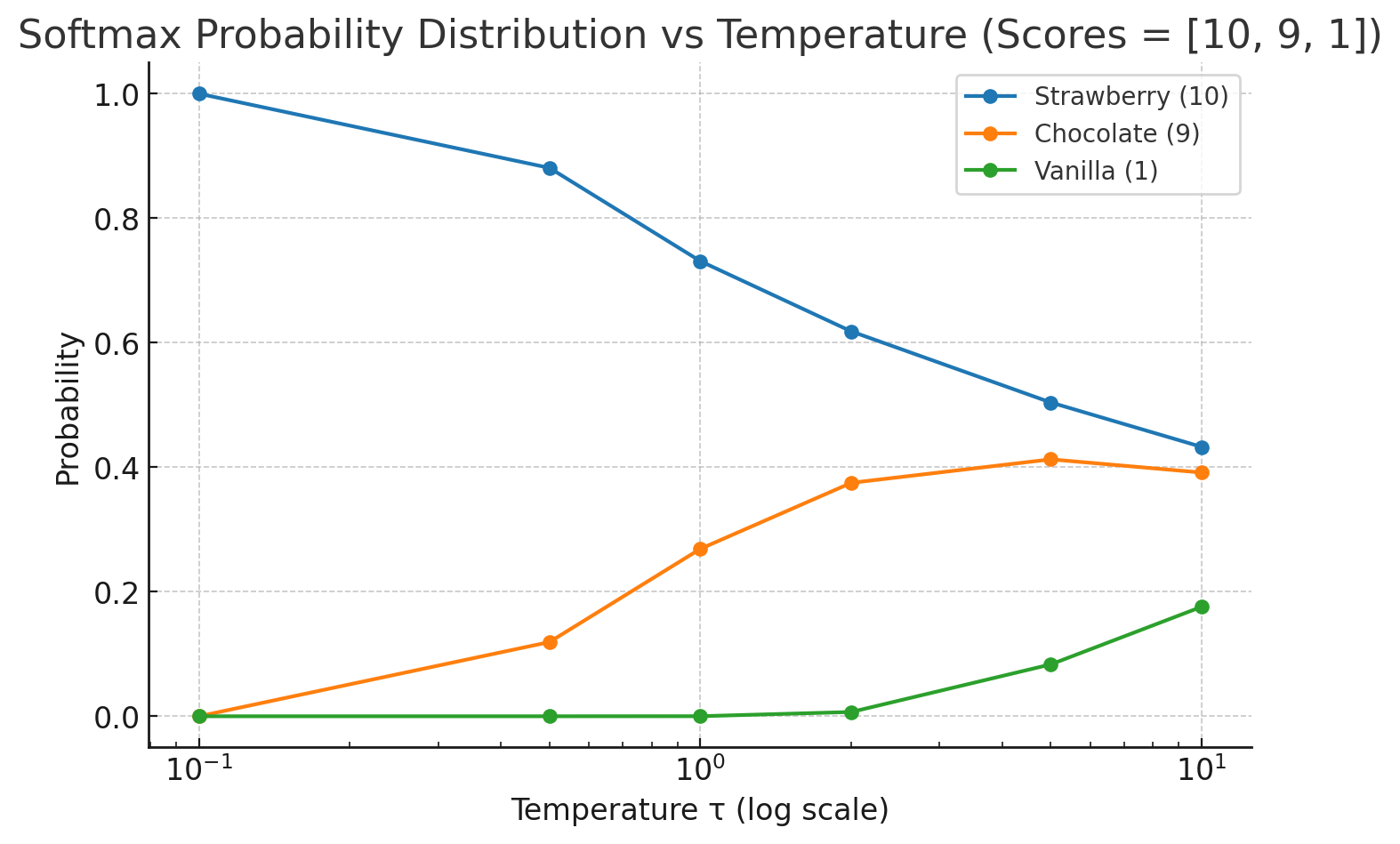
• $\tau \downarrow$ → 한 선택에 “몰빵” (확신 강해짐).
• $\tau \uparrow$ → 모든 선택을 비슷하게 (불확실해짐).