[Coding] 연속 펄스 부분 수열의 합

첫 코딩테스트를 봤다.

코딩테스트에 카데인 알고리즘을 이용한 해당 문제와 다른 문제를 선택하는 것이 나왔는데, 솔직히 신입 개발자로 지원하는건데 이렇게 어려운 문제가 나올줄은 몰랐다. 처음 알게된 개념이지만 그래도 카데인 알고리즘이 궁금할 때 찾아보면 좋을 것 같아서 기록한다.

Platform

programmers

Description

어떤 수열의 연속 부분 수열에 같은 길이의 펄스 수열을 각 원소끼리 곱하여 연속 펄스 부분 수열을 만들려 합니다. 펄스 수열이란 [1, -1, 1, -1 …] 또는 [-1, 1, -1, 1 …] 과 같이 1 또는 -1로 시작하면서 1과 -1이 번갈아 나오는 수열입니다.
예를 들어 수열 [2, 3, -6, 1, 3, -1, 2, 4]의 연속 부분 수열 [3, -6, 1]에 펄스 수열 [1, -1, 1]을 곱하면 연속 펄스 부분수열은 [3, 6, 1]이 됩니다. 또 다른 예시로 연속 부분 수열 [3, -1, 2, 4]에 펄스 수열 [-1, 1, -1, 1]을 곱하면 연속 펄스 부분수열은 [-3, -1, -2, 4]이 됩니다.
정수 수열 sequence가 매개변수로 주어질 때, 연속 펄스 부분 수열의 합 중 가장 큰 것을 return 하도록 solution 함수를 완성해주세요.

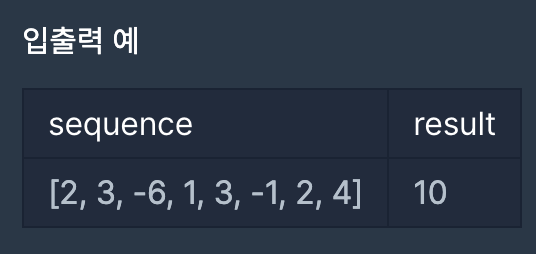
주어진 수열의 연속 부분 수열 [3, -6, 1]에 펄스 수열 [1, -1, 1]을 곱하여 연속 펄스 부분 수열 [3, 6, 1]을 얻을 수 있고 그 합은 10으로서 가장 큽니다.

Solution

class Solution {
    public long solution(int[] sequence) {
        return Math.max(
	        // 펄스 수열이 [1, -1, 1, -1, ...] 시작
            maxSubarraySumWithPulse(sequence, true),
            // 펄스 수열이 [-1, 1, -1, 1, ...] 시작
            maxSubarraySumWithPulse(sequence, false) 
        );
    }

    private long maxSubarraySumWithPulse(int[] sequence, boolean startWithPositive) {
	    // 현재까지의 최대 부분 배열 합
        long maxEndingHere = 0; 
        // 전체 최대 부분 배열 합
        long maxSoFar = Integer.MIN_VALUE;
        // 현재 인덱스의 펄스 수열 값
        int multiplier = startWithPositive ? 1 : -1;

        for (int num : sequence) {
            maxEndingHere += num * multiplier;
            maxSoFar = Math.max(maxSoFar, maxEndingHere);
            maxEndingHere = Math.max(maxEndingHere, 0);
            // 펄스 수열 값 반전
            multiplier *= -1;  
        }

        return maxSoFar;
    }
}

Other solution

TIL - 카데인 알고리즘(Kadane's Algorithm)

카데인 알고리즘(Kadane's Algorithm)은 주어진 수열에서 연속된 요소들의 최대 합을 효율적으로 찾는 방법입니다. 이 알고리즘은 한 번의 순회만으로 최대 부분 배열의 합을 찾을 수 있어 시간 복잡도는 O(n)입니다.

카데인 알고리즘의 기본 아이디어

배열을 순회하면서, 각 요소에서 끝나는 최대 부분 배열의 합을 계산합니다.
이 합은 이전 요소에서 끝나는 최대 부분 배열에 현재 요소를 더하는 것과 현재 요소만을 포함하는 것 중 큰 값입니다.
전체 배열을 순회하면서 최대 부분 배열의 합을 업데이트합니다.

class Solution {
    public int maxSubArray(int[] nums) {
        int maxEndingHere = nums[0]; // 현재 요소에서 끝나는 최대 부분 배열의 합 초기화
        int maxSoFar = nums[0]; // 전체 최대 부분 배열의 합 초기화

        for (int i = 1; i < nums.length; i++) {
            maxEndingHere = Math.max(nums[i], maxEndingHere + nums[i]);
            maxSoFar = Math.max(maxSoFar, maxEndingHere);
        }

        return maxSoFar;
    }
}