[kotlin fp] 펑터(Functor)

dante Yoon·2022년 4월 18일

functional programming kotlin

kotlin

목록 보기

9/9

코틀린으로 배우는 함수형 프로그래밍을 읽고 정리한 내용입니다.

이번 포스트부터는 난이도가 좀 상승한다.

펑터란

함수형 프로그래밍은 범주론이라는 수학적 원리를 토대로 만들어졌는데, 범주론에는 다양한 수학적 개념들이 존재한다. 그리고 함수형 언어에서는 증명된 개념들의 구현체를 만들어 제공한다.

각 구현체는 쓰임새와 사용법이 다르고, 어떤 행위를 정의한 타입 클래스의 인스턴스로 작성된다. 여기서 타입 클래스는 코틀린에서 인터페이스로 구현된다.

그래서 펑터란?

펑터(Functor)는 매핑할 수 있는 것 (can be mapped over)이라는 행위를 선언한 타입 클래스를 말한다. 여기서 매핑할 수 있는 것이라는 동작은 리스트의 map과 동일하다.

펑터에 대해 그림으로 설명해 놓은 글이 있어 먼저 공유하고 포스팅을 이어가겠다.

코틀린 리스트의 map 함수의 타입은 다음과 같다.

fun <T, R> Iterable<T>.map(f: (T) -> R): List<R>

map 함수는 객체가 가진 T의 값을 f 함수에 적용하여 R타입의 값을 얻은 후, 이 값을 다시 List 객체 안에 넣은 List<R>을 반환하는 함수다.

여기서 Iterable과 List는 각각 T와 R 타입을 담을 수 있는 박스라고 생각해볼 수 있다. map의 행위를 박스에 있는 물건을 꺼내 변환 시키는 과정과 비유해서 보면, 다음과 같다. (그림은 앞서 공유한 글에서 캡처하였다.)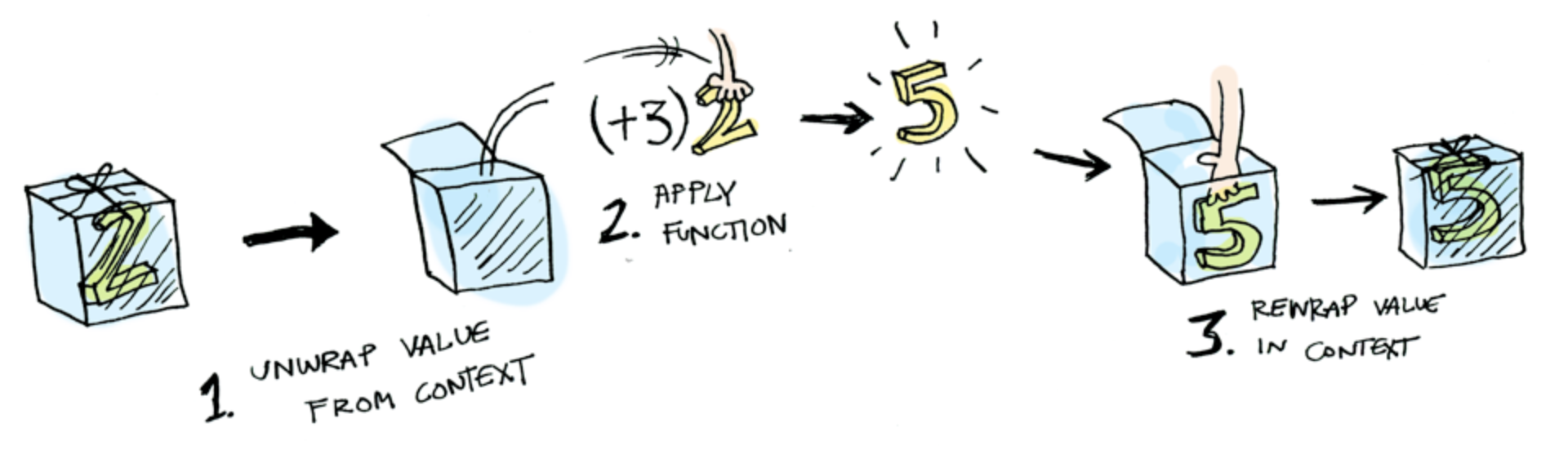

펑터는 리스트 같은 컨테이너형 타입의 값을 꺼내서 입력받은 함수를 적용후 함수의 결과값을 컨테이터형 타입에 넣어서 반환하는 행위를 선언한 타입 클래스를 의미한다.

타입 클래스란

A typeclass is a sort of interface that defines some behavior.

펑터 자체는 추상화된 타입 클래스이기 때문에 List<Int>와 같이 컨테이너 타입이 가진 구체적인 타입까지 포함해서 정의하지 않는다는 것을 주의한다. 펑터는 List<T>와 같이 일반화된 타입을 가진다.

따라서 한개의 타입 매개변수를 받는 타입 생성자(type constructor)이다.

만약 타입 매개변수, 타입 생성자와 같은 용어에 아직 익숙하지 않다면 다음 포스팅을 참고하자.

단테 - 함수형 타입 시스템

펑터 선언하기

펑터를 직접 만들고 활용해보자. 펑터는 map 연산을 추상화 한다.

interface Functor<out A> {
  fun <B> fmap(f: (A) -> B): Functor<B>
}

fmap 함수에서 Functor<B>타입을 반환한다면 오버라이드 하는 클래스에서 컨테이너형 타입으로 바꾸어 반환한다.

fmap함수는 입력받은 f 함수를 사용해 A값을 B로 변환한 후, 펑터에 담아서 Functor<B>로 반환한다.

메이비 펑터 만들기

Maybe는 어떤 값이 있을 수도 있고 없을 수도 있는 컨테이너형 타입이다.
어떤 함수의 반환 값을 메이비로 선언하면, 함수의 실패 가능성을 포함할 수 있어 불필요한 if else를 통한 널 처리나 예외를 피할 수 있다.

코틀린에서는 널 처리가 가능하기 때문에 메이비와 같은 타입을 지원하지 않아 다음과 같이 직접 구현했다.

sealed class Maybe<out A>: Functor<A> {
  abstract override fun toString(): String
  
  abstract override fun <B> fmap(f: (A) -> B): Maybe<B>
}

Maybe를 펑터로 만들기 위해서 Functor 타입 클래스의 인스턴스로 선언했다. 여기서 인스턴스로 선언했다는 말은 객체지향 프로그래밍의 상속을 의미하며 함수형 프로그래밍에서 타입 클래스를 다룰 때 사용되는 용어이다.

fmap 함수는 펑터에 정의된 fmap과 동일하지만 반환하는 값의 타입만 Maybe로 변환한다.

Maybe의 값이 있는 상태와 없는 상태의 구현 클래스(implementation class)를 작성해보자.

Just

data class Just<out A>(val value: A): Maybe<A>() {
  override fun toString(): String = "Just($value)"
  override fun <B> fmap(f: (A) -> B): Maybe<B> = Just(f(value))
}

Just는 값을 반드시 포함한 상태다. 따라서 생성자를 통해서 포함된 값을 입력받는다. fmap 함수는 Just가 가진 값을 함수 f에 적용해서 반환하고 다시 컨테이너 타입인 Just에 넣어서 반환한다.

Nothing

object Nothing: Maybe<kotlin.Nothing>() {
  override fun toString(): String = "Nothing"
  
  override fun <B> fmap(f: (kotlin.Nothing) -> B): Maybe<B> = Nothing
}

Nothing은 값이 없는 상태다. 값을 포함하지 않기 때문에 생성자로 부터 어떤 입력도 받지 않는다. fmap을 호출해도 값이 존재하지 않기 때문에 그대로 Nothing을 반환한다.

메이비와 리스트는 모두 어떤 값들을 담거나 비어 있는 컨테이너형 타입이다. 펑터는 타입생성자에서 컨테이너형 타입을 요구한다. 따라서 어떤 값을 담는 타입은 항상 펑터로 만드는 것을 고려해 볼 수 있다.

트리 펑터 만들기

이진 트리는 어떤 값을 담을 수 있는 컨테이너형 타입이다. 따라서 펑터로 만드는 것을 고려해 볼 수 있다.

트리의 요구사항은 다음과 같다.

트리는 비어 있거나 어떤 값과 두 개의 자식 트리를 가진다.
새로운 트리를 만들 수 있다.(treeOf)
트리를 화면에 출력할 수 있다.(toString)
트리의 모든 노드의 값을 변환 함수에 적용한 트리를 만들 수 있다.(fmap)

sealed class Tree<out A>: Functor<A> {
  abstract override fun toString(): String
  
  abstract override fun fmap(f: (A) -> B): Tree<B>
}

첫번째 요구사항대로 Tree는 비어있거나 어떤 값과 두 개의 자식 트리를 가져야 하므로 다음과 같이 비어있는 트리에 대한 값 생성자를 작성하자.

object Empty Tree: Tree<kotlin.Nothing>() {
  override fun toString(0: String = "E"
  
  override fun <B> fmap(f: (Nothing) -> B): Tree<B> = EmptyTree 
}

이제 어떤 값과 두 개의 자식 트리를 가진 Node 값 생성자를 구현하자.

data class Node,out A>(val value: A, val leftTree: Tree<A>, val rightTree: Tree<A>): Tree<A>() {
  override fun toString(0: String = "(N $value $leftTree $rightTree)"
  
  override fun <B> fmap(f: (A) -> B): Tree<B> = Node(f(value), leftTree.fmap(f), rightTree.fmap(f))
}

이더 펑터 만들기

메이비와 트리는 타입 생성자의 매개변수가 한개뿐이었다.
만약 타입 매개변수가 두개 이상인 타입을 펑터의 인스턴스로 만드려면 어떻게 해야 할까.

이더는 래프트, 라이트 타입만 허용하는 대수적 타입이다. 이더는 일반적으로 함수의 반환값으로 사용된다. 함수 호출이 성공하면 올바른 결과를 라이트에 담고 실패 이유에 대한 정보를 래프트로 표시한다.
따라서 래프트와 라이트가 포함하는 값의 타입은 다를 수 있다. 이더의 라이트의 값을 변경하고 변경된 값을 가진 이더를 얻을 수 있다.

이더는 메이비나 트리와 달리 타입 매개변수가 두 개다.
이더는 일반적으로 라이트의 값만 변경할 수 있다. 래프트의 값은 생성되는 시점에 고정된다.

sealed class Either<out L, out R>: Functor<R> {
  abstract override fun <R2> fmap(f: (R) -> R2): Either<L, R2>
}

래프트와 라이트 값 생성자를 구현해보자.

data class Left<out L>(val value: L): Either<L, Nothing>() {
  override fun <R2> fmap(f: (Nothing) -> R2): Either<L, R2> = this
}

data class Right<out R>(val value: R): Either<Nothing, R>() {
  override fun <R2> fmap(f: (R) -> R2): Either<Nothing, R2> = Right(f(value))
}

단항 함수 펑터 만들기

함수형 언어에서 함수는 일급 객체로 다루기 때문에 함수 펑터를 만들어보려고 한다.
Funtor 타입 클래스의 타입 생성자는 하나의 매개변수만 가진다. 하지만 함수의 타입은 함수의 매개변수가 여러 개인 경우 하나 이상의 타입 매개변수를 가질 수 있기 때문에 변경할 수 있는 타입 한 개를 제외하고 나머지는 고정해두어야 한다.

여기서는 매개변수가 한 개인 단항 함수에 대한 펑터를 만드는 것으로 제한한다.

data class UnaryFunction<in T, out R>(val g: (T) -> R) {
  override fun <R2> fmap(f: (R) -> R2): UnaryFunction<T, R2> {
    return UnaryFunction { x: T -> f(g(x)) }
  }
  
  fun invoke(input: T): R = g(input)
}

여러 가지 타입을 가질 필요가 없기 때문에 sealed class로 만들 필요가 없어 data class로 만들었다. 함수의 타입 매개변수는 입력 T와 출력 R이다. 함수의 입력은 고정하고 출력만 매핑하기 위해 펑터의 타입을 Funtor<R>로 선언했다.

fun main() {
  val f = { a: Int -> a + 1 }
  val g = { b: Int -> b * 2 }
  
  val fg = UnaryFunction(g).fmap(f)
  println(fg.invoke(5))
}

함수 g에 f를 적용하여 매핑한다는 것이 함성함수 원리랑 비슷한데, 이렇게 함수 합성을 이용하면 입력 매개변수가 여러 개인 함수도 만들 수 있다. UnaryFunction을 체이닝하면 결국 입력이 여러 개 인 함수와 동일하기 때문이다.
((T) -> R) -> R2 는 매개변수가 한개인 함수의 체이닝인 (T) -> ((R) ->R2)로 변경할 수 있다. 이는 커링과 동일한 원리로 이러한 원리를 사용해 값을 감싸고 있는 펑터(컨텍스트)를 변경할 수 있다.

fun main() {
  val g = { a: Int -> a * 2 }
  val k = { b: Int -> Just(b) }
  val kg = UnaryFunction(g).fmap(k)
  println(kg.invoke(5)) // "Just(10)"
}

UnaryFunction은 숫자를 받아서 Maybe를 반환했고 함수 k에 따라서 Tree나 Either를 반환할 수 있다. 이러한 함수를 일반적으로 승급(lifting) 함수라고 한다.

펑터의 법칙

펑터의 인스턴스가 되려면 두 가지 법칙을 만족해야 한다. 이것을 펑터의 법칙이라고 한다.

펑터 제 1법칙

fmap(identity()) === identity()

쉐도 코드로 써보자

fmap id  ==  id

fmap을 호출할 때 항등 함수 id를 입력으로 넣은 결과는 반드시 항등 함수를 호출한 결과와 동일해야 한다. 여기서 항등 함수는 { x -> x }와 같이 인풋에 대한 어떠한 가공 없이 그대로 반환하는 함수를 말한다.

The first functor law states that if we map the id function over a functor, the functor that we get back should be the same as the original functor.

원문

먼저 항등 함수는 다음과 같다.

fun <T> identity(x: T): T = x

Maybe, Either에 펑터 1법칙을 시험해보면 다음과 같다.

fun main() {
  println(Nothing.fmap { identity(it) } == identity(Nothing)) // true
  println(Just.fmap { identity(it) } == identity(it)) // true
}

각 펑터 인스턴스의 fmap 함수에 입력으로 identity를 넣어서 호출한 결과는, identity 함수에 펑터의 인스턴스를 넣어서 호출한 결과와 모두 동일하다.

펑터 제 2법칙

함수 f,g가 있을 때

fmap(f compose g) == fmap(f) compose fmap(g)

함수 f와 g를 먼저 함성하고 fmap 함수의 입력으로 넣어서 얻은 결과 값은 함수 f를 fmap에 넣은 함수와 g를 fmap에 넣은 함수를 합성한 결과와 같아야 한다.

infix fun <F, G, R> ((F) -> R).compose(g: (G) -> F): (G) -> R {
  return { gInput: G -> this(g(gInput)) }
}

fun main() {
  val f = { a: Int -> a + 1 }
  val g = { b: Int -> b * 2 }
  
  val nothingLeft = Nothing.fmap(f compose g)
  val nothingRight = Nothing.fmap(g).fmap(f)
  
  val justLeft = Just(5).fmap(f compose g)
  val jusetRight = Just(5).fmap(g).fmap(f)
}

마치며

오늘은 펑터에 대해 알아보았다. 다음 포스팅에서는 어플리케이티브 펑터에 대해 알아보겠다.

dante Yoon

성장을 향한 작은 몸부림의 흔적들

이전 포스트