백준 1644 소수의 연속합

Intro

Solution

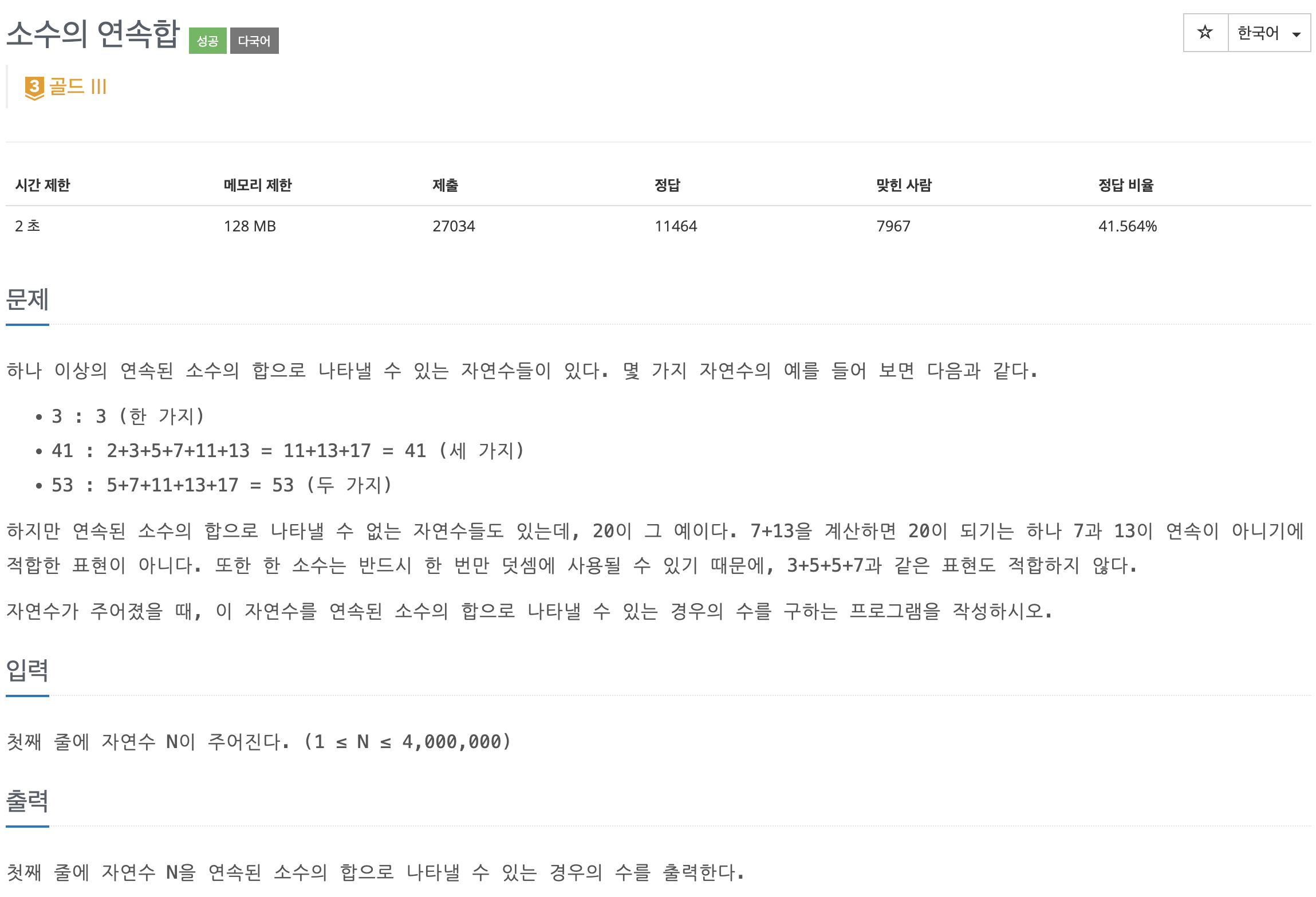
입력되는 수보다 작은 소수들을 합하여 입력된 수를 만들어야 하고, 해당 소수들은 연속된다.

1. 먼저 에라토스테네스의 체를 이용하여 입력 이하의 소수의 목록을 만든다.

2. 소수 목록의 누적 합 리스트를 만든다.

3. 투 포인터(l, r)를 이용해 포인터를 뒤로 옮겨가며 답을 구한다.
   3.1. 포인터 l부터 포인터 r까지의 소수의 합이 n과 동일할 때 정답으로 출력할 변수에 1을 더한다.
   3.2. 소수의 합이 n보다 작으면 오른쪽 포인터를 한 칸 이동한다.
   3.3. 소수의 합이 n보다 크거나 같으면 왼쪽 포인터를 한 칸 이동한다.

Code

def primes(n):
	if n < 2:
		return [0]
	is_prime = [True] * (n+1)
	for i in range(2, n+1):
		if is_prime[i]:
			for j in range(i+i, n+1, i):
				is_prime[j] = False
	return [k for k in range(2, n+1) if is_prime[k]]

def solve():
	n = int(input())

	prime = primes(n)
	csum = [0]
	[csum.append(csum[i] + prime[i]) for i in range(len(prime))]
	
	answer = 0
	l, r = 0, 1

	while r <= len(prime):
		num = csum[r] - csum[l]
		if num == n:
			answer += 1
			l += 1
		elif num < n:
			r += 1
		else:
			l += 1
	
	print(answer)


solve()