Python Cost & Gamma

Jayce_97·2023년 7월 7일

Python SVM

목록 보기

4/4

이번 시간에는 SVM에 사용되는 Cost와 Gamma에 대해서 배워보도록 하겠습니다.

Cost & Gamma

코스트와 감마는 SVM에서 사용되는 매개변수로써 데이터를 분류 하기 위해서 사용됩니다.
선형 SVM에서는 코스트의 값만 매개변수로 사용되는데, 현재 자주 사용되는 SVM은 *RBF커널 SVM이기 때문에 코스트와 감마가 함께 매개변수로 사용됩니다.

cost : 데이터 샘플들이 다른 클래스에 놓이는 것을 허용하는 정도
- 낮게 설정하면 이상치들이 있을 가능성을 크게 잡아 일반적인 결정 경계를 찾아내고, 높게 설정 하면 반대로 이상치의 존재 가능성을 작게 봐서 좀 더 세심하게 결정 경계를 찾아낸다.
- C가 낮으면 과소적합, 높으면 과적합이 일어난다.
gamma : 하나의 데이터 샘플이 영향력을 행사하는 거리를 결정
- 데이터가 클 수록 작은표준편차 즉, 영향력이 짧아진다.

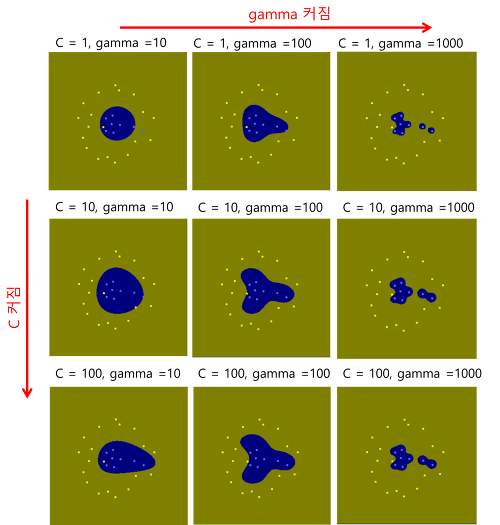
두 값이 커질수록 알고리즘의 복잡도는 증가합니다. 일반적으로 grid search를 이용하여 최적의 값을 찾을 수 있습니다.

SVM의 default 값은 rbf입니다.
RBF는 가우시안 방사 기저 함수(radial basis function)으로 불리며,
특정 샘플을 랜드마크로 지정해서 각 샘플이 랜드마크와 얼마나 유사한지를 구하는 유사도 함수를 대입합니다. 나온 결과값을 해당 샘플의 새로운 특성으로 추가하고, 이를 기준으로 결정 경계를 만드는 방식입니다.

C와 gamma 이해하기

input

import matplotlib.pyplot as plt 
import mglearn 
fig, axes=plt.subplots(3,3,figsize=(15,10))

for ax, C in zip(axes, [-1,1,3]):
    for a, gamma in zip(ax, [-1,0,1]):
        mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a)

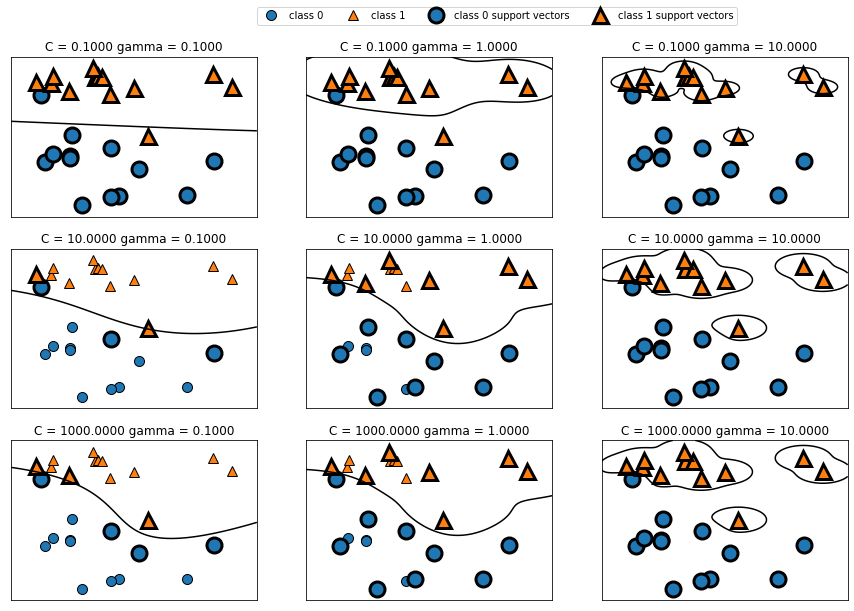
axes[0,0].legend(['class 0', 'class 1', 'class 0 support vectors', 'class 1 support vectors'], ncol=4, loc=(1, 1.2))

output

C와 gamma의 차이에 따라 분류의 방식이 달라지는 것을 확인할 수 있습니다.

데이터셋 불러오기

input

import matplotlib.pyplot as plt 
from sklearn.datasets._samples_generator import make_blobs 
X,y=make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.6)
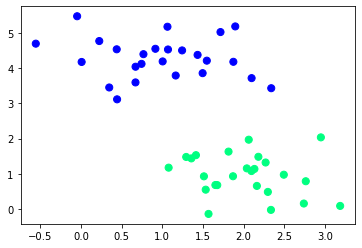
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='winter')

output

datasets 모듈을 이용하여 2가지 종류의 데이터를 불러옵니다.

데이터분류

input

import numpy as np 
xfit=np.linspace(-1, 3.5, 10)
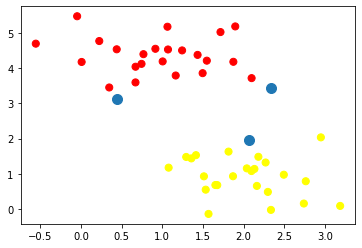
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
plt.plot([0.6],[2.1],'x',color='red',markersize=20)
for m,b in [(1,0.65),(0.5,1.6),(-0.2,2.9)]:
    plt.plot(xfit, m*xfit+b)
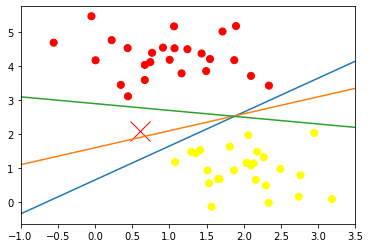
plt.xlim(-1,3.5)

output

새로운 데이터 값이 들어갔을 때를 가정하여 직접 분류선을 그어보았습니다.

모델 학습

input

from sklearn.svm import SVC 
model=SVC(kernel='linear')
model.fit(X,y)

output

벡터값 표출

input

plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
plt.scatter(model.support_vectors_[:,0], model.support_vectors_[:,1],s=100)

output

벡터값 샘플이 어느 위치에 생성되는지 확인합니다.

input

def plot_svc(model, ax=None):
    if ax==None:
        ax=plt.gca() #새로운 그래픽 객체 생성
    xlim=ax.get_xlim()
    ylim=ax.get_ylim()
    x=np.linspace(xlim[0], xlim[1], 30)
    y=np.linspace(ylim[0], ylim[1], 30)
    Y, X=np.meshgrid(y,x) #정방행렬
    xy=np.vstack([X.ravel(), Y.ravel()]).T  #행렬 전치
    P=model.decision_function(xy).reshape(X.shape) #판별함수에 입력 
    #등고선 그래프
    ax.contour(X,Y,P,levels=[-1,0,1],linestyles=['--','-','--'])
    ax.scatter(model.support_vectors_[:,0], model.support_vectors_[:,1],s=200)
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)
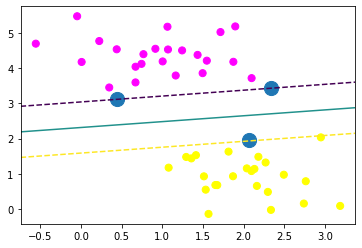
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='spring')
plot_svc(model)

output

최적의 초평면과 최대마진을 시각화하여 확인해 줍니다.

Cost 적용

input

X,y=make_blobs(n_samples=100,centers=2,random_state=0,cluster_std=0.8)
fig,ax=plt.subplots(1,3,figsize=(24,6))
for axi,cost in zip(ax,[100,1,0.1]):
    model=SVC(kernel='linear',C=cost).fit(X,y)
    axi.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
    plot_svc(model,axi)
    axi.scatter(model.support_vectors_[:,0], model.support_vectors_[:,1],s=50,lw=4)
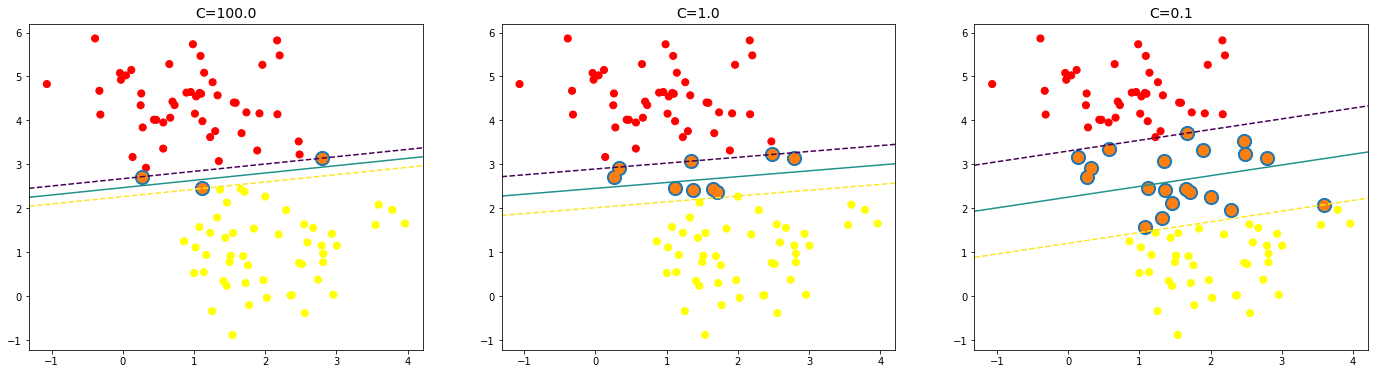
    axi.set_title('C={:.1f}'.format(cost), size=14)

output

cost에 따라 최적의 초평면과 최대마진의 값이 달라지는 것을 확인 할 수 있습니다.

gamma 적용

input

X,y=make_blobs(n_samples=100,centers=2,random_state=0,cluster_std=0.8)
fig,ax=plt.subplots(1,3,figsize=(24,6))
for axi,g in zip(ax,[10,1,0.1]):
    model=SVC(kernel='rbf',gamma=g).fit(X,y)
    axi.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
    plot_svc(model,axi)
    axi.scatter(model.support_vectors_[:,0], model.support_vectors_[:,1],s=50,lw=4)
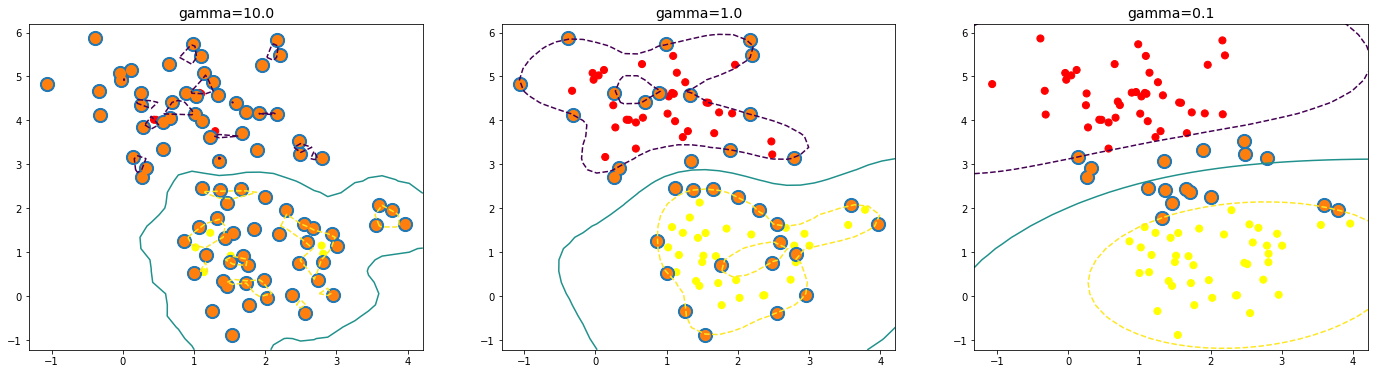
    axi.set_title('gamma={:.1f}'.format(g), size=14)