R-squared 와 P-value

회귀분석

• R-Squared(결정계수)

  • 회귀모델에서 독립변수(일반적으로: X) 종속변수(y) 얼마나 설명하는지 알려주는 지표
  • 종속변수가 추가 되는 것만으로도 점수가 올라가기 때문에 유의
  • $R^2 = \frac{SSE}{SST} = 1-\frac{SSR}{SST}$
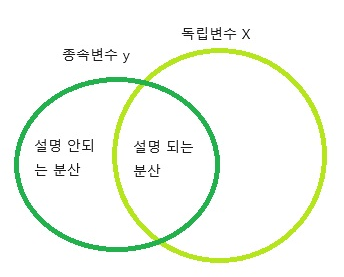
  • SST(Total Sum of Squares), 총제곱합
    • $SST = \sum_{i=1}^{n}(y_i - \bar y)^2$
    • (관측값 - 평균) 제곱
    • SST는 관측값에서 관측값의 평균(혹은 예측치의 평균)을 뺀 결과의 총합
  • SSE(Explained Sum of Squares), 회귀제곱 합
    • $SSE = \sum_{i=1}^{n}(\hat y_i - \bar y)^2$
    • (예측값 - 평균)의 제곱합, 설명된 분산
    • SSE는 추정값에서 관측값의 평균(혹은 예측치의 평균)을 뺀 결과의 총합
  • SSR(Residual Sum of Squares), 잔차 제곱합
  • $SST = \sum_{i=1}^{n}(y_i - \hat y)^2$
    • (관측값 - 예측값)의 제곱합 → 설명 되지 않은 분산
    • SSR은 관측값에서 예측값을 뺀 값(잔차(Residual)의 총합
  • 해당 내용들은 계산해주는 Python 코드가 있습니다(ex summary)

• 이 부분은 한 블로그에서 개인적인 해석을 가져왔습니다

  • T = R + E라는 공식을 인용
    • $전체차이(T) = 엉망회귀~회귀(R) or 개선된 차이(R) + 회귀~관측(E) or 여전히 남은 차이(E)$
    • $R^2 = \frac{개선된 차이}{전체오류} = \frac RT$

• Adjusted R-Squared(조정된 결정계수)

  • R-Squared의 단점인 종속변수가 추가 되는 것만으로도 점수가 올라가는 것을 방지하기 위해 나온 방법
  • 독립변수가 증가 할때 분자를 감소 시켜주는 방법으로 일방적인 증가를 방지
  • n = 샘플 수(데이터 개수), k = 독립변수(일반적으로 X)일 때
  • $Adjusted R^2 = 1-\frac {SSR/(n-k-1)}{SST/(n-1)}$

• P-Value(Probability-value)

  • 어떤 사건이 우연히 발생할 확률
  • 즉 값이 낮을 수록 우연히 생성된 값이 아니므로 유의미한 데이터라고 생각할 수 있다.
  • 해당 값은 귀무가설에 의해 선정되는데 해당 내용은 나중에 다루도록 하겠습니다.(귀무가설,대립가설의 중요도를 판단 후)
  • 일반적으로 P-value는 0.05 이하의 값을 가졌을 때 유의미한 변수라고 산정합니다

• 사용예시

  import statsmodels.api as sm 
  model=sm.Logit(y_train.astype(float),X_train.astype(float))
  result=model.fit()
  print(result.summary2())

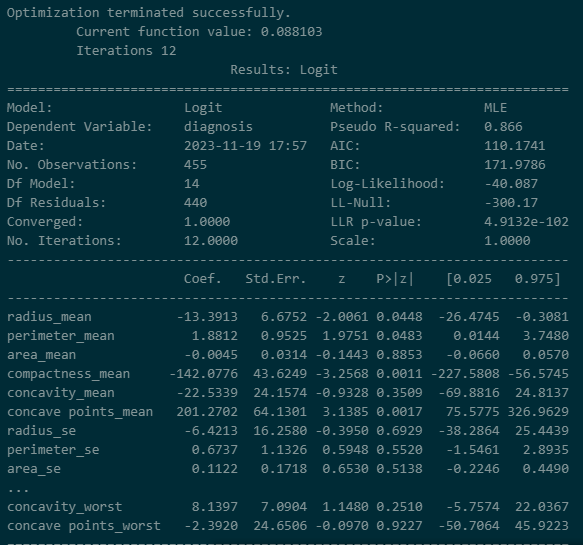
• 해당 내용은 Breast데이터 셋에서 corr(상관관계)가 높은 변수들만 뽑아서 확인한 값입니다.
• 해당 모델은 86.6%의 설명력을 가지며 유의미한 변수는 radius_mean, perimeter_mean, compactness_mean, concave points_mean등 이라고 판단하였습니다. 이것을 기준으로 잡고 p-value 값이 높은 변수를 삭제 한다던가 하는 데이터 삭제 이유를 생각 할 수 있습니다. 또한 coef(기울기)를 통해 반경의 작을 수록 1에 가깝다 등을 알 수 있습니다.

R-squared : 모델의 설명력을 갖는가

P-value : 모형이 통계적으로 유의미 한가, 회귀계수가 유의한가를 확인 가능합니다

총정리

R-Squared는 모델에 사용된 독립변수의 논리성/이론적 근거이며 P-value는 해당 변수가 유의미한 변수인가를 확인 할 수 있습니다.