BombLab - Phase 4

beans_I·2024년 2월 23일

bomblab 밤랩 시스템프로그래밍

[23-2] 시스템 프로그래밍

목록 보기

4/6

Phase 4

Phase 4는 재귀 함수 func4의 동작을 파악하는 것이 핵심이다. 이전 단계들보다 복잡성이 증가하지만, 전체 구조를 먼저 파악하면 어렵지 않게 해결할 수 있다.

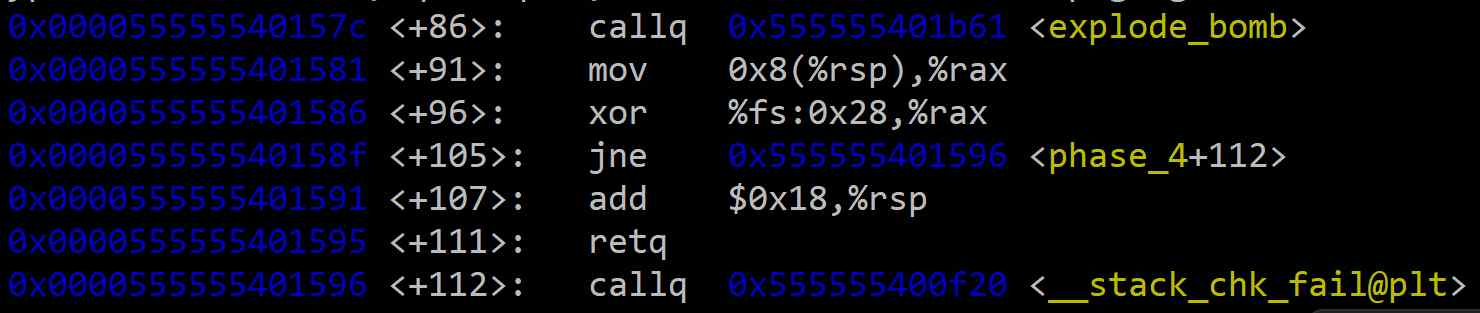
1. 시작 부분

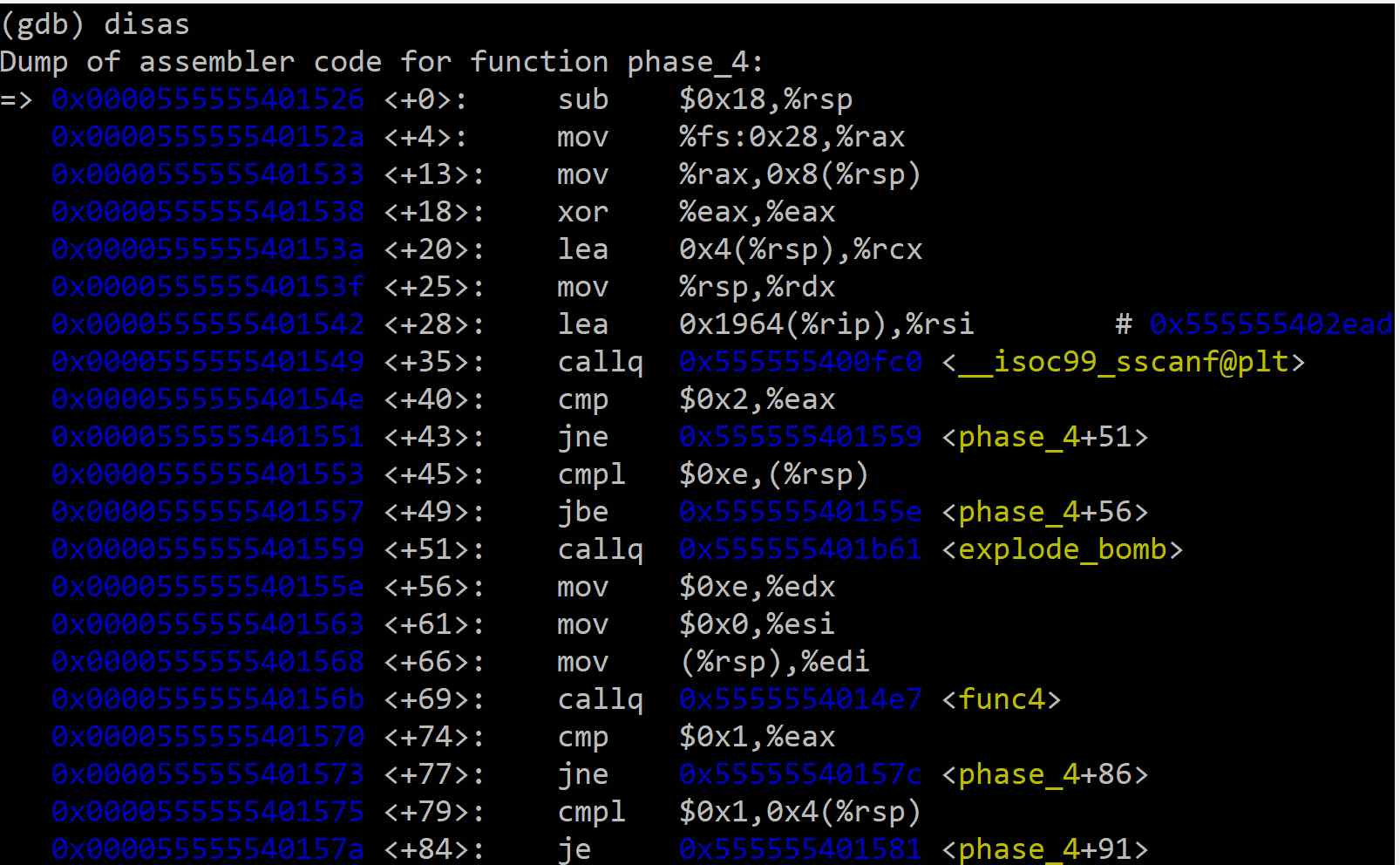
phase_4 함수의 시작 부분을 분석하면 다음과 같은 초기 조건을 알 수 있다.

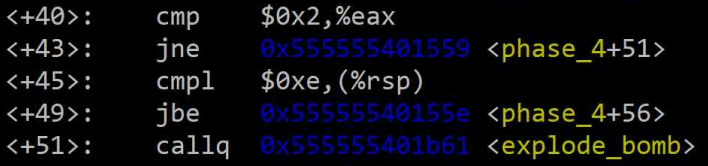
~ <+35> : 앞선 Phase 3처럼scanf의 포맷 문자열을 확인해보면 %d %d로, 2개의 정수를 입력받는것을 알 수 있다.
<+40>, <+43>, <+51> : 만약 2개가 아니면 폭탄이 터진다.
<+45>: 첫 번째로 입력한 정수는 0xe(15)와 비교되며, jbe (Jump if Below or Equal) 조건을 통해 0에서 15 사이의 값이어야 함을 알 수 있다.

<+56> 지점부터의 코드는 func4 함수에 전달될 인자(argument)를 설정하는 과정이다. x86-64 리눅스 호출 규약에 따라, 함수의 첫 세 인자는 %edi, %esi, %edx 레지스터를 통해 전달된다.

첫 번째 인자 (%edi): 사용자가 입력한 첫 번째 정수 값
두 번째 인자 (%esi): 상수 0
세 번째 인자 (%edx): 상수 15

결과적으로 호출되는 함수는 func4(첫 번째 입력값, 0, 15)와 같다. 이 분석을 기점으로, 문제를 해결하기 위한 두 가지 다른 접근 방법을 사용할 수 있다.

2-1. 브루트 포스를 이용한 방식

이 방식은 func4을 분석하지 않고, 함수가 반환된 후의 최종 조건들을 먼저 확인하는 효율적인 접근법이다. func4는 사진과 같이 재귀 함수이기 때문에 해석하는데 오래 걸리기 때문이다.

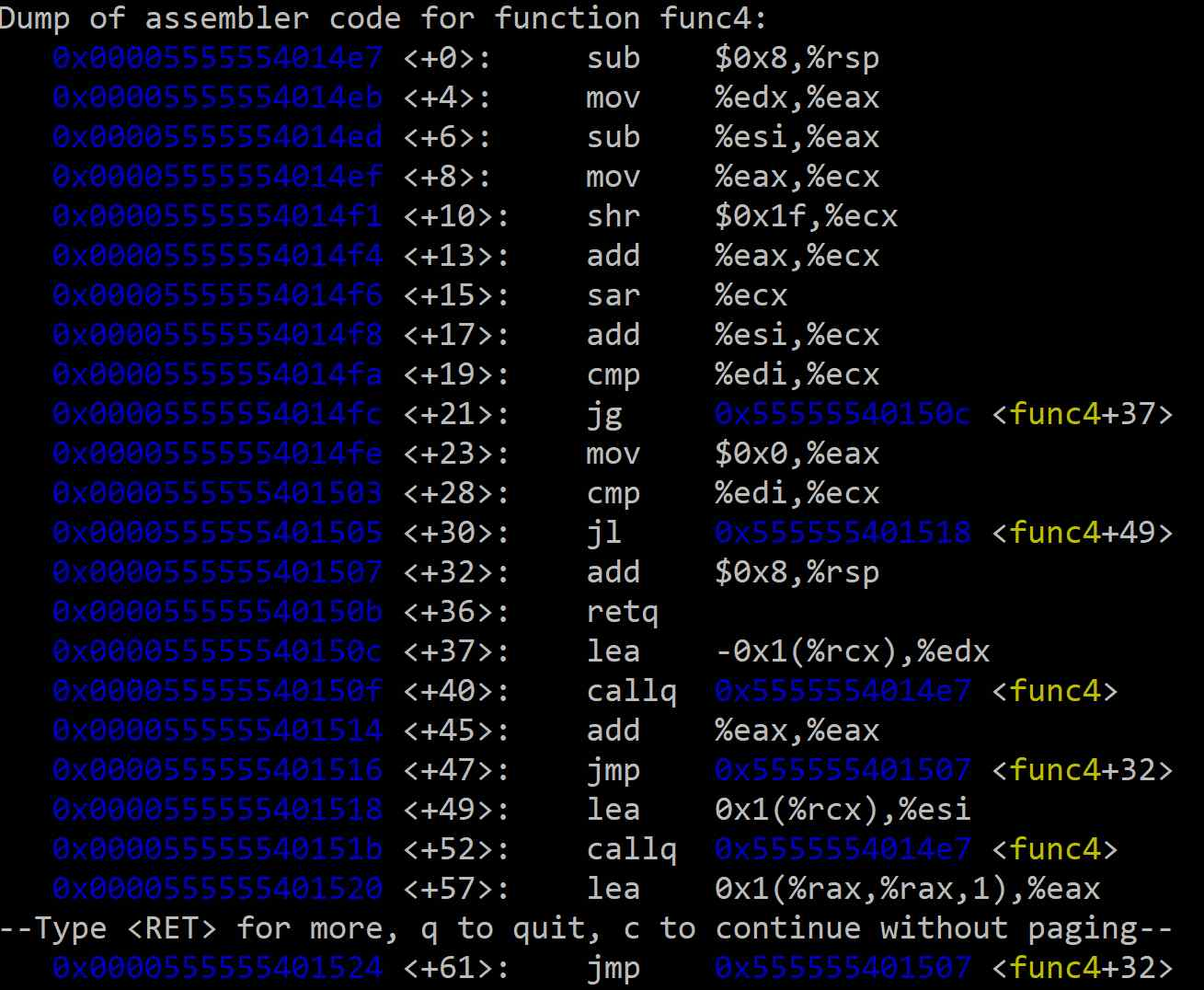
그리고 폭탄이 터지는 것은 GDB에서 explode_bomb에 중단점을 설정한 상태로 두면은 방지할 수 있기에 속도면에서 일반적인 풀이보다 빠르다.

그렇다면Phase 4에서 <func4>가 끝나는 <+74> 부터 보도록 하자.

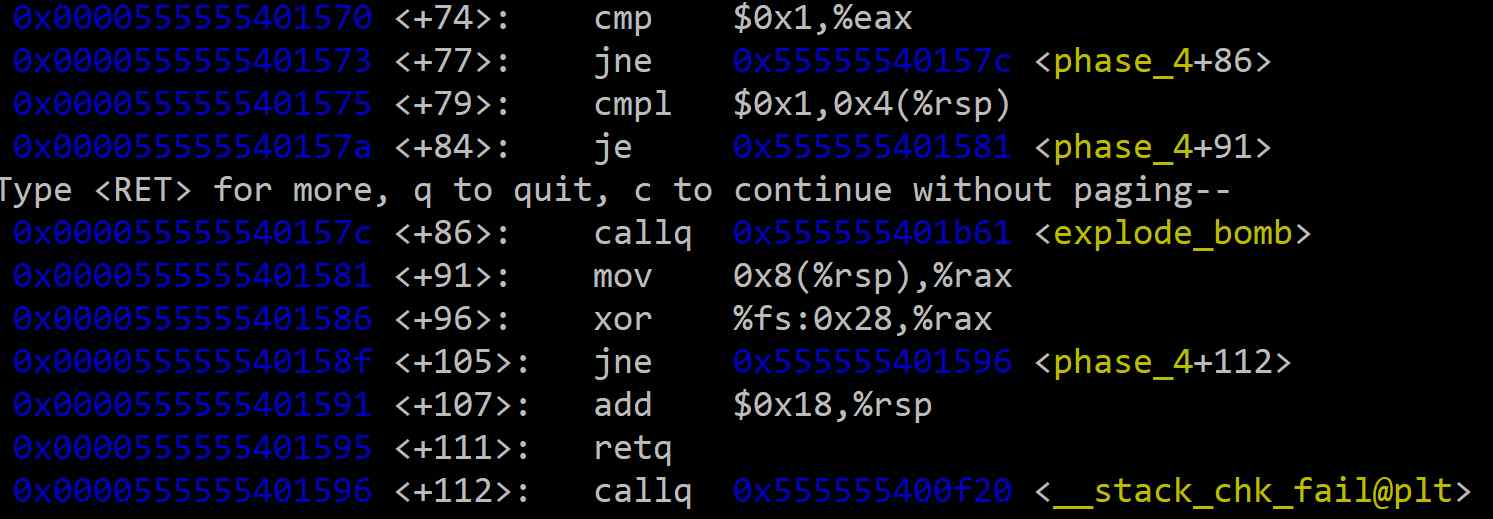
<+74>, <+77>: func4의 반환 값(%eax)이 반드시 1이어야 한다.
<+79>, <+84>: 사용자가 입력한 두 번째 정수가 반드시 1이어야 한다.

여기서 두 번째 입력값은 1로 고정됨을 알 수 있다. 첫 번째 입력값은 앞서 확인했듯이 0에서 15 사이의 정수이므로, 가능한 정답의 조합은 총 16가지(0 1부터 15 1까지)로 좁혀진다.

따라서 브루트 포스 방법을 사용하면, func4의 복잡한 로직을 이해하지 않고도 빠르고 간단하게 Phase 4를 해결할 수 있다.

2-2. func4 재귀 함수 분석

phase_4에서는 func4를 호출하기 전에 다음과 같이 세 개의 인자를 설정한다.

%edi: 사용자가 입력한 첫 번째 정수 (user_input)
%esi: 0 (탐색 범위의 시작, low)
%edx: 15 (탐색 범위의 끝, high)

따라서 최초 함수 호출은 func4(user_input, 0, 15)와 같다.

func4을 전체적으로 살펴보면은 이진 탐색과 유사한 로직을 가진 재귀 함수이다. 주요 로직은 다음과 같다.

2-2-1. 중간값 계산 (`<+4>` ~ `<+17>`):

<+4> ~ <+6> : high - low 계산
```
<+4>: mov    %edx,%eax  ; eax = high
<+6>: sub    %esi,%eax  ; eax = high - low
```
%eax 레지스터에 high - low의 결과가 저장된다. (low + high) / 2 형태로 계산할 경우 low + high 과정에서 정수 오버플로우가 발생할 수 있지만, low + (high - low) / 2 와 같이 high - low를 먼저 계산하면 이 문제를 원천적으로 방지할 수 있다.
<+8> ~ <+13>: 나눗셈을 위한 부호 보정
```
<+ 8>: mov    %eax,%ecx      ; ecx = high - low
<+10>: shr    $0x1f,%ecx     ; ecx = (high - low)의 최상위 비트(부호 비트)
<+13>: add    %eax,%ecx      ; ecx = (high - low) + (부호 비트)
```
- <+10> shr $0x1f, %ecx : 32비트 정수인 %ecx를 부호 없이 오른쪽으로 31비트 이동시켜 최상위 부호 비트(MSB)만 추출한다. high - low가 음수이면 %ecx는 1, 아니면 0이 된다.
- <+13> add %eax, %ecx : 원본 값에 부호 비트 값을 더한다.
  
  이 과정을 종합하면, 다음과 같다.
1. high - low가 음수일 경우: (high - low) + 1
2. high - low가 양수이거나 0일 경우: (high - low) + 0
  
  이 보정이 필요한 이유는 C언어의 나눗셈(0을 향한 버림)과 sar 명령어의 동작(음의 무한대를 향한 버림) 방식이 음수에서 다르기 때문이다. 예를 들어, C에서 -15 / 2는 -7이지만, 보정 없이 -15에 sar를 적용하면 -8이 된다. 위 코드는 음수일 때만 1을 더해줌으로써 sar의 결과가 C언어의 나눗셈 결과와 일치하도록 보정하는 역할을 한다.
<+15>: 2로 나누기
```
<+15>: sar    %ecx         ; ecx = ecx / 2 (산술 시프트)
```
sar (산술 우측 시프트) 명령어는 레지스터 값을 2로 나누는 효과를 가진다. 부호를 유지하며 나누므로, 앞선 보정 작업과 함께 올바른 (high - low) / 2 계산을 완료한다.
<+17>: low 더하기
```
<+17>: add    %esi,%ecx      ; ecx = ecx + low
```
마지막으로, 계산된 (high - low) / 2 값에 low(%esi)를 더하여 최종 중간값 mid = low + (high - low) / 2 를 %ecx에 저장하고 계산을 마친다.

2-2-2. `mid`와 `input` 비교 (`<+19>` ~ `<+30>`):

계산된 중간값 mid와 사용자 입력 user_input을 비교하여 세 가지 경우로 분기한다.

mid > input의 경우 (<+19> ~ <+21>, <+37> ~ <+47>)
```
<+19>: cmp    %edi,%ecx      ; mid와 input을 비교
<+21>: jg     <func4+37>     ; mid > input 이면 점프
...
<+37>: lea    -0x1(%rcx),%edx  ; edx = mid - 1 (새로운 high)
<+40>: callq  <func4>        ; func4(input, low, mid - 1) 재귀 호출
<+45>: add    %eax,%eax      ; eax = eax * 2
<+47>: jmp    <func4+32>     ; 함수 종료 지점으로 점프
```
- <+19> ~ <+21>: mid(%ecx)가 input(%edi)보다 크면(jg: Jump if Greater) <+37>로 분기한다.
- <+37>: 새로운 탐색 범위의 끝(high)을 mid - 1로 설정하여 %edx에 저장합니다.
- <+40>: func4(input, low, mid - 1)를 재귀 호출한다. low(%esi)와 input(%edi)은 그대로 유지된다.
- <+45>: 재귀 호출이 끝난 후 반환된 값(%eax)에 add %eax, %eax를 수행하여 결과를 2배로 만들어준다.
정리하면 탐색 범위를 상위 절반으로 좁힌 다음, func4(user_input, low, mid - 1)를 재귀 호출한다. 재귀 호출에서 반환된 값에 2를 곱하여 리턴한다.
mid < input의 경우 (<+28> ~ <+30>, <+49> ~ <+61>)
```
<+23>: mov    $0x0,%eax      ; eax = 0. 지금 케이스에서는 딱히 의미없음
<+28>: cmp    %edi,%ecx      ; mid와 input을 비교
<+30>: jl     <func4+49>     ; mid < input 이면 점프
...
<+49>: lea    0x1(%rcx),%esi   ; esi = mid + 1 (새로운 low)
<+52>: callq  <func4>        ; func4(input, mid + 1, high) 재귀 호출
<+57>: lea    0x1(%rax,%rax,1),%eax ; eax = eax * 2 + 1
<+61>: jmp    <func4+32>     ; 함수 종료 지점으로 점프
```
- <+28> ~ <+30>: mid(%ecx)가 input(%edi)보다 작으면(jl: Jump if Less) <+49>로 분기한다.
- <+49>: 새로운 탐색 범위의 시작(low)을 mid + 1로 설정하여 %esi에 저장한다.
- <+52>: func4(input, mid + 1, high)를 재귀 호출한다. high(%edx)와 input(%edi)은 그대로 유지된다.
- <+57>: 재귀 호출에서 반환된 값(%eax)에 lea 0x1(%rax,%rax,1),%eax를 수행합니다. 이는 %rax + %rax*1 + 1 즉, 결과를 2배로 만들고 1을 더하는 연산이다.
정리하면 탐색 범위를 하위 절반으로 좁혀 func4(user_input, mid + 1, high)를 재귀 호출한다. 재귀 호출에서 반환된 값에 2를 곱한 뒤, 1을 더하여 리턴한다.
mid == input의 경우 (<+23>, <+36>)
```
<+23>: mov    $0x0,%eax       ; eax = 0
...   (점프하지 않고 계속 진행)
<+36>: retq                  ; 함수 종료 및 값 리턴 
```
- <+23>: mid와 input이 같으면, 반환 값을 저장하는 %eax에 0을 넣는다.
- <+36>: retq 명령어를 통해 함수를 종료하고 %eax에 저장된 값, 즉 0을 반환한다.
이 케이스는 탐색에 성공하여 재귀를 탈출하는 베이스 케이스로, 0을 리턴하고 재귀를 종료한다.

2-2-3. 파이썬으로 해당 코드 구현 및 답 확인

이를 파이썬 코드로 정리하면 다음과 같다.

#1. 단순 어셈블리 코드 옮기기
def func4_assembly(edi: int, esi: int, edx: int) -> int:
    eax = edx                      # <+4>
    eax -= esi                     # <+6>
    ecx = eax                      # <+8>
    ecx = (ecx >> 31) & (0x7FFFFFFF >> 31) # <+10>, 논리 시프트
    ecx += eax                     # <+13>
    ecx = ecx >> 1                 # <+15>
    ecx += esi                     # <+17>
    if ecx > edi:                  # <+19>/<+21> -> goto <+37>
        edx = ecx - 1              # <+37>
        return 2 * func4_assembly(edi, esi, edx) # <+40> ~
    
    eax = 0                        # <+23>
    if ecx < edi:                  # <+28>/<+30> -> goto <+49>
        esi = ecx + 1              # <+49>, rcx - 64bit, ecx - 32bit
        return 2 * func4_assembly(edi, esi, edx) + 1 # <+52> ~
    
    return eax                     # <+36>

edx: int = 15
esi: int = 0
edi: int

for edi in range(0, 16):
    result = func4_assembly(edi, esi, edx)
    print(f"입력한 값이 {edi:2}일 때: func4 반환값 = {result}")

#2. 실제 작성되었을 코드로 옮기기
def func4(edi, esi, edx):
    # edi: 사용자 입력값 (user_input)
    # esi: 탐색 범위 시작 (low)
    # edx: 탐색 범위 끝 (high)

    if esi > edx:
        return -1

    # 중간값 계산
    mid = esi + (edx - esi) // 2

    if mid == edi:
        return 0
    elif mid > edi:
        return 2 * func4(edi, esi, mid - 1)
    else: # mid < edi
        return 2 * func4(edi, mid + 1, edx) + 1

# 0부터 15까지 모든 입력에 대해 func4의 반환값 확인
for i in range(16):
    result = func4(i, 0, 15)
    print(f"입력한 값이 {i:2d}일 때: func4 반환값 = {result}")

그리고 해당 코드를 실행하면은 다음과 같다.

입력한 값이  0일 때: func4 반환값 = 0
입력한 값이  1일 때: func4 반환값 = 0
입력한 값이  2일 때: func4 반환값 = 4
입력한 값이  3일 때: func4 반환값 = 0
입력한 값이  4일 때: func4 반환값 = 2
입력한 값이  5일 때: func4 반환값 = 2
입력한 값이  6일 때: func4 반환값 = 6
입력한 값이  7일 때: func4 반환값 = 0
입력한 값이  8일 때: func4 반환값 = 1
입력한 값이  9일 때: func4 반환값 = 1
입력한 값이 10일 때: func4 반환값 = 5
입력한 값이 11일 때: func4 반환값 = 1
입력한 값이 12일 때: func4 반환값 = 3
입력한 값이 13일 때: func4 반환값 = 3
입력한 값이 14일 때: func4 반환값 = 7
입력한 값이 15일 때: func4 반환값 = 15

[Execution complete with exit code 0]