DFS (Depth-First Search)

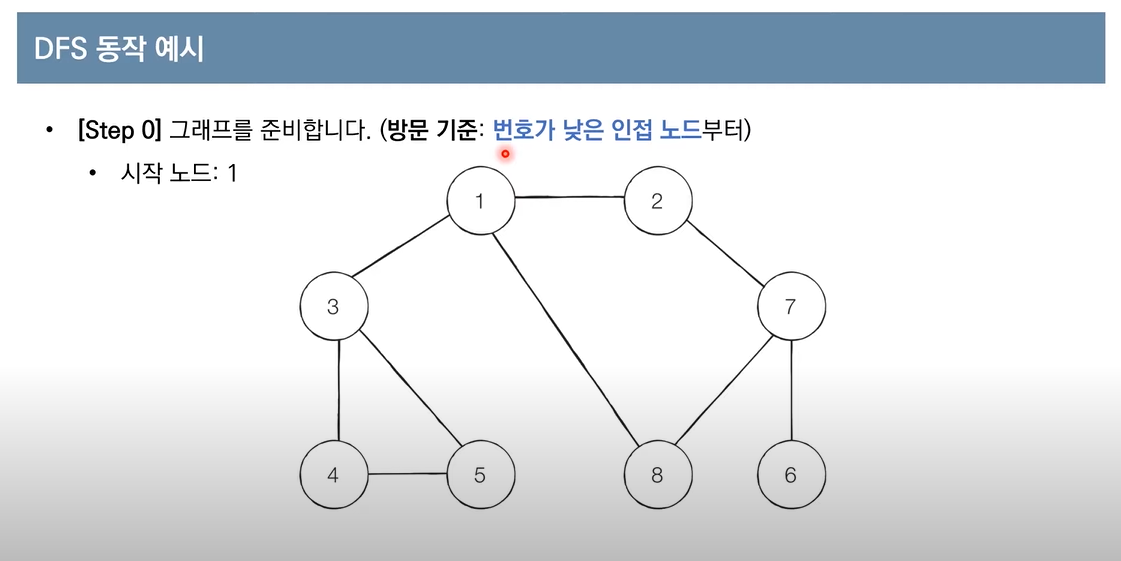
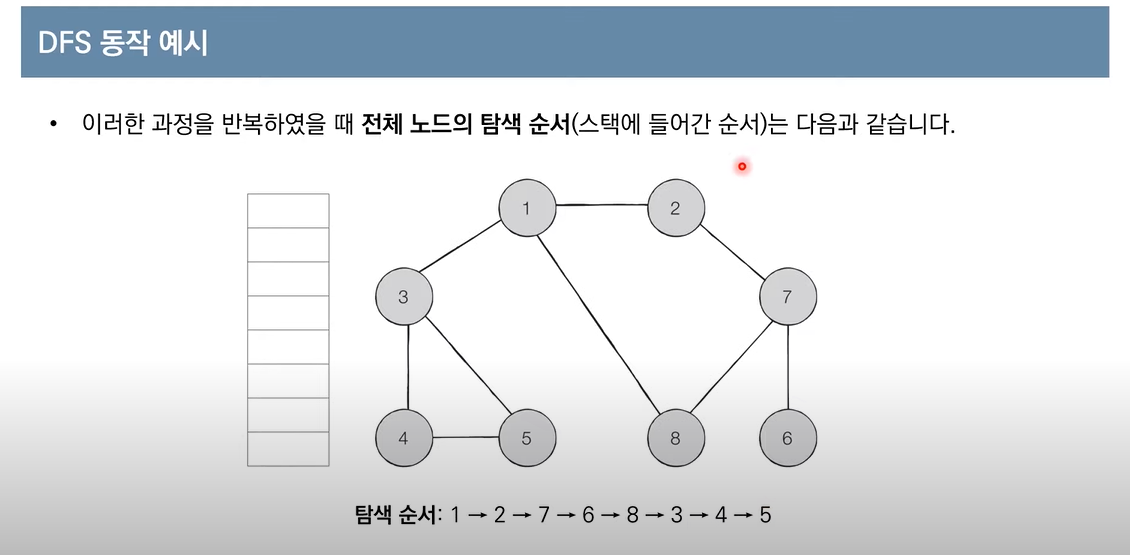
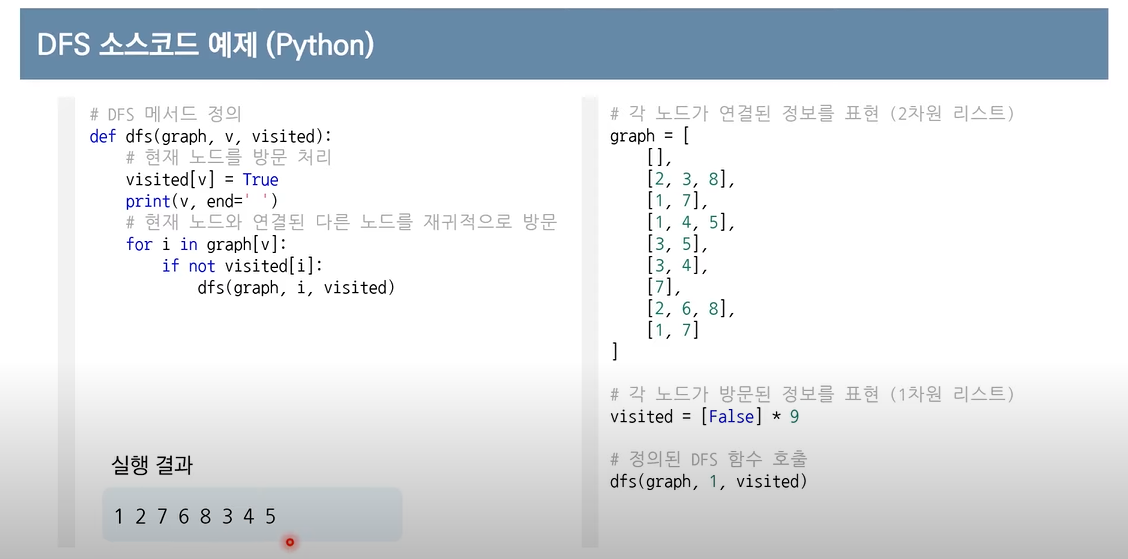
DFS -> Stack 이용
재귀 -> Stack
DFS -> 재귀 이용하면 좋음

위 코드에서 재귀가 리턴 되면서(Stack) 최대 깊이인 6까지 갔다가 1로 다시 돌아오고 다시 탐색을 시작한다.

문제 설명

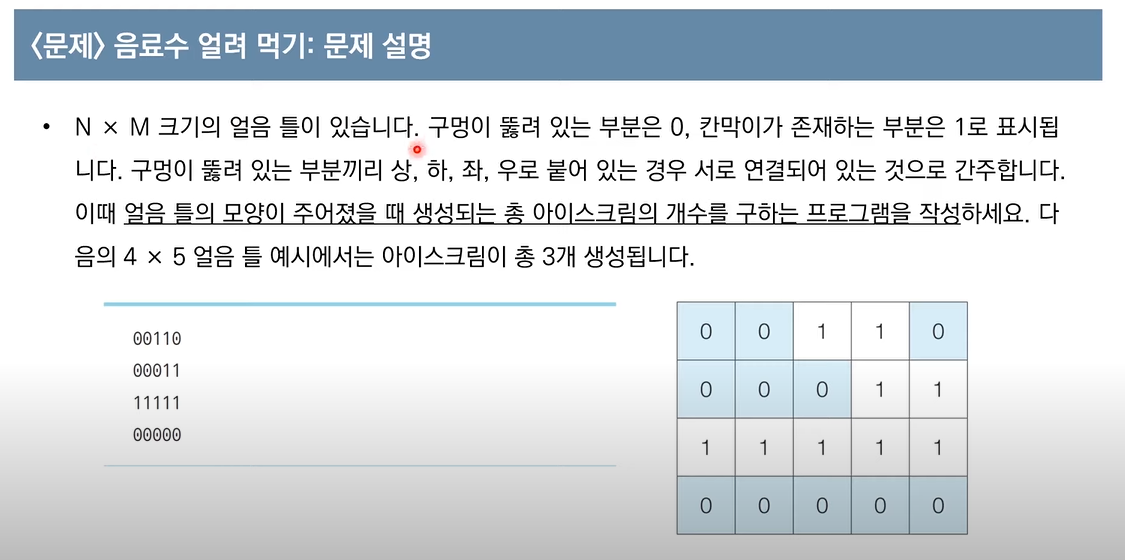
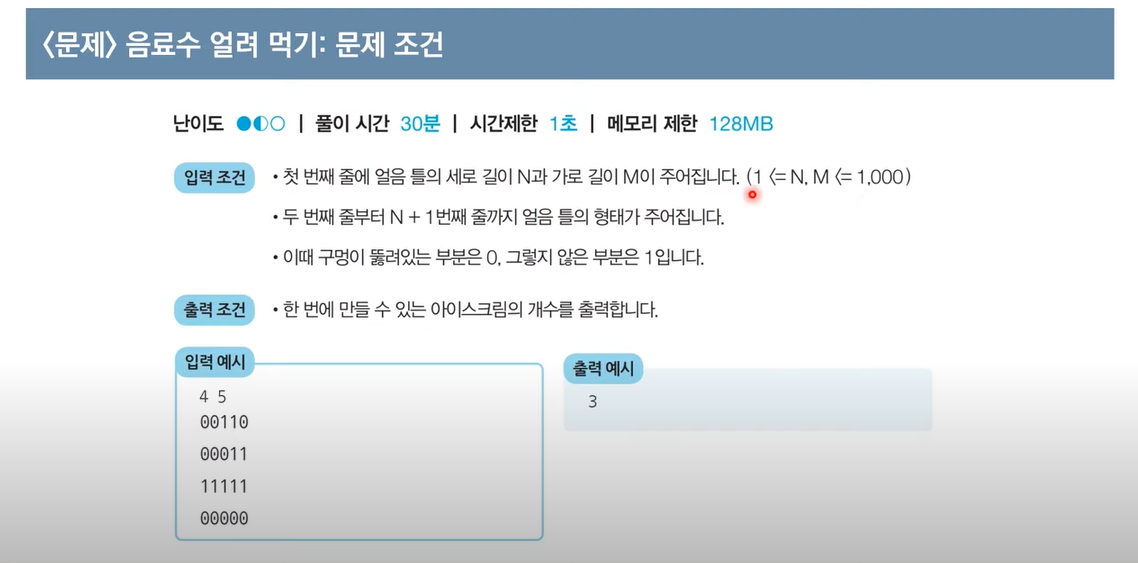
문제 검토

완전 탐색을 하기 충분한 입력값의 범위를 가진 문제이다.
허나 0 부분만을 탐색할 때 순서대로 탐색하기엔 복잡하고 어려워 보인다.

n*m 리스트를 그래프로 변경할 수 있다는 걸 알고 깊이 우선 탐색(DFS)를 사용해서 1을 방문 흔적으로 잡고 0이 있는 곳만을 방문해서 해답을 구할 수 있다.

풀이

def DFS(x,y):
#범위를 벗어나는 노드가 있다면 그 즉시 return 한다.
    if x<0 or y<0 or x>=n or y>=m:
        return
#만약 현재 노드를 방문하지 않았다면  
    if graph[x][y]==0:        
#방문처리 및 상하좌우 노드 DFS탐색
        graph[x][y] = 1
        DFS(x-1,y)
        DFS(x,y-1)
        DFS(x+1,y)
        DFS(x,y+1)
#이렇게 인접한 노드를 모두 방문처리하고 True를 반환한다.     
        return True
#현재 노드가 방문처리가 되어 있다면 계속 진행할 수 있도록 False를 반환해준다.      
    return False
        

n,m = map(int,input().split())

graph = [list(map(int,input())) for x in range(n)]
result=0

#모든 노드를 DFS한다.
for x in range(n):
    for y in range(m):
        if DFS(x,y):
            result+=1
            
print(result)

모든 노드를 DFS하지만 인접해있는 노드 중 한 노드만 DFS가 들어간다면 스택구조의 재귀로 인해서 그 노드의 인접하고 인접한 노드들은 전부 방문처리 되기 때문에 모든 노드에서 재귀가 되지는 않는다.

걸린 시간

24분 08초

총평

2차원 리스트를 그래프로 바꿀 수 있다는 점에 주목하고 깊이 우선 탐색을 통하여 탐색하기 어려운 구조 또한 효과적으로 탐색할 수 있음을 인지하자.