
목차
1. DFS
2. 그림으로 이해
3. 코드
4. 느낀점
DFS
이번에는 DFS에 대해서 알아보자.
DFS는 그래프 완전 탐색 기법중 하나이다.
기본적으로 그래프에서 시작노드부터 탐색할 부분을 정하여 먼저 끝까지 탐색을 한다.
DFS알고리즘 이용시 recursion error가 자주 뜨기도 한다.
이런 경우 보통 BFS를 이용하거나 메모이제이션 기법을 적용하여 DP로 풀어서 해결하게된다.
DFS는 재귀함수를 이용하여 구현하게 되므로 스택의 원리를 이해하고 있어야한다..
그림으로 이해
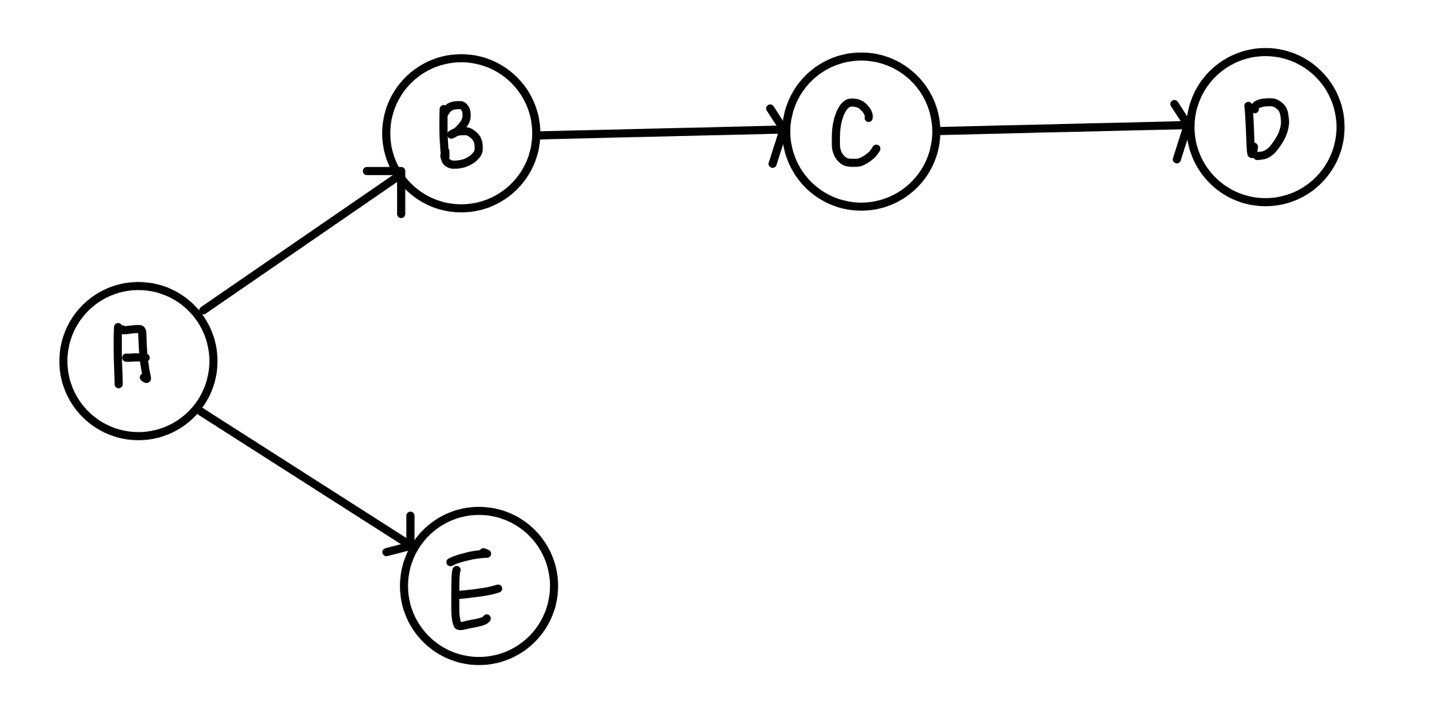
아래와 같은 그래프가 있다고 가정하자.
A 노드를 시작 노드로 하여 DFS 탐색을 하면 자신이 어떤 노드부터 방문할 지 정하게 된다.
여기서는 만약 두개의 노드와 연결되어있다면 위쪽부터 탐색하도록 하겠다.
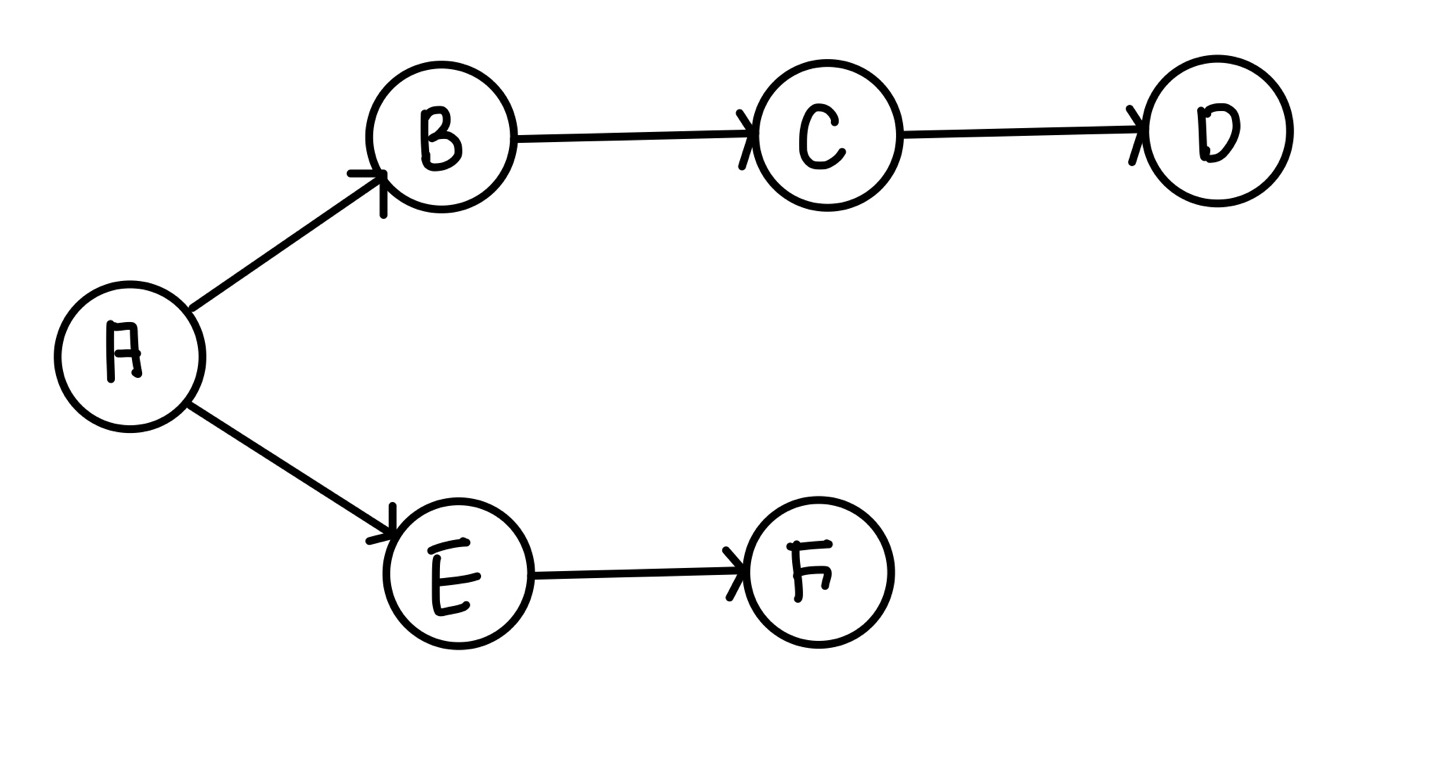
처음 A노드에서 갈 수 있는 길은 B로 갈 수 있는 경로와 E로 갈 수 있는 경로로 나뉜다.

우리는 조건에서 위쪽을 먼저 가기로 했으므로 B를 먼저 탐색하게 된다.
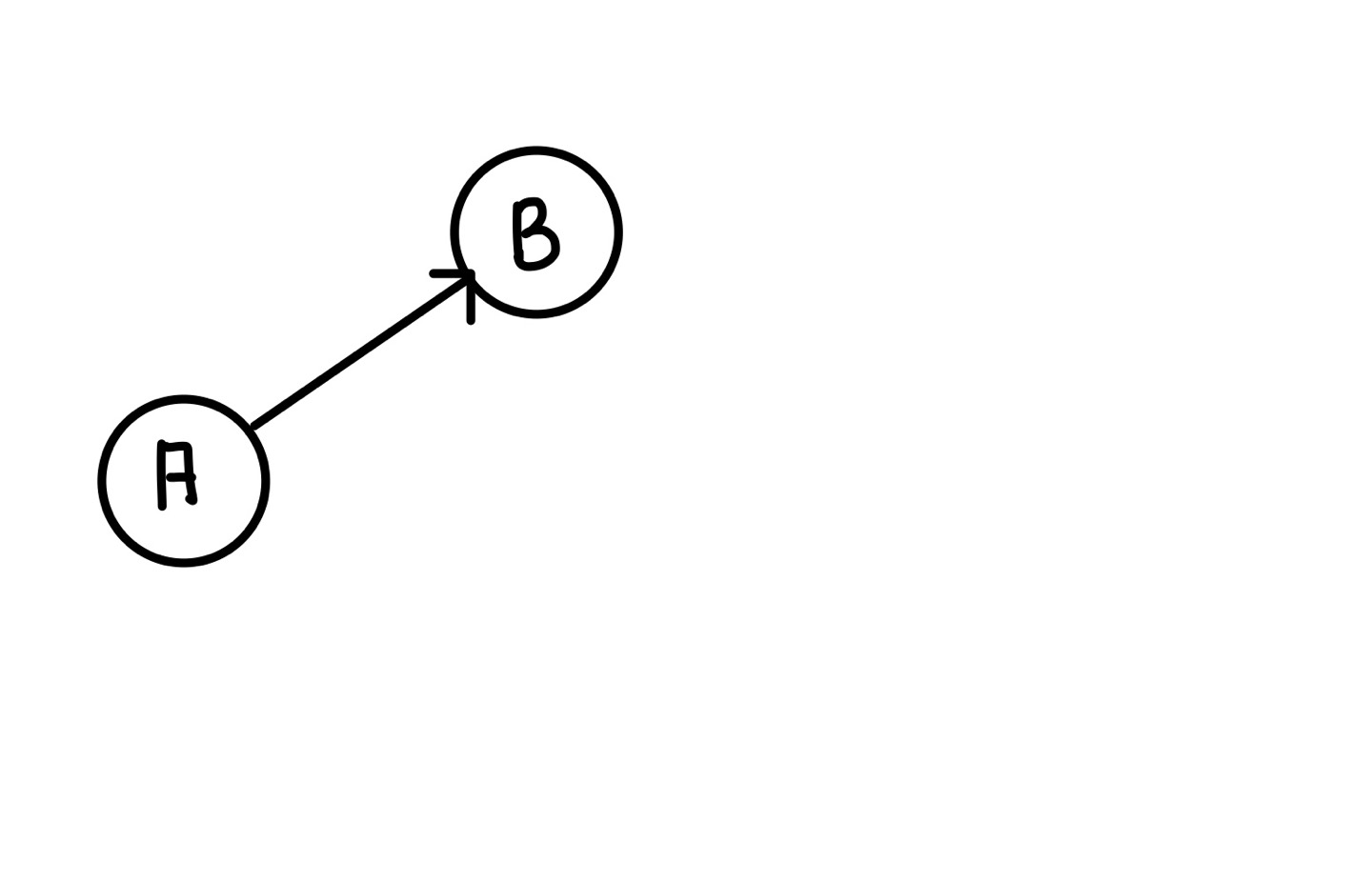
그 후 B는 C와 연결되어 있으므로 바로 C를 탐색한다.
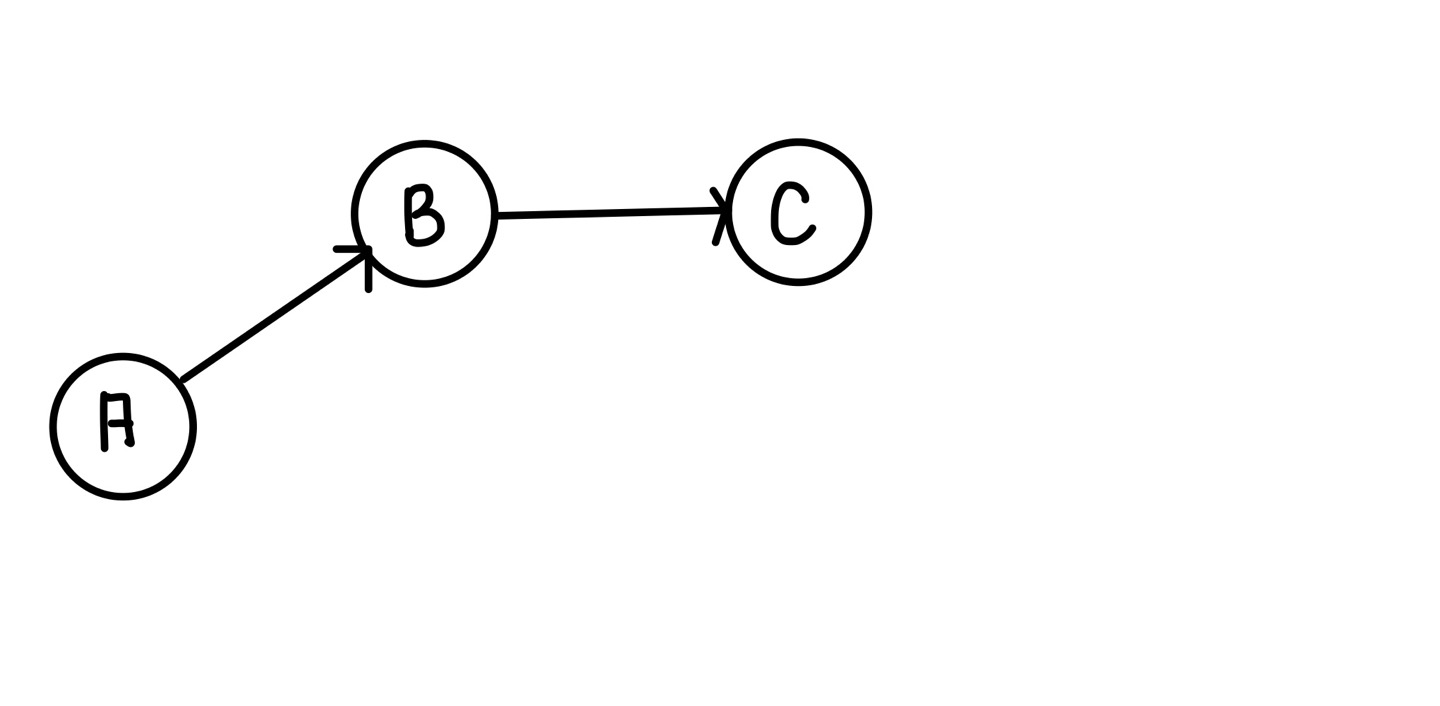
C 이후에는 연결된 것이 없으므로 다시 A로 돌아온다.
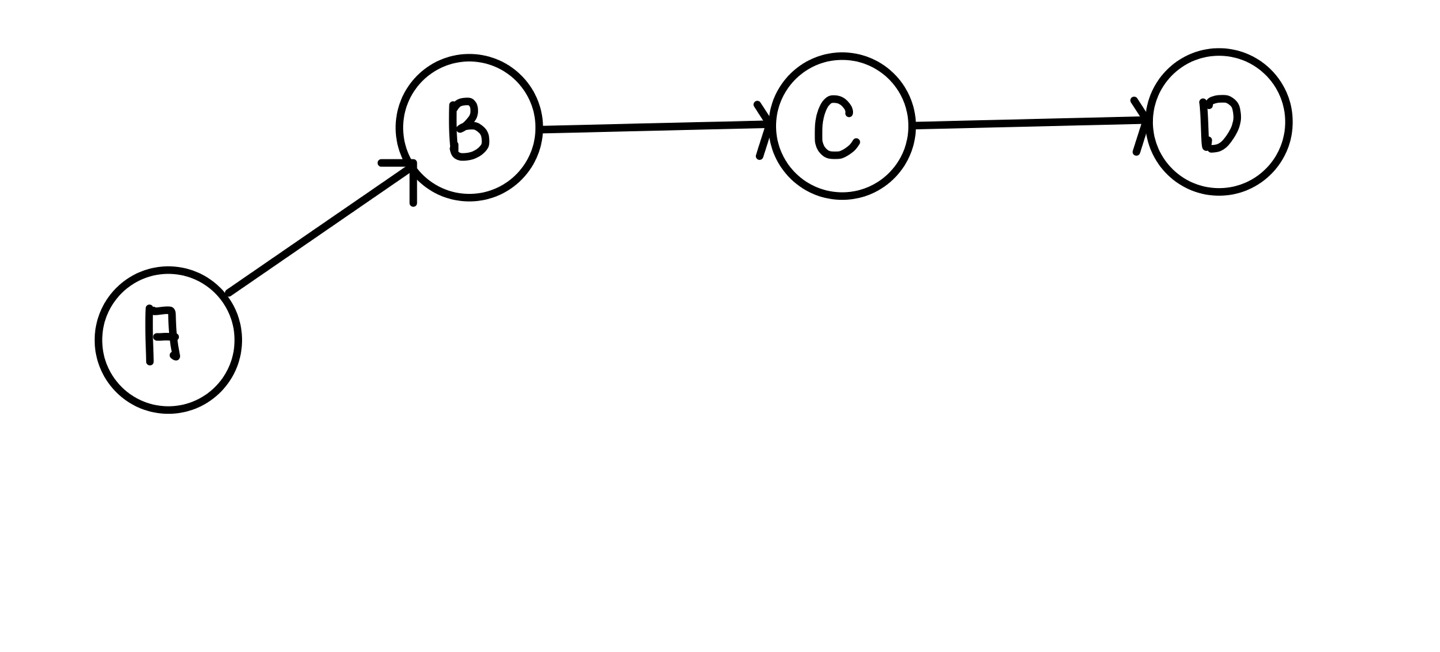
그 후 기존에 A에서 B를 탐색했으므로 나머지 경로인 E노드를 탐색하게 된다.
그 후 F노드를 탐색하게 되고 DFS탐색은 끝나게 된다.
다음은 탐색 순서를 입력해놓은 그림이다.
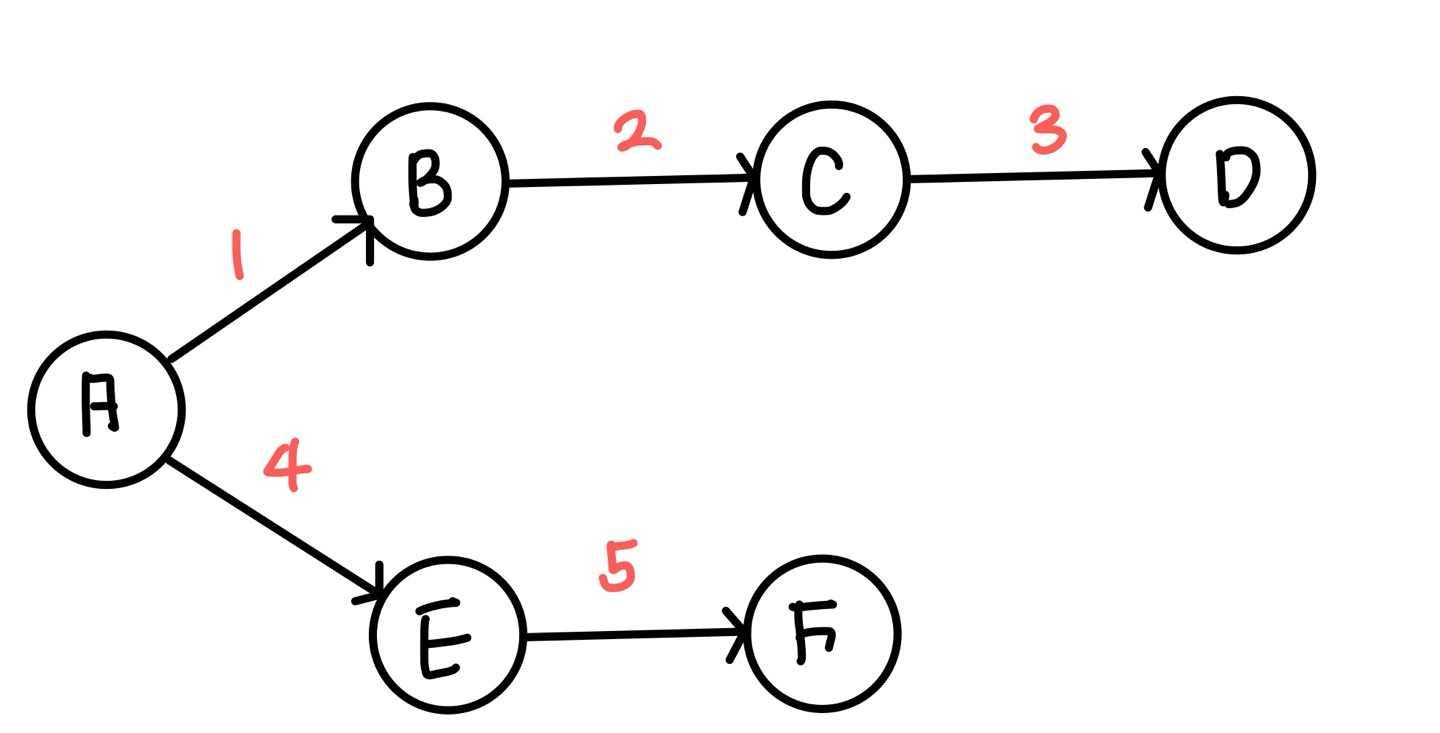
DFS탐색은 머리로는 어느정도 이해할 수 있다.
하지만 DFS는 정말 많이 쓰는 알고리즘중 하나이기 때문에 정확히 재귀가 어떻게 일어나는지 알고 가야한다.
위에서 본 그림은 우리가 보기 편하도록 사람의 입장에서 본 것이다.
다음은 컴퓨터 입장에서 본 DFS 작동 원리다.
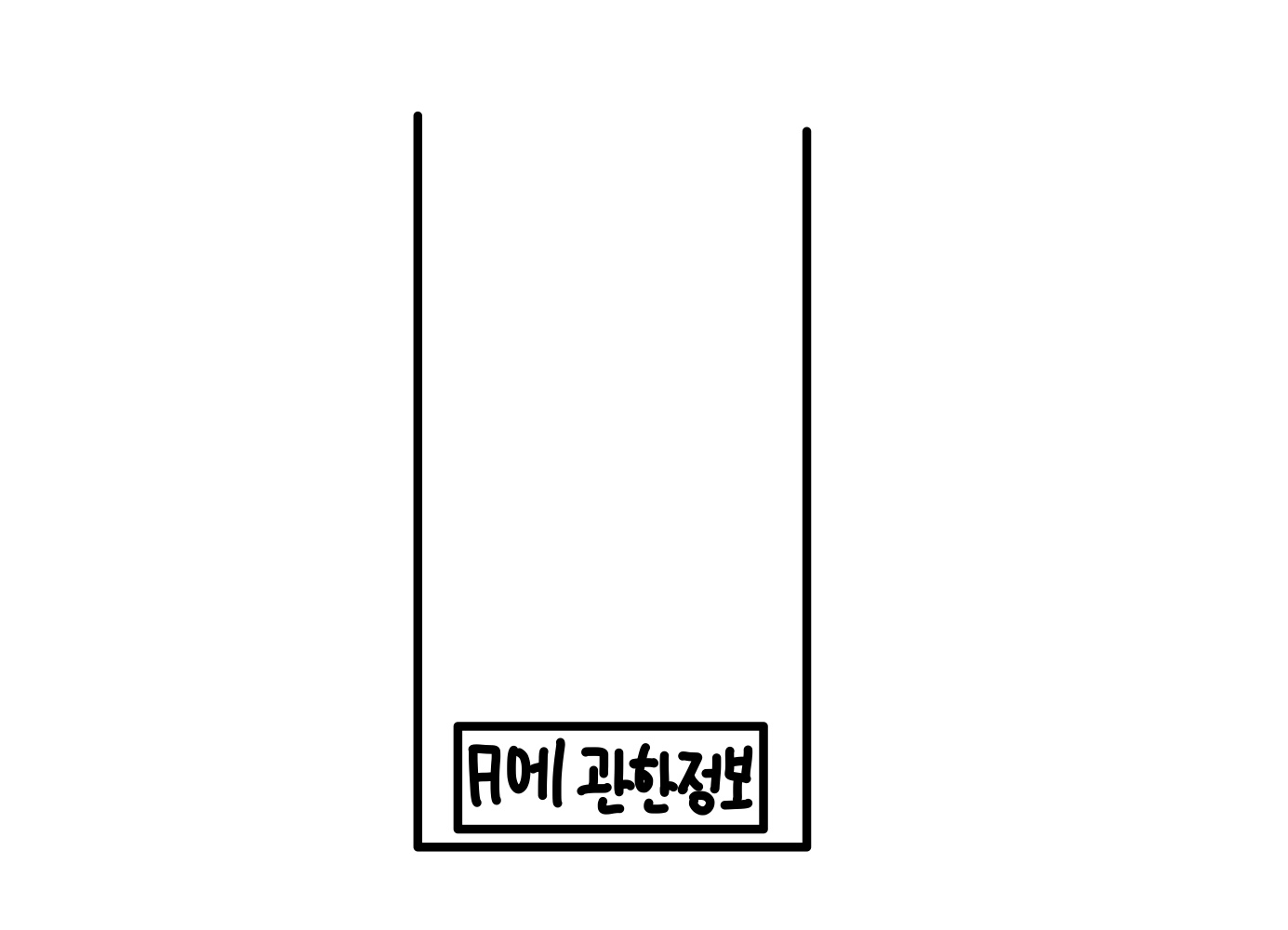
일단 컴퓨터는 스택처럼 들어간 정보를 저장해둔다.
이번 경우에는 A노드부터 시작했으므로 A에 관한 정보로 저장을 한다.
그 후 A에서 처음으로 들어가는 재귀부분인 B에 관한 정보가 저장된다.
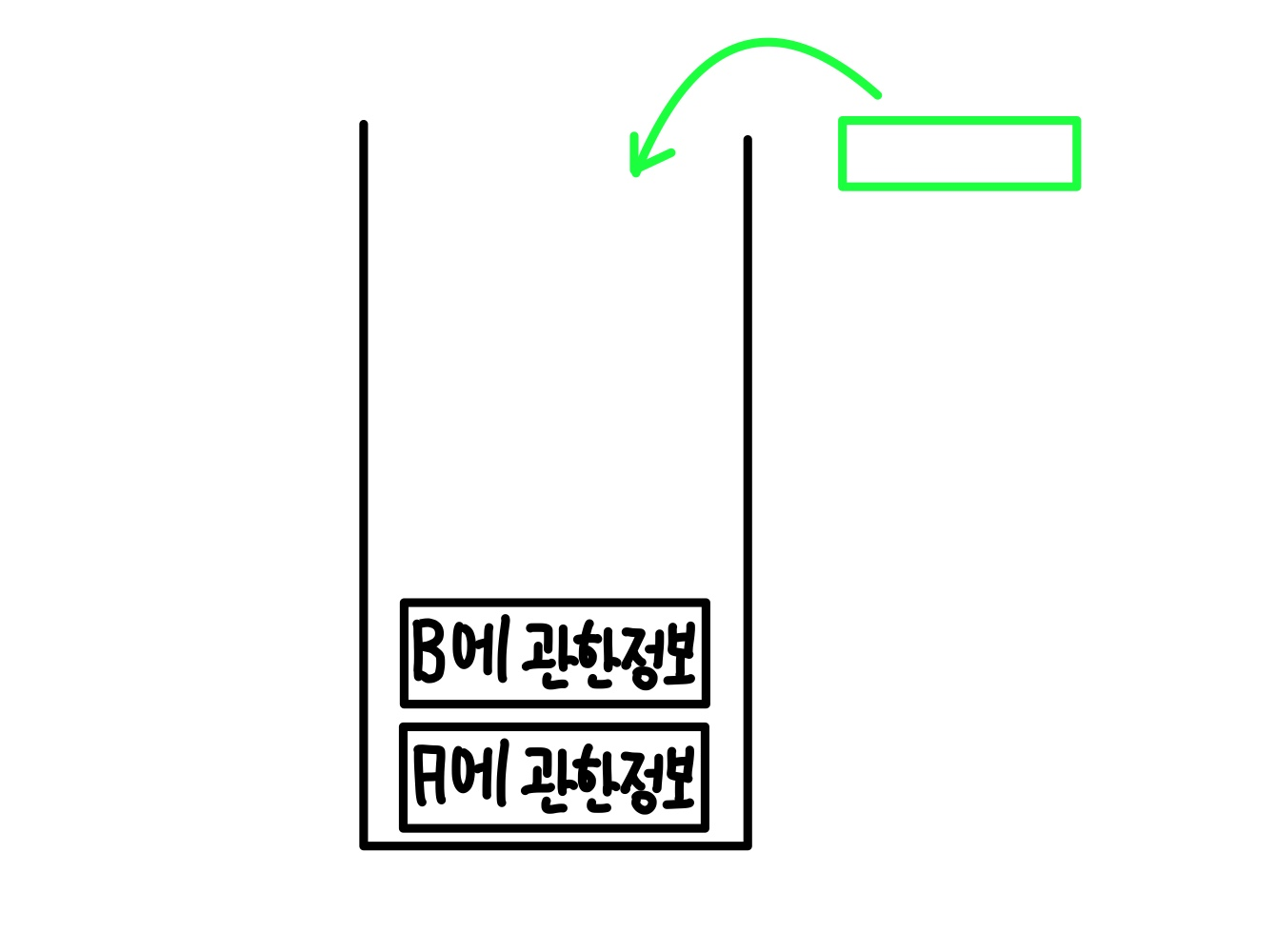
B에서는 C로 재귀함수가 작동하고
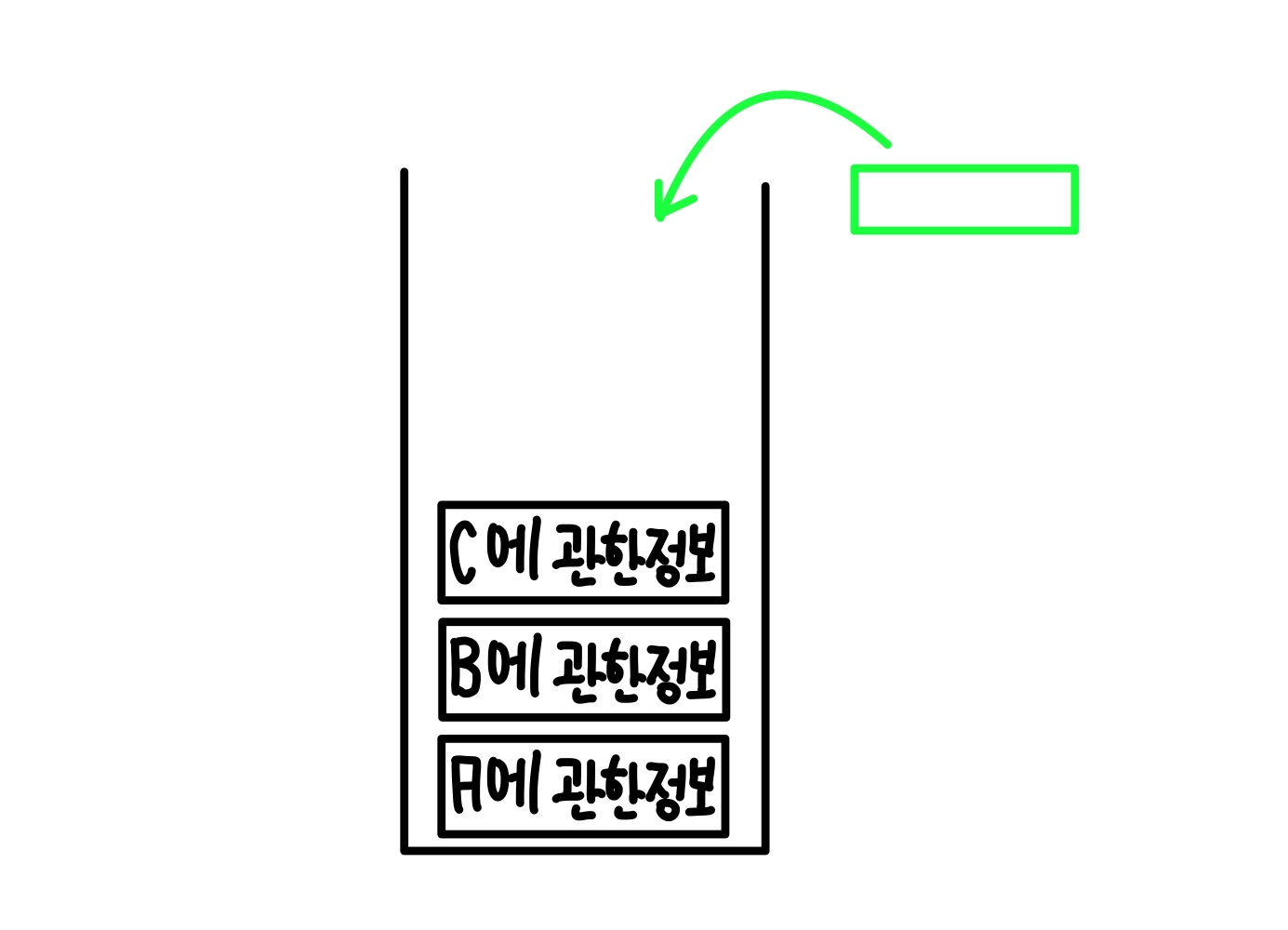
C에서는 D로 재귀함수가 작동한다.
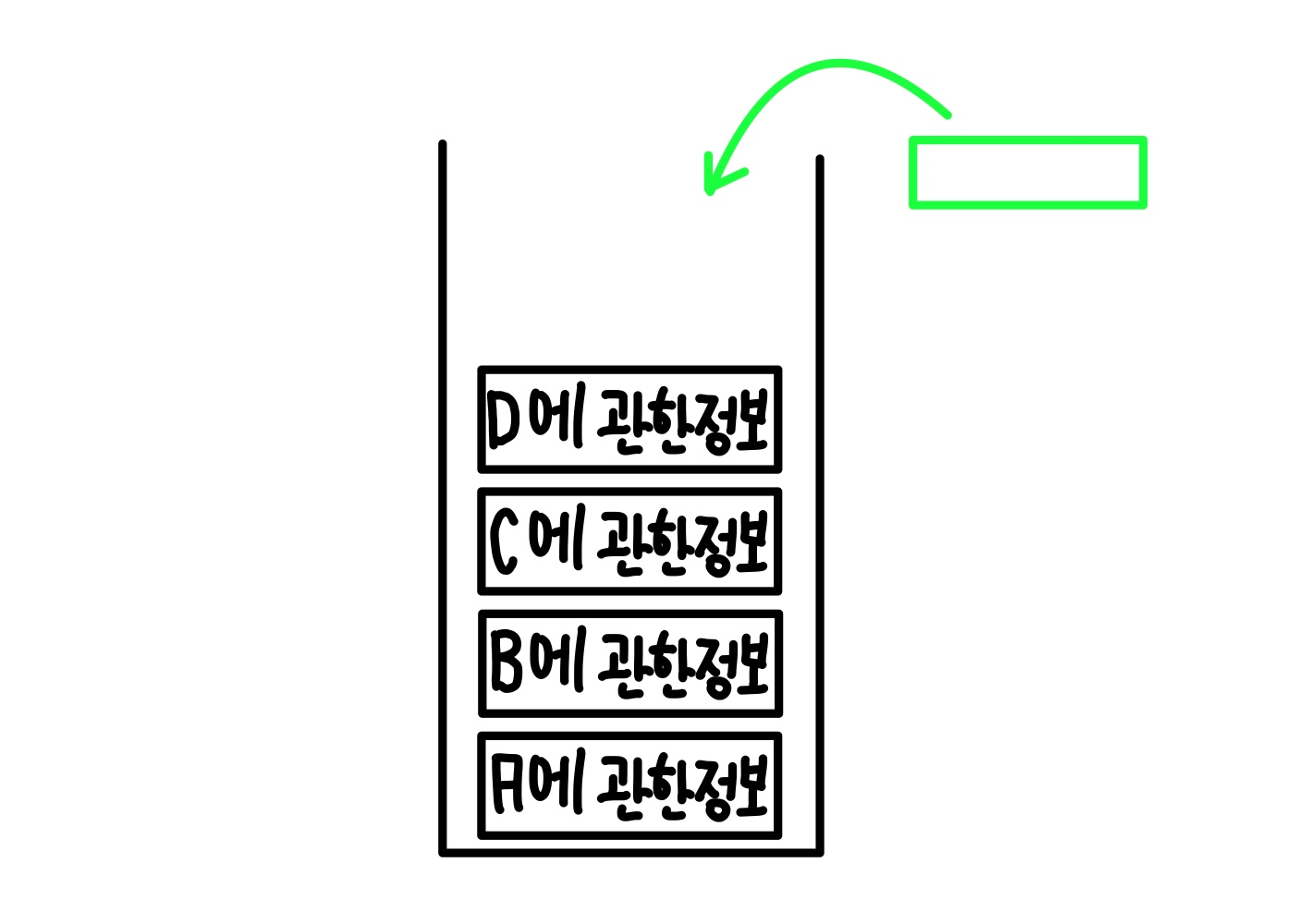
D에서는 더이상 작동할 재귀함수가 없으므로 D의 수행을 끝내고 저장된 데이터에서 제거를 한다.
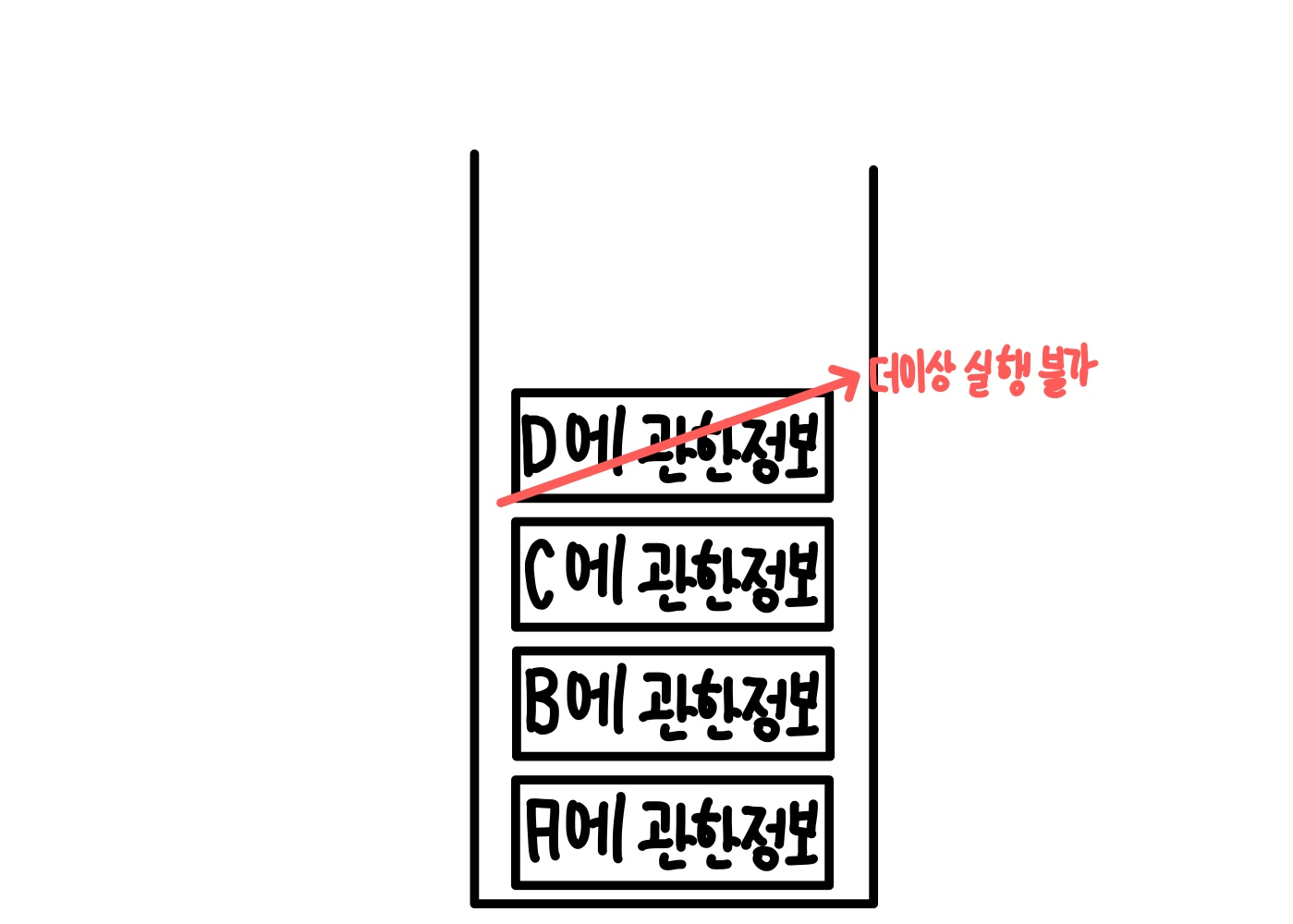
그리고 스택 형식으로 저장된 데이터중 가장 마지막으로 들어온 데이터를 실행한다.
이때 처음부터 실행하는 것이 아니라 기존에 실행하던 부분부터 실행하게 된다.
C는 사실상 D에 관한 정보를 불러오고 그 이후에는 실행 할 부분이 없으므로 끝나게 된다.
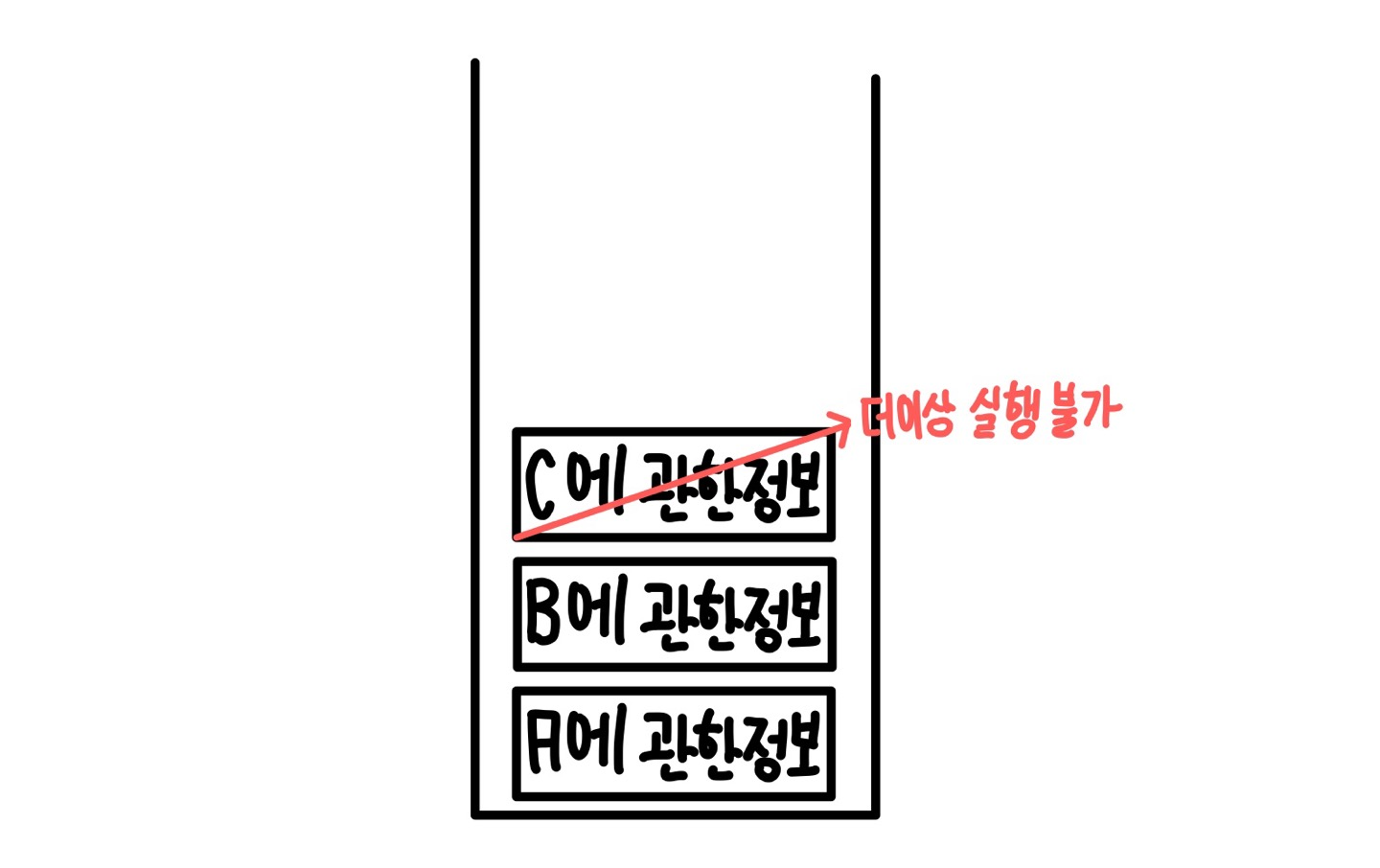
그 후 B도 마찬가지이다.
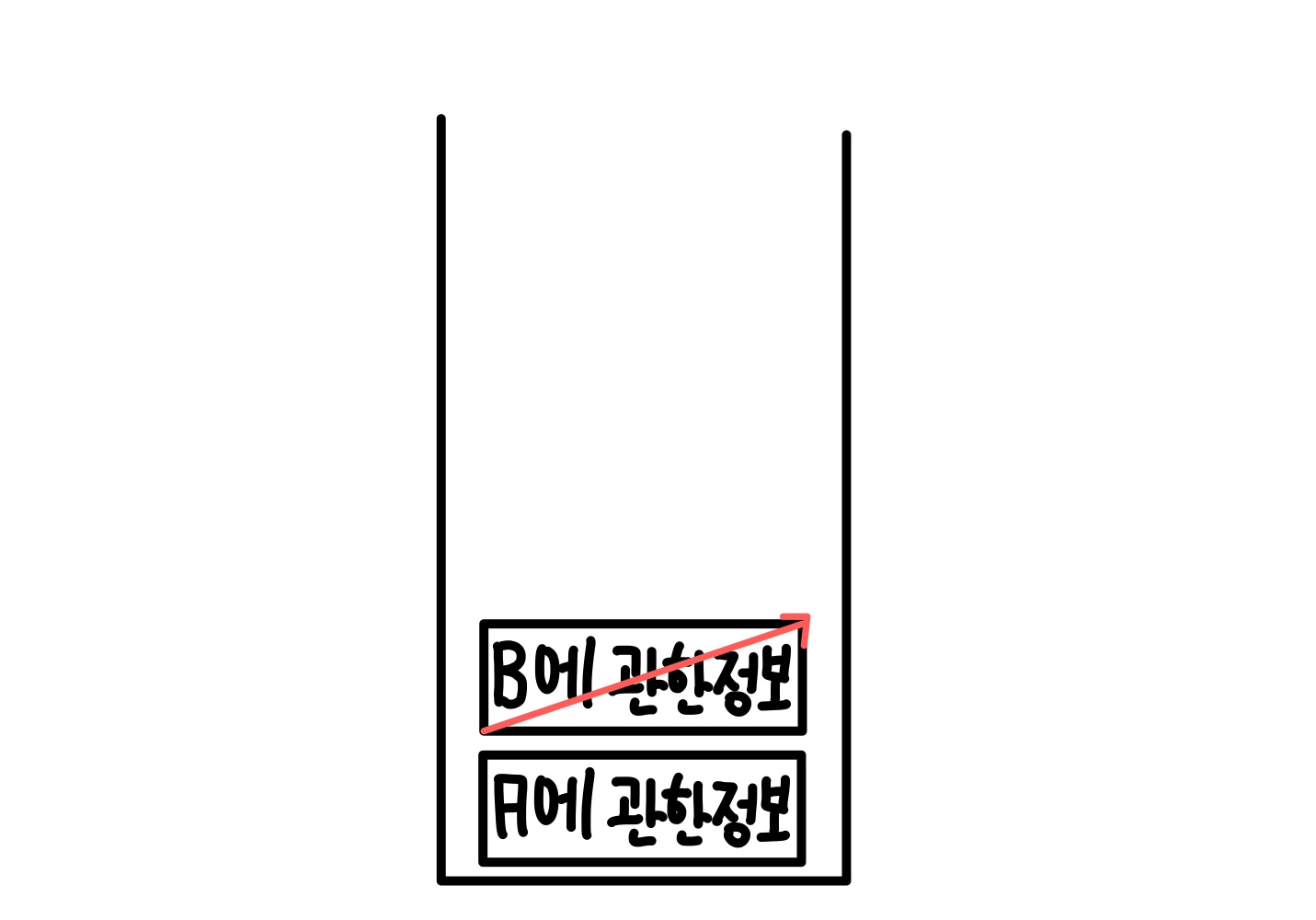
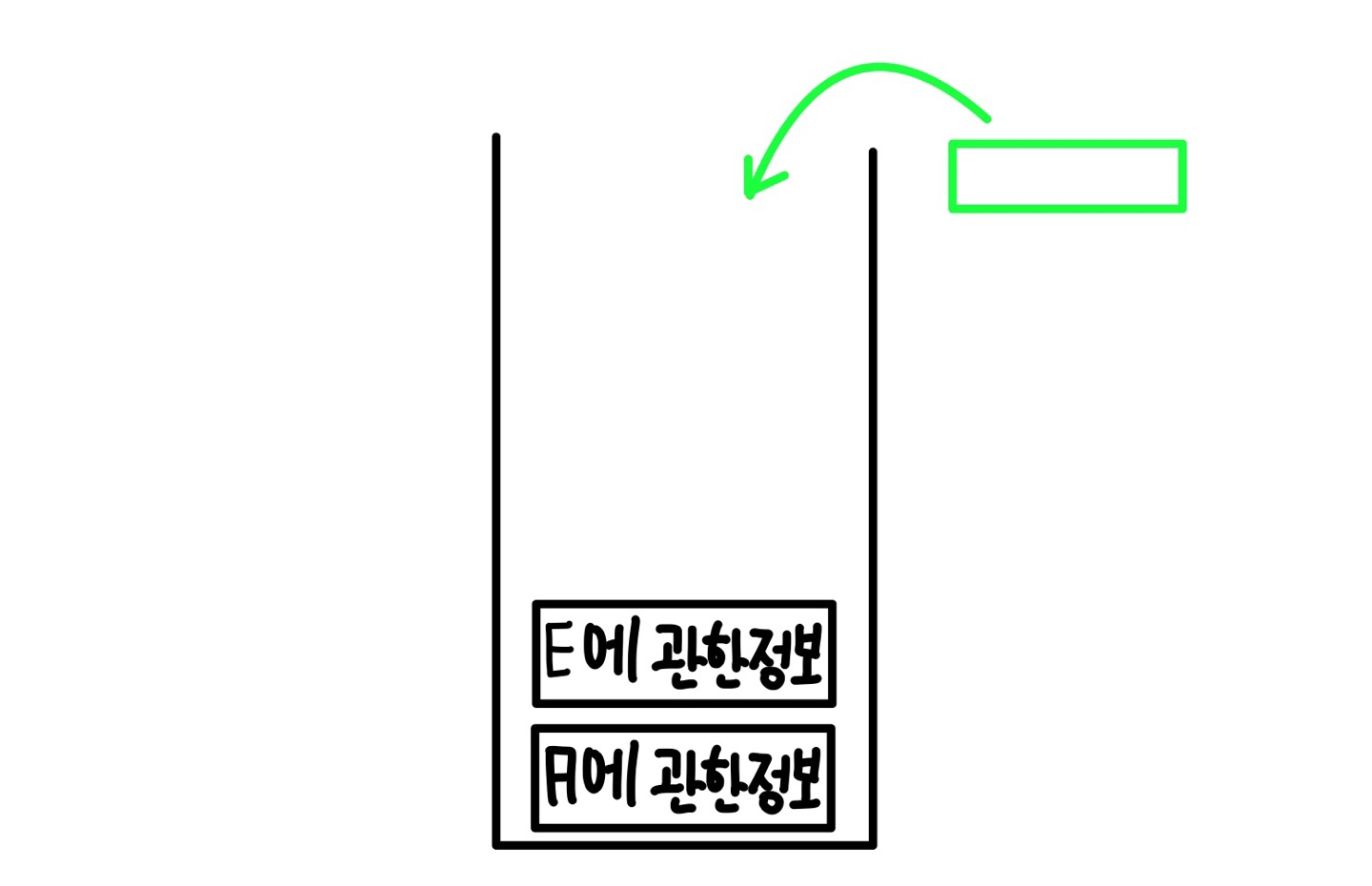
그러면 스택 저장소에는 A에 관한 정보만 남게 되는데 기존에 A는 B까지만 실행한 상태이고 그 다음으로 실행 할 부분이 있는지 확인해보니 E로 넘어가는 재귀가 존재하므로 실행하게 된다.
그 이후는 앞과 동일하다.
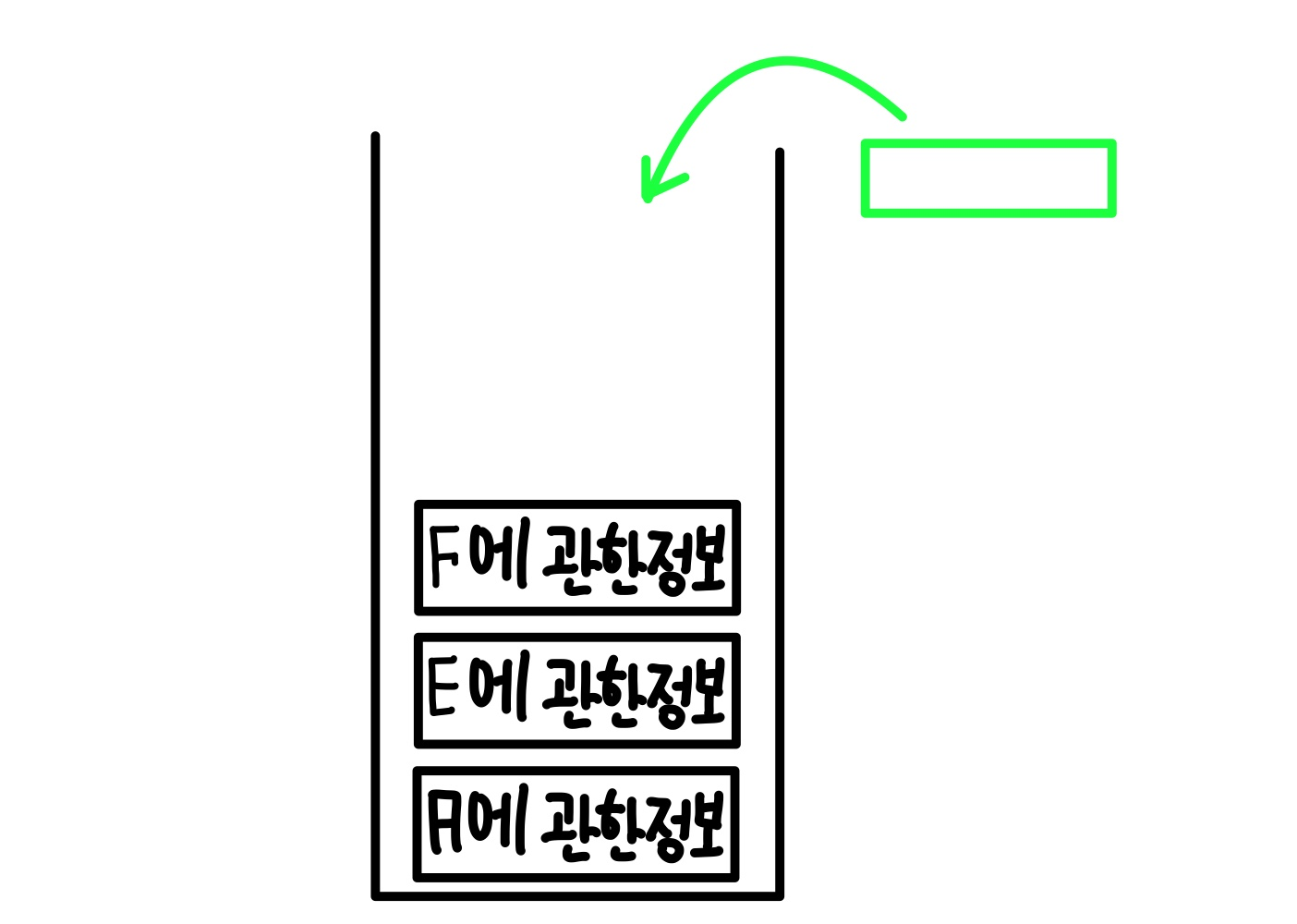
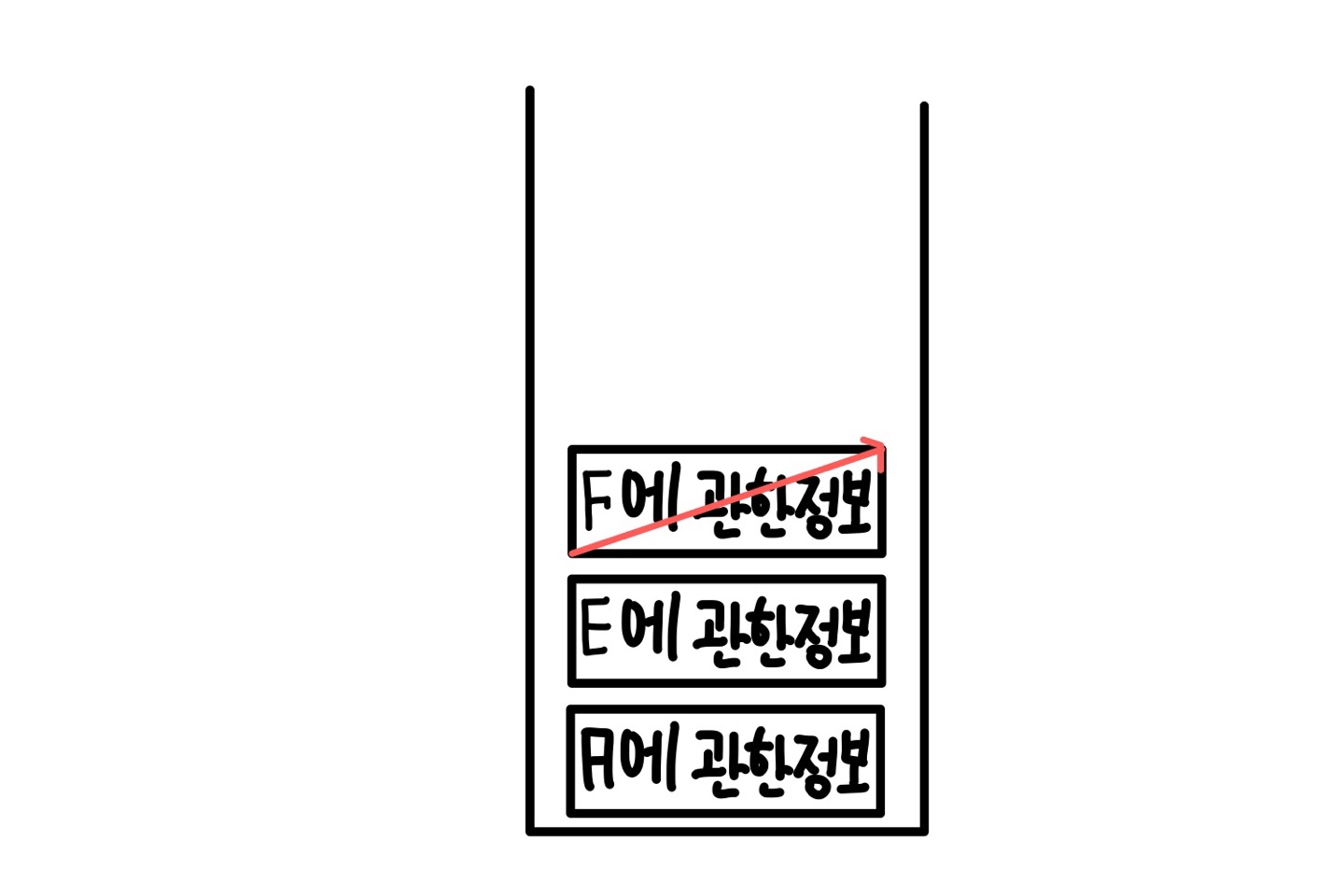
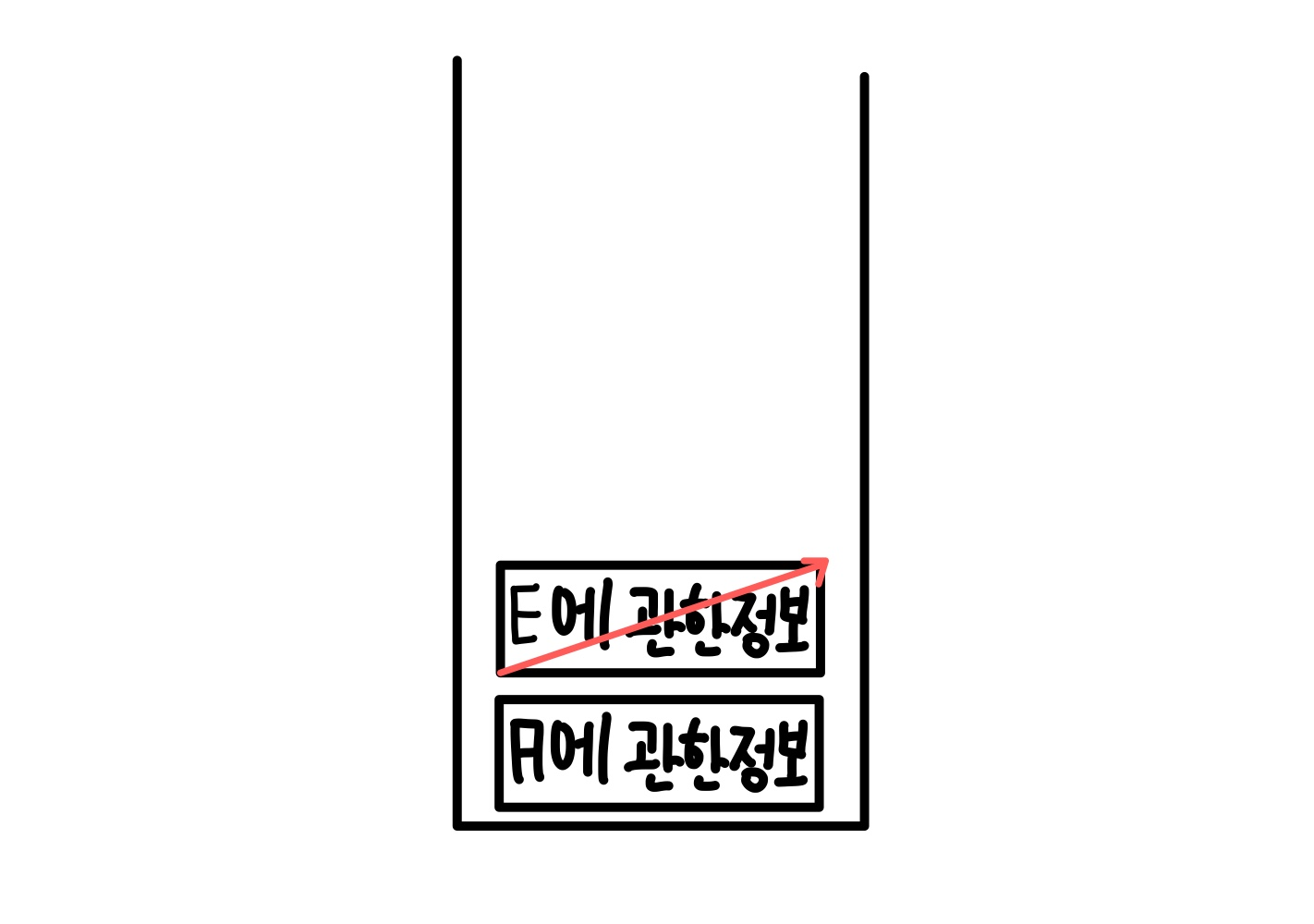
이렇게 마지막 부분까지 실행을 하고나면
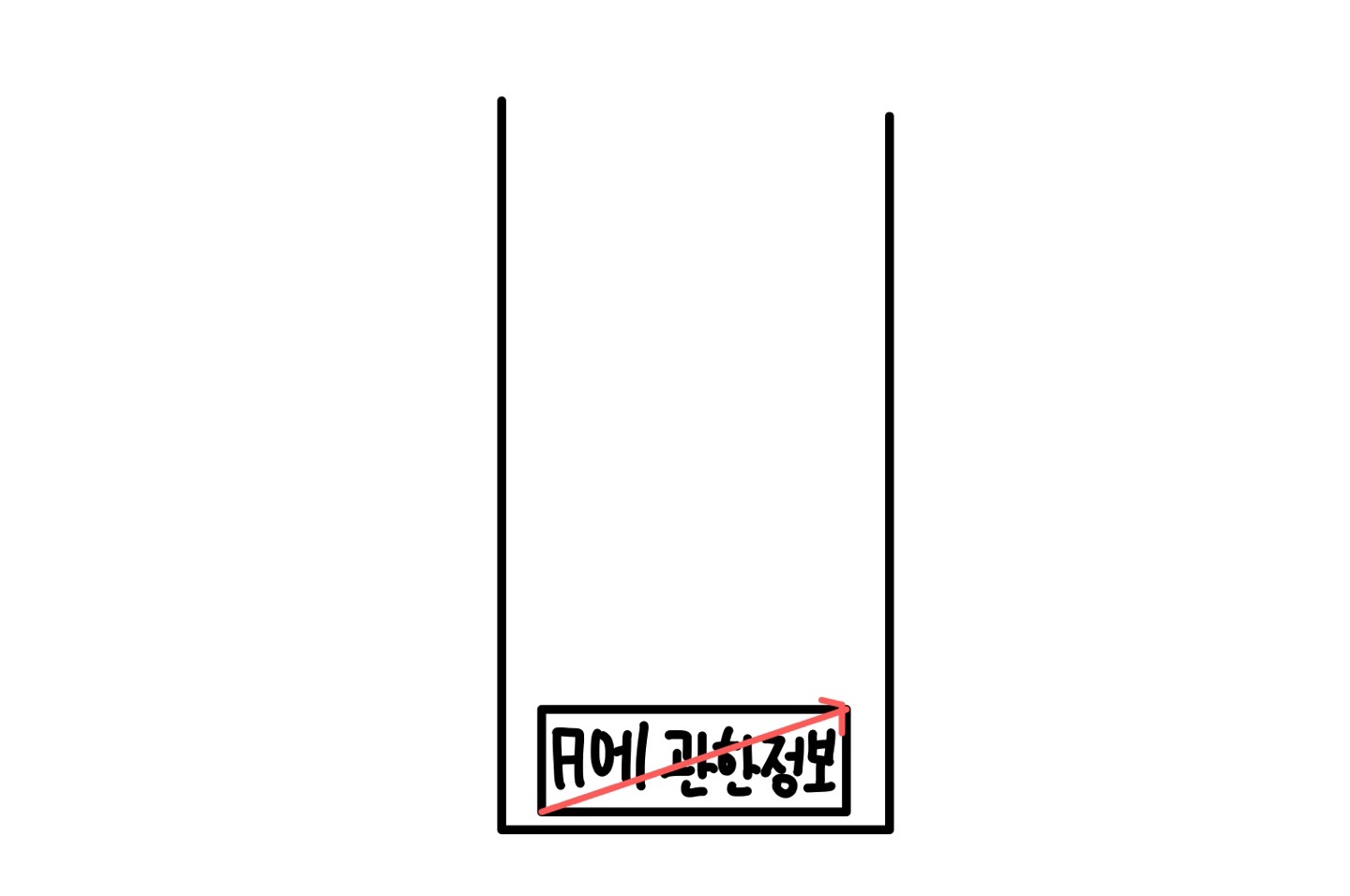
최종적으로 스택 저장소에는 아무것도 남게되지 않는다.
이러면 DFS탐색이 종료가 된다.
코드
# 그래프 만들기 각각 숫자에 대응되는 노드
# 1 -> A,2 -> B, 3 -> C, 4 -> D, 5 -> E, 6 -> F
# 각 행은 노드의 번호를 의미하며 행에 속해있는 데이터는 연결된 노드의 번호를 의미함.
graph = [[],
[2, 5],
[3],
[4],
[],
[6],
[]]
visited = [False for _ in range(7)] # 방문 확인하는 리스트
def DFS(start):
print('현재 방문 노드 {0}'.format(start))
for x in graph[start]:
if not visited[x]:
visited[x] = True
DFS(x)
DFS(1)느낀점
DFS를 처음에 공부할 때는 너무 어려웠는데 문제도 많이 풀어보고 이렇게 다시 복습도 해보니 익숙해진 것 같다.
DFS관련 문제는 많이 출제되는 편이니 열심히 공부해야겠다.